简介
一个公司有8个员工,每个员工有一个ID号(1B表示),员工的上班记录:
1.N个字节记录每个员工的情况
2.8bit记录员工的情况00101111(0表示上班)
优点:存储空间小,便于进行交叉运算(and,xor,or,not)
关键技术:压缩存储RLE
可以编码为0,8,2,11,1,2,3,11
其意思是:第一位为0,连续有8个,接下来是2个1,11个0,1个1,2个0,3个1,最后是11个0
应用
- 对数据进行快速地查找,判重,删除;(要求数据不重复)
- 去除重复数据达到压缩
1.对10亿个不重复的数据进行排序
假设用int表示一个数据,因为int为4字节,那么最多可以表示2^31-1即20亿的数据,满足题目10亿数据的要求,如果将这些数据按int存储,则需要的总空间为(10^9)*4/(1024*1024*1024)大概是4G左右,我们可以用bitmap来存储元素 "key,value"的形式
以“小端存储”为例,假设要存1,5,7,2,13
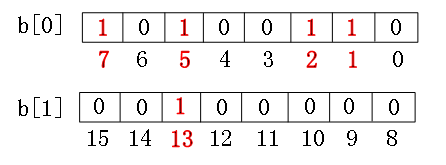
那么以前是4byte表示1位,现在是1bit表示1位,则实际需要的空间是4G/32不到0.1G左右,可以节约大量的内存空间
代码
下面介绍bitmap中的几种常见操作
1.clear 所有的bit置0
比如要将4置为,那么只需要构造出11101111,然后与b[0]求&操作即可。这可以将1左移4为,然后取反
假定要将数字i置为0
思路:
1.首先要确定i位于哪一个数组中
0~7 位于b[0]
8~15位于b[1]
16~23位于b[2]
…
可以推测i的数组下标为i/8,即index=i>>3
2.要计算i在当前8bit中的位置,即要求1应当左移几位
数字 位
0 0
1 1
2 2
…
7 7
8 0
9 1
10 2
总结:shift=i%8,即shift = i & 0x07;
3.置0
a[index] = a[index] & (~(1<<shift));
2.将某一位置为1,即存储
例如要存储4,构造出00010000,然后求或即可
1.首先找到数组的小标index
2.找到左移的位数shift
3.置1
3.判断当前位是否含1
仍然以4为例,只要与00010000求&,然后判断结果是否为0即可得知该位是否为1
4.输出排序后的结果
从0~10亿逐位判断是否为1
#include <iostream>
#include <limits>
using namespace std;
typedef unsigned char byte;
#define MAX_NUM 1000000000
byte a[MAX_NUM/8]; //数组大小
//找到数组的下标
int get_index(int i)
{
return i>>3;//即i/8
}
//找到位移的次数
int get_shift(int i)
{
return i & 0x07;//即i%8
}
void clear(int i)
{
int index= get_index(i);
int shift = get_shift(i);
//置0
a[index] &= (byte)(~(1<<shift));
}
void set(int i)
{
int index= get_index(i);
int shift = get_shift(i);
a[index] |= ((byte)(1<<shift));
}
void clear_all(int max_num=MAX_NUM)
{
for(int i=0;i<=max_num;i++)
clear(i);
}
void bit_map(int array[], int size,int max_num=MAX_NUM)
{
clear_all(max_num);
for(int i=0;i<size;i++)
{
set(array[i]);
}
}
//返回1,表示存在
int contain(int i)
{
int index= get_index(i);
int shift = get_shift(i);
int exist = a[index] &(1<<shift);
return exist;
}
void print(int max_num)
{
for(int i=0;i<=max_num;i++)
{
if(contain(i))
cout<<i<<' ';
}
cout<<endl;
}
int main()
{
int m[]={21,25,10,12,14};
int size=5;
bit_map(m,size,21);
print(21);
return 0;
}http://blog.csdn.net/hguisu/article/details/7880288
http://www.infoq.com/cn/articles/the-secret-of-bitmap








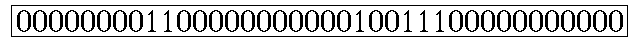














 312
312

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








