字符串全排列算法理解与java实现

字符串全排列算法问题描述：输入一个字符串，打印出该字符串中字符的所有排列。例如输入字符串abc，则输出由字符a，b，c所能排列出来的所有字符串abc，acb，bac，bca，cab和cba

解题思路（这部分参考http://www.cnblogs.com/cxjchen/p/3932949.html）：

如果能生成n-1个元素的全排列，就能生成n个元素的全排列。对于只有一个元素的集合，可以直接生成全排列。所以全排列的递归终止条件很明确，只有一个元素时。我们可以分析一下全排列的过程：

1. 首先，我们固定第一个字符a，求后面两个字符bc的排列
2. 当两个字符bc排列求好之后，我们把第一个字符a和后面的b交换，得到bac，接着我们固定第一个字符b，求后面两个字符ac的排列
3. 现在是把c放在第一个位置的时候了，但是记住前面我们已经把原先的第一个字符a和后面的b做了交换，为了保证这次c仍是和原先处在第一个位置的a交换，我们在拿c和第一个字符交换之前，先要把b和a交换回来。在交换b和a之后，再拿c和处于第一位置的a进行交换，得到cba。我们再次固定第一个字符c，求后面两个字符b、a的排列
4. 既然我们已经知道怎么求三个字符的排列，那么固定第一个字符之后求后面两个字符的排列，就是典型的递归思路了

下面这张图很清楚的给出了递归的过程：

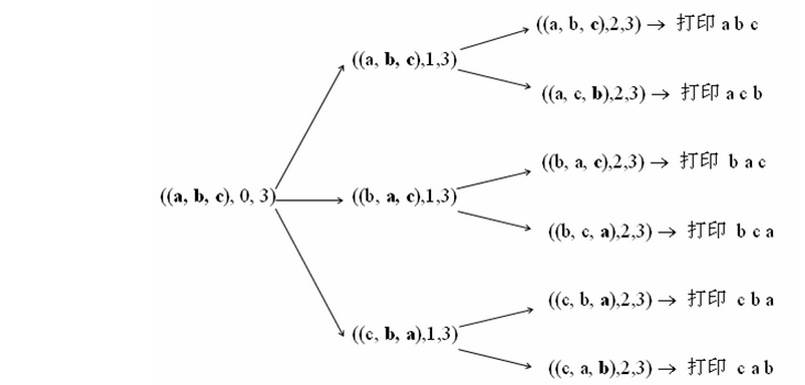
递归的出口，就是只剩一个字符的时候，递归的循环过程，就是从每个子串的第二个字符开始依次与第一个字符交换，然后继续处理子串。

另外，还有一个要注意的问题就是存在重复字符。

由于全排列就是从第一个数字起，每个数分别与它后面的数字交换，我们先尝试加个这样的判断——如果一个数与后面的数字相同那么这两个数就不交换了。例如abb，第一个数与后面两个数交换得bab，bba。然后abb中第二个数和第三个数相同，就不用交换了。但是对bab，第二个数和第三个数不同，则需要交换，得到bba。由于这里的bba和开始第一个数与第三个数交换的结果相同了，因此这个方法不行。

换种思维，对abb，第一个数a与第二个数b交换得到bab，然后考虑第一个数与第三个数交换，此时由于第三个数等于第二个数，所以第一个数就不再用与第三个数交换了。再考虑bab，它的第二个数与第三个数交换可以解决bba。此时全排列生成完毕！

这样，我们得到在全排列中去掉重复的规则：

去重的全排列就是从第一个数字起，每个数分别与它后面非重复出现的数字交换。

算法实现：

import java.util.Scanner;
 
public class Demo001 {
     
    public static void main(String[] args) {
        String str = "";
         
        Scanner scan = new Scanner(System.in);
         
        str = scan.nextLine();
         
        permutation(str.toCharArray(), 0);
    }
 
    public static void permutation(char[] str, int i) {
        if (i >= str.length||i<0)
            return;
        if (i == str.length - 1) {
            System.out.println(String.valueOf(str));//记录字符串
        } else {
            for (int j = i; j < str.length; j++) {
                if(is_swap(str,i,j)){
                swap(str,i,j);
                permutation(str, i + 1);
                swap(str,i,j);
                }
 
            }
        }
    }
    
    //判断从子串的第一个字符串开始，直到j-1位置，看是否有重复的字符，若有重复字符，则不再交换
    public static boolean is_swap(char[] str,int begin,int j){
       for(int k=begin;k<j;k++){
         if(str[k] == str[j]){
           return false;
          }
       }
           return true;
    }
    
    //两个字母进行交换
    public static void swap(char[] str,int i,int j){
        char temp = str[j];
        str[j] = str[i];
        str[i] = temp;
    }
 
}