KMP算法初探

最新推荐文章于 2021-07-31 17:59:26 发布

奋斗的鱼

最新推荐文章于 2021-07-31 17:59:26 发布

阅读量454

点赞数

分类专栏：数据结构与算法

本文链接：https://blog.csdn.net/jbfsdzpp/article/details/48844975

版权

数据结构与算法专栏收录该内容

30 篇文章 0 订阅

订阅专栏

关于字符串的算法，很早就知道KMP算法，但是一直没有理解，正好这个假期没多少事，可以好好琢磨一下这个算法。下面结合一道题目来说明KMP算法要解决的问题。

【题目】
给定两个字符串str和match，长度分别为N和M。实现一个算法，如果字符串str中含有字串match，则返回match在str中的开始位置，不含有则返回-1。
【举例】
str=“acbc”，match=“bc”。返回2。
str=“acbc”，match=“bcc”。返回-1。
【要求】
如果match的长度大于str长度(M>N)，str必然不会含有match，可直接返回-1。但如果N>=M，要求算法复杂度O(N)。

这个题目很好理解，就是字符串的匹配，首先可以想到的就是从头开始比较两个字符是否相等，不相等就从N的下一个字符开始比较就可以了，这个思路没有错，它就是最朴素的BF（Brute-Force,最基本的字符串匹配算法）。

一：BF算法简介

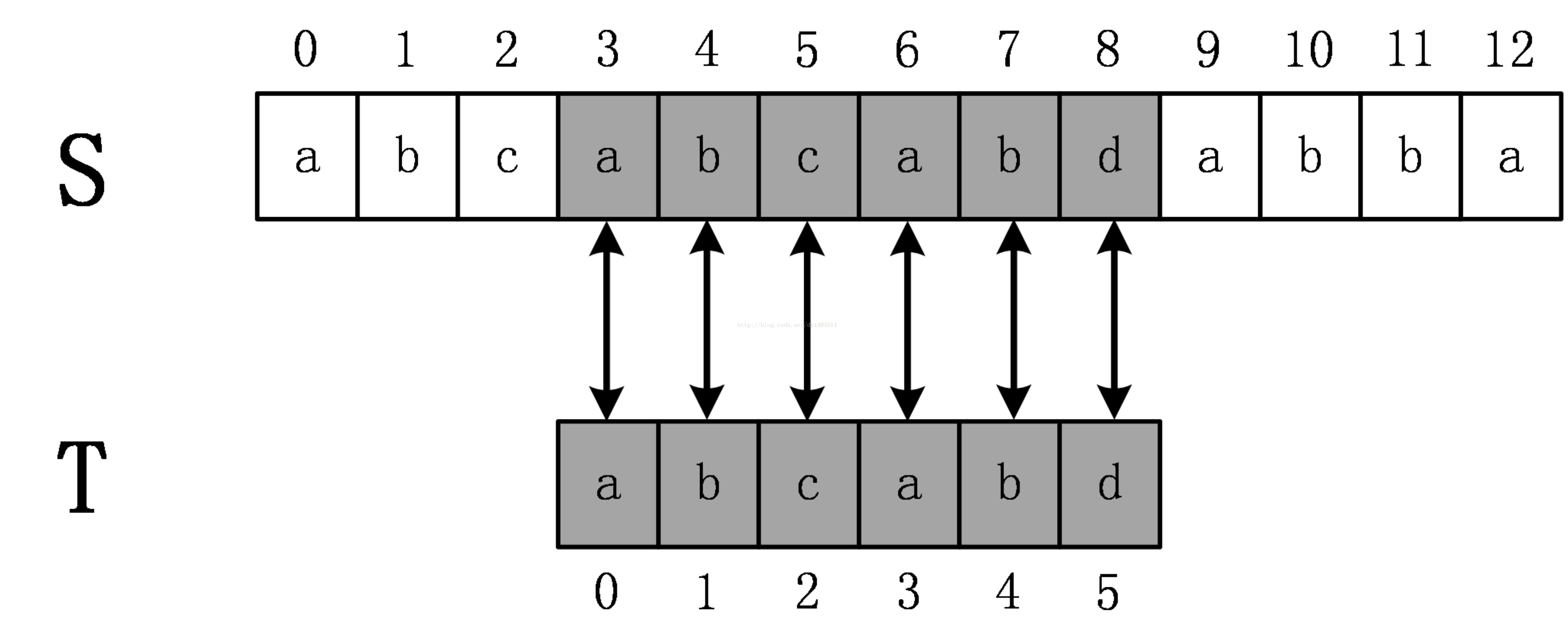
如上图所示，原始串S=abcabcabdabba,模式串为abcabd。（下标从0开始）从s[0]开始依次比较S[i] 和T[i]是否相等，直到T[5]时发现不相等,这时候说明发生了失配，在BF算法中，发生失配时，T必须回溯到最开始，S下标+1，然后继续匹配，如下图所示：

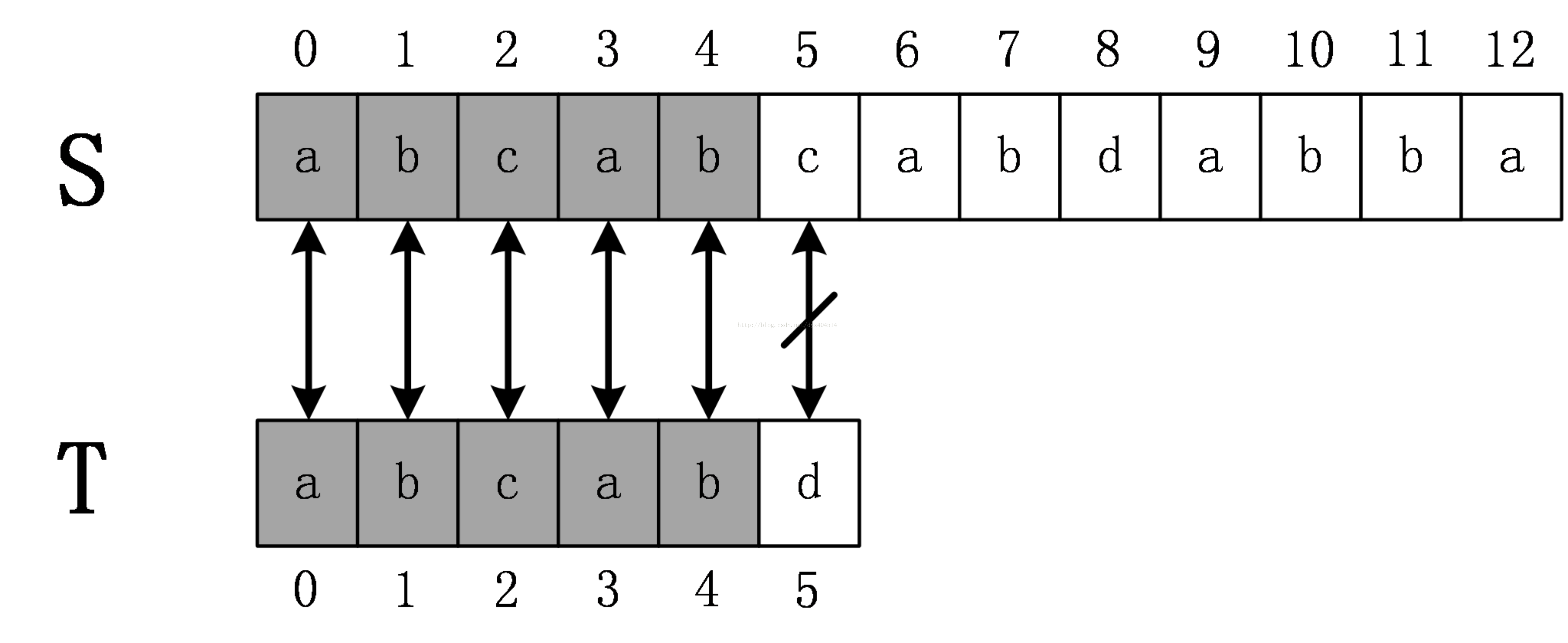
这次立即发生了失配，所以继续回溯，直到S开始下表增加到3，匹配成功。

容易得到，BF算法的时间复杂度是O(n*m)的，其中n为原始串的长度，m为模式串的长度。

二：KMP算法

前面提到了朴素匹配算法，它的优点就是简单明了，缺点当然就是时间消耗很大。KMP算法是对BF算法的改进，它的主要思想就是：在匹配匹配过程中发生失配时，并不简单的从原始串下一个字符开始重新匹配，而是根据一些匹配过程中得到的信息跳过不必要的匹配，从而达到一个较高的匹配效率。

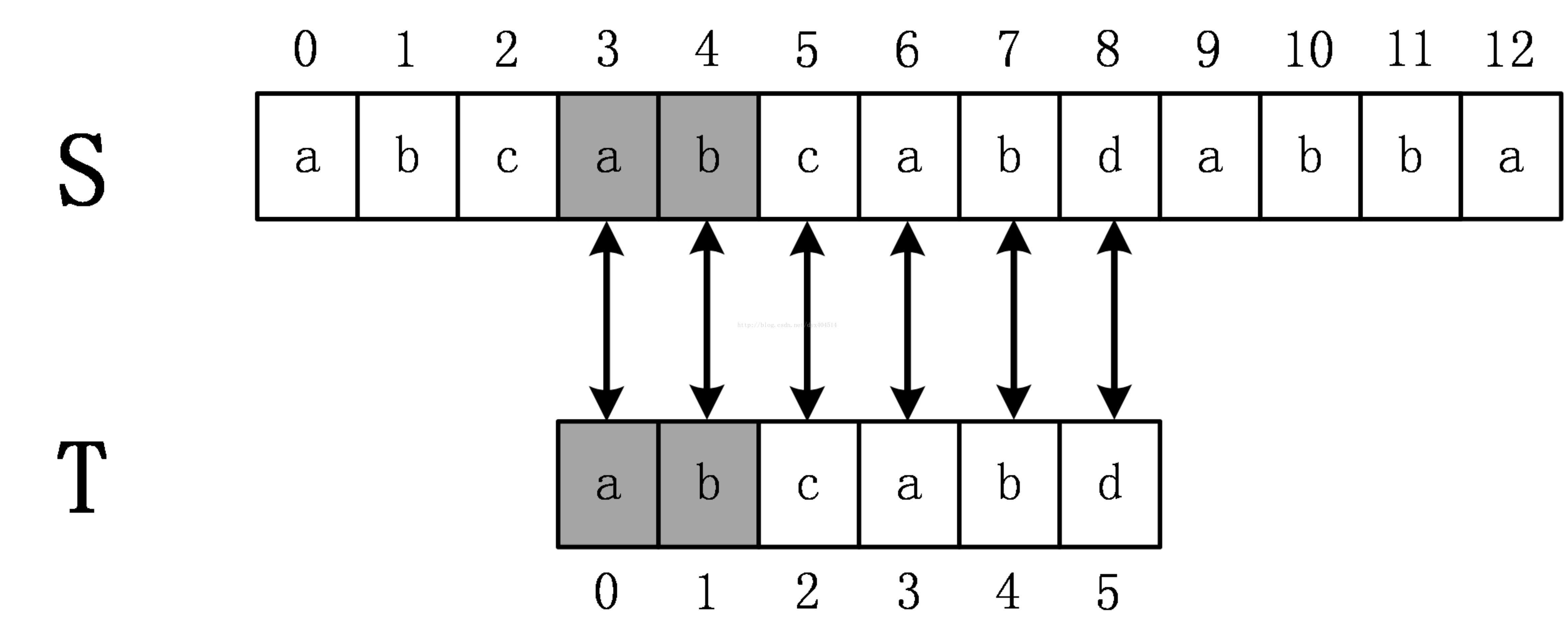
还是前面的例子，原始串S=abcabcabdabba,模式串为abcabd。当第一次匹配到T[5]!=S[5]时，KMP算法将T向右移动3位，这个位数是怎么计算的呢？这就需要用到KMP算法中非常重要的一个东西：next数组（也叫fail数组，前缀数组），其实质是对模式串进行预处理。next数组的具体计算我们后面再说，现在直接给出失配字符d的前一个字符的next数组值，是2，模式串移动的位数的计算公式为：移动位数 = 已匹配的字符数 - 对应的部分匹配值。该例中移动位数为5-2=3。移动后的匹配过程如下，若出现不匹配，继续循环这个过程，直到完全匹配。

下面介绍next数组，next数组的值表示该字符的前缀和后缀的最长共有元素的长度。

首先，要了解两个概念："前缀"和"后缀"。 "前缀"指除了最后一个字符以外，一个字符串的全部头部组合；"后缀"指除了第一个字符以外，一个字符串的全部尾部组合。

　　以"ABCDABD"为例，求"前缀"和"后缀"的最长的共有元素的长度：

　　－　"A"的前缀和后缀都为空集，共有元素的长度为0；

　　－　"AB"的前缀为[A]，后缀为[B]，共有元素的长度为0；

　　－　"ABC"的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度0；

　　－　"ABCD"的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，共有元素的长度为0；

　　－　"ABCDA"的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为"A"，长度为1；

　　－　"ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为"AB"，长度为2；

　　－　"ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的长度为0。

接下来介绍next数组的计算：

设模式串T[0,m-1],长度为m，由next数组的定义，可知next[0]=next[1]=0，（因为这里的串的后缀，前缀不包括该串本身）。

接下来，假设我们从左到右依次计算next数组，在某一时刻，已经得到了next[0]~next[i],现在要计算next[i+1]，设j=next[i]，由于知道了next[i]，所以我们知道T[0,j-1]=T[i-j,i-1],现在比较T[j]和T[i]，如果相等，由next数组的定义，可以直接得出next[i+1]=j+1。

如果不相等，那么我们知道next[i+1]<j+1，所以要将j减小到一个合适的位置po，使得po满足:

1）T[0,po-1]=T[i-po,i-1]。

2）T[po]=T[i]。

3）po是满足条件(1),(2)的最大值。

4）0<=po<j（显然成立）。

如何求得这个po值呢？事实上，并不能直接求出po值，只能一步一步接近这个po，寻找当前位置j的下一个可能位置。如果只要满足条件(1)，那么j就是一个，那么下一个满足条件(1)的位置是什么呢？，由next数组的定义，容易得到是next[j]=k，这时候只要判断一下T[k]是否等于T[i]，即可判断是否满足条件(2),如果还不相等，继续减小到next[k]再判断，直到找到一个位置P,使得P同时满足条件(1)和条件(2)。我们可以得到P一定是满足条件(1),(2)的最大值，因为如果存在一个位置x使得满足条件(1),(2),(4)并且x>po,那么在回溯到P之前就能找到位置x，否则和next数组的定义不符。在得到位置po之后，容易得到next[i+1]=po+1。那么next[i+1]就计算完毕，由数学归纳法，可知我们可以求的所有的next[i]。(0<=i<m)

注意：在回溯过程中可能有一种情况,就是找不到合适的po满足上述4个条件，这说明T[0,i]的最长前后缀串长度为0，直接将next[i+1]赋值为0,即可。】

 public int[] getNextArray(char[] ms) { 
        if (ms.length == 1) { 
            return new int[] { 0 }; 
        } 
        int[] next = new int[ms.length]; 
        next[0]=next[1]=0;//初始化  
        for(int i=1;i<len;i++)  
        {  
            int j=next[i];  
            while(j&&str[i]!=str[j])//一直回溯j直到str[i]==str[j]或j减小到0  
            j=next[j];  
            next[i+1]=str[i]==str[j]?j+1:0;//更新next[i+1]
        }
        return next;
 }

有了next数组，我们就可以通过next数组跳过不必要的检测，加快字符串匹配的速度了。那么为什么通过next数组可以保证匹配不会漏掉可匹配的位置呢？

首先，假设发生失配时T的下标在i，那么表示T[0,i-1]与原始串S[l,r]匹配,设next[i]=j，根据KMP算法，可以知道要将T回溯到下标j再继续进行匹配，根据next[i]的定义，可以得到T[0,j-1]和S[r-j+1,r]匹配，同时可知对于任何j<y<i，T[0,y]不和S[r-y,r]匹配，这样就可以保证匹配过程中不会漏掉可匹配的位置。

同next数组的计算，在一般情况下，可能回溯到next[i]后再次发生失配，这时只要继续回溯到next[j]，如果不行再继续回溯，最后回溯到next[0]，如果还不匹配，这时说明原始串的当前位置和T的开始位置不同，只要将原始串的当前位置+1，继续匹配即可。

下面给出KMP算法匹配过程的代码:

  public int getIndexOf(String s, String m) { 
        if (s == null || m == null || m.length() < 1 || s.length() < m.length()) { 
        return -1; 
        } 
        char[] ss = s.toCharArray(); 
        char[] ms = m.toCharArray(); 
        int si = 0; 
        int mi = 0; 
        int[] next = getNextArray(ms); 
        while (si < ss.length && mi < ms.length) { 
        if (ss[si] == ms[mi]) { 
            si++; 
            mi++; 
        } else if (next[mi] == -1) { 
            si++; 
        } else { 
            mi = next[mi]; 
        } 
        } 
        return mi == ms.length ? si - mi : -1; 
    }

前面说到，KMP算法的时间复杂度是线性的，但这从代码中并不容易得到，很多读者可能会想，如果每次匹配都要回溯很多次，是不是会使算法的时间复杂度退化到非线性呢？

其实不然，我们对代码中的几个变量进行讨论，首先是kmp函数，显然决定kmp函数时间复杂度的变量只有两个，i和j，其中i只增加了len次，是O(len)的，下面讨论j,因为由next数组的定义我们知道next[j]<j,所以在回溯的时候j至少减去了1，并且j保证是个非负数。另外，由代码可知j最多增加了len次，且每次只增加了1。简单来说，j每次增加只能增加1，每次减小至少减去1，并且保证j是个非负数，那么可知j减小的次数一定不能超过增加的次数。所以，回溯的次数不会超过len。综上所述，kmp函数的时间复杂度为O(len)。同理，对于计算next数组同样用类似的方法证明它的时间复杂度为O(len),这里不再赘述。对于长度为n的原始串S，和长度为m的模式串T，KMP算法的时间复杂度为O(n+m)。

参考文章：

1、字符串匹配的KMP算法：http://kb.cnblogs.com/page/176818/

2、KMP算法总结：http://blog.csdn.net/dyx404514/article/details/41314009

3、KMP算法解析：http://www.ituring.com.cn/article/59881

4、KMP算法学习与总结：http://www.cnblogs.com/goagent/archive/2013/05/16/3068442.html (含next数组求解优化)