假设检验中两种错误与样本容量的关系，样本容量，抽样分布的一些内容

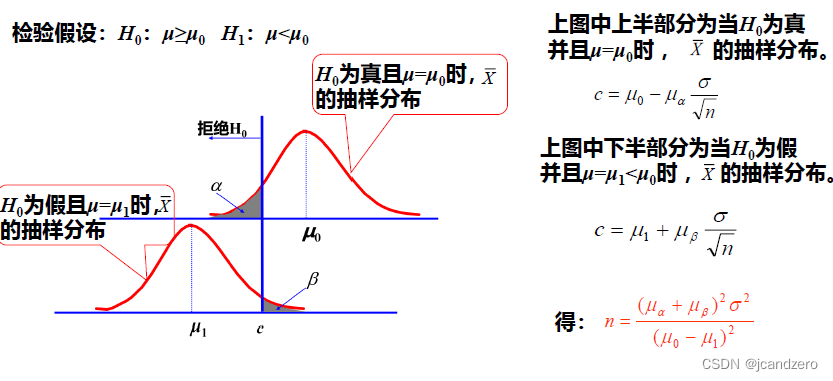
样本容量本身的计算公式。

这个标准正态分布的临界值

n=Z方（/2） 总体方差 /可接受的边际误差。

求出来就是最小能够接受的样本容量。

标准正态分布的边界值z可以查询标准 正态分布表得到

抽样分布部分知识点

回顾：统计抽样基本概念
 总体由研究对象的全体所组成。
 样本是总体中的部分元素所组成的集合。
 目标总体是我们要推断的总体
 抽样总体是实际抽取样本的总体
 在抽样之前，应将总体划分为抽样单位。抽样单位既可以是
一个简单的个体，也可以是一组个体。
对某一个特殊研究，抽样单位的名册称为抽样框。

一、简单随机抽样

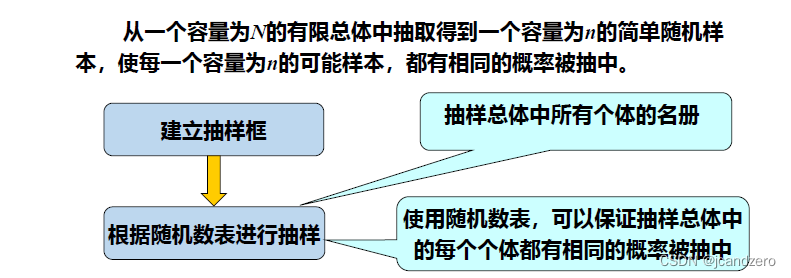
我们主要考虑这些

 1、总体均值

2、总体比率

3、样本容量的确定

如果选择大样本（n≥30），则中心极限定理可以保证的抽样分布
近似服从正态概率分布，μ 的区间估计为：

 其中

 

 

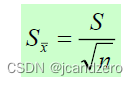
总体比率的区间估计

而在随机抽样当中

 

标准差要进行修正。 

这里有一点点不一样啊。

 二、分层随机抽样

 

 三、整群抽样

例如，我们想调查某省的登记选民。则有两种方法：

 整群抽样与分层抽样的比较：
分层抽样和整群抽样都将总体划分为组，因此这两种抽样过程感觉
上是相似的。
• 当群内的个体存在差异时，整群抽样可提供较好的结果。
选择整群抽样与分层抽样的原因是不同的。
• 理想情形是每一群是整个总体的一个缩影，这时，抽取很少的群就
可以提供关于整个总体特征的信息。

 四、系统抽样

例如，需要从容量为5000的总体中抽取一个容量为50的样本，我们
可以从总体中随机选择一个，然后在其后面的抽样框中，每隔100个个体
选择一个，可得到样本中其余的个体。
因为第一个个体的选择是随机的，因此系统样本常常假定具有简单随
机样本的性质。当抽样框是由总体中的个体随机排列而形成时，这种假定
通常是合适的。