图的邻接矩阵和DFS遍历

图的存储结构相对于线性表和树来说，是复杂了许多，而不是用一个线性表或者链表就能定义的。对于图来说，它的存储方式有邻接矩阵，邻接表，十字链表，邻接多重表和边集数组。在这里，要介绍的是如果使用邻接矩阵和邻接表来存储图结构。

一、邻接矩阵

图的邻接矩阵存储是用两个数组来完成的。一个一维数组存储定点信息（称为顶点数组），一个二维数组存储边信息（称为边数组）。
下面介绍不同类型的邻接矩阵的定义。

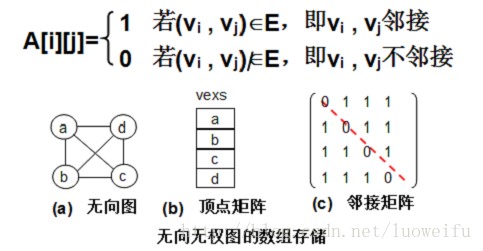
1. 无向图的邻接矩阵

（1） 无权图的邻接矩阵

无权图G=（V,E）的定义如下：

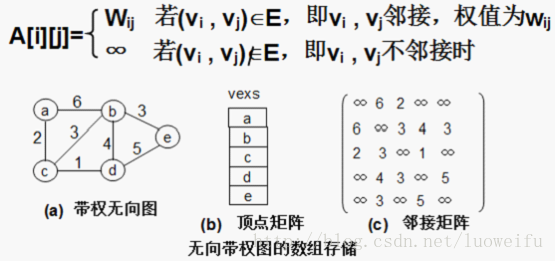
（2）有权图的邻接矩阵

无权图G=（V,E）的定义如下：

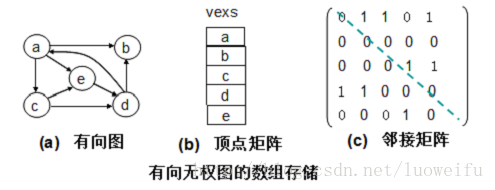
2. 有向图的邻接矩阵

（1） 无权图的邻接矩阵

无权图G=（V,E）的定义如下：

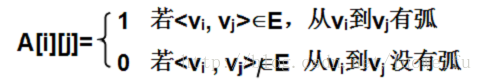
（2）有权图的邻接矩阵

无权图G=（V,E）的定义如下：

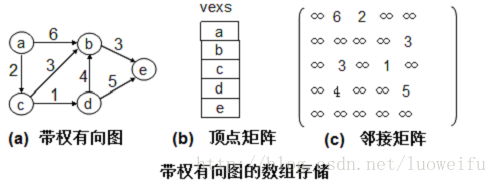
可以看到，对于无权图来说，0表示此边( i , j )或< i , j >不存在，1则反之；对于有权图来说，具体的数值表示此边( i , j )或< i , j >的权值，而无穷符号则表示此边不存在。

代码实现

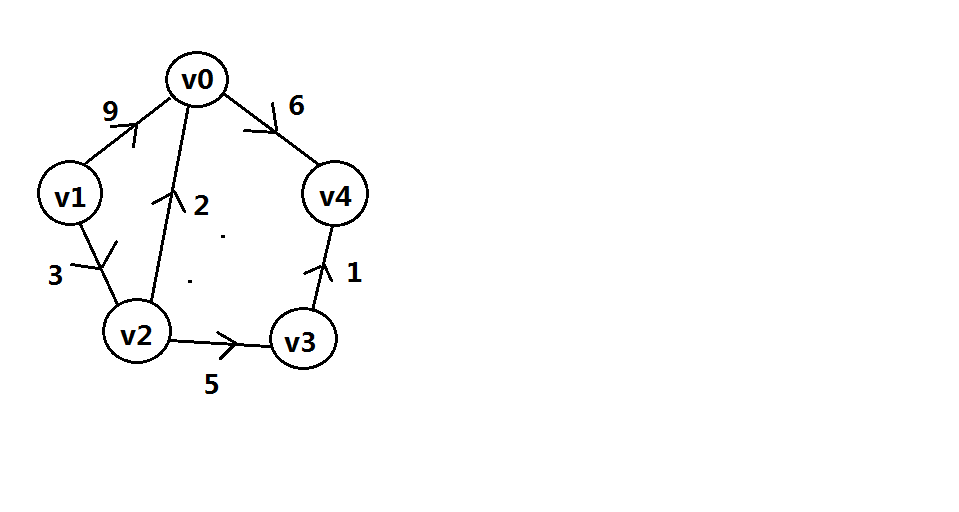
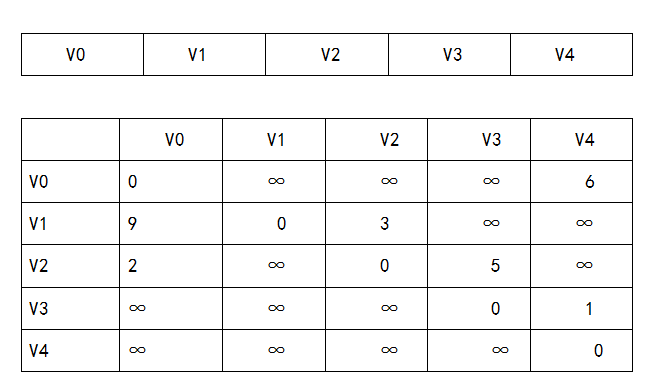
假如我们要对此图建立邻接矩阵

则建立的顶点数组和邻接矩阵如下：

#include <stdio.h>
#include <stdlib.h>
//const int MAXVEX = 100;
#define MAXVEX 100
#define INFINITT 65535  //表示无穷 
int visited[MAXVEX];

typedef struct{
    char vexs[MAXVEX];//顶点表 
    int arc[MAXVEX][MAXVEX];//边表
    int numV, numE;//顶点数和边数 
}MGraph;

void createGraph(MGraph *G){
    int i,j,k,w;
    printf("请输入顶点数和边数：");
    scanf("%d%d", &G->numV, &G->numE);
    //建立结点 
    for(i = 0; i < G->numV; i++){
        scanf("%d", &G->vexs[i]);
    }
    //初始化边为无穷 
    for(i = 0; i < G->numV; i++){
        for(j = 0; j < G->numV; j++){
            G->arc[i][j] = INFINITT;
        }
    }
    //建立边
    printf("输入边的左右两个坐标:\n");
    for(k = 0; k < G->numE; k++){
        scanf("%d%d%d", &i,&j,&w);
        G->arc[i][j] = w;
        G->arc[j][i] = G->arc[i][j];
    } 
}

int main(){
    MGraph G;
    createGraph(&G);
}

二、图的DFS遍历

图的DFS遍历，类似树的DFS遍历。从图中的某个顶点v开始，访问此节点，然后从v的未访问的邻接点开始再进行DFS遍历，直到所有和v想通的顶点都被访问到。

代码实现

void DFS(MGraph G, int i){
    int j;
    printf("%d ", G.vexs[i]);
    visited[i] = 1;
    for(j = 0; j < G.numV; j++){
        if(G.arc[i][j] != 0 && G.arc[i][j] != INFINITT && !visited[j]){
            DFS(G, j);
        }
    }
}

void DFSTraverse(MGraph G){
    int i;
    for(i = 0; i < G.numV; i++){
        visited[i] = 0;
    }
    for(i = 0; i < G.numV; i++){
        if(!visited[i]){
            DFS(G, i);
        }
    }
}

完整代码

include <stdlib.h>
//const int MAXVEX = 100;
#define MAXVEX 100
#define INFINITT 65535  //表示无穷 
int visited[MAXVEX];

typedef struct{
    char vexs[MAXVEX];//顶点表 
    int arc[MAXVEX][MAXVEX];//边表
    int numV, numE;//顶点数和边数 
}MGraph;

void createGraph(MGraph *G){
    int i,j,k,w;
    printf("请输入顶点数和边数：");
    scanf("%d%d", &G->numV, &G->numE);
    //建立结点 
    for(i = 0; i < G->numV; i++){
        scanf("%d", &G->vexs[i]);
    }
    //初始化边为无穷 
    for(i = 0; i < G->numV; i++){
        for(j = 0; j < G->numV; j++){
            G->arc[i][j] = INFINITT;
        }
    }
    //建立边
    printf("输入边的左右两个坐标:\n");
    for(k = 0; k < G->numE; k++){
        scanf("%d%d%d", &i,&j,&w);
        G->arc[i][j] = w;
        G->arc[j][i] = G->arc[i][j];
    } 
} 

void DFS(MGraph G, int i){
    int j;
    printf("%d ", G.vexs[i]);
    visited[i] = 1;
    for(j = 0; j < G.numV; j++){
        if(G.arc[i][j] != 0 && G.arc[i][j] != INFINITT && !visited[j]){
            DFS(G, j);
        }
    }
}

void DFSTraverse(MGraph G){
    int i;
    for(i = 0; i < G.numV; i++){
        visited[i] = 0;
    }
    for(i = 0; i < G.numV; i++){
        if(!visited[i]){
            DFS(G, i);
        }
    }
}

int main(){
    MGraph G;
    createGraph(&G);
    DFSTraverse(G);
}

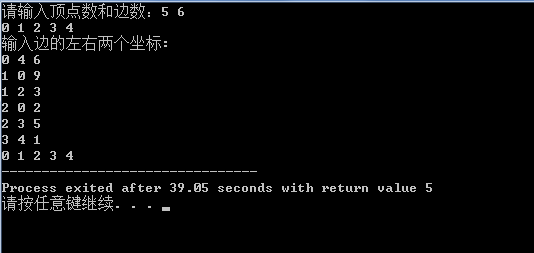
结果如下：