问题
面试常考的问题,给定一个数组,求前k小或者前k大。
解法:
1. 快速排序
2. 堆排序
3. 冒泡排序
解法(前k大和前k小思路相反,只说前k大情况)
1. 快速排序 近似O(n)
- 利用partition分割成两个数组left[] 和 right[]
- 如果此时分割点mid,小于k,说明left中都是前k大的,而且还要在right中取(k-mid)个数
- 如果mid大于k,说明前k大的数全部在left中,然后继续在left中找
ps:求前k小,则维持一个递增数列,求前k大,则维持一个递减数列
public class FastSortBeforeK {
static int[] array = new int[]{100,20,4,2,87,9,8,5,46,26};
public static void sort(int low, int high, int k){
if(low < high){
//先分出两个数组,mid为分割点
int mid = partition(low, high);
//左边的不够k个,还要在右边找
if(mid < k){
sort(mid+1, high, k-mid);
//前k个全部在左边
}else if(mid > k) {
sort(low, mid-1, k);
//刚好k个,直接输出
}else{
return;
}
}
}
public static int partition(int low, int high){
int privoteKey = array[low];
int back = privoteKey;
while(low < high){
//从右边数,大的全部放到左边
while(low<high && array[high] <= privoteKey){
high--;
}
//直到发现了有半部分有小于privotekey的数
array[low] = array[high];
//从左边数,小的全部放到右边
while(low<high && array[low] >= privoteKey){
low++;
}
array[high] = array[low];
}
array[low] = back;
return low;
}
public static void swap(int i, int j){
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
public static void main(String[] args){
int k = 6;
sort(0, array.length-1, k-1);
for(int i = 0; i < k; i++){
System.out.print(array[i] + " ");
}
}
}
2. 堆排序 O(nlogk)
求前k大,就维持一个k大小的小根堆,求前k小,就维持一个k大小的大根堆。
1. 由于我们是求前k大,所以我们构造一个小根堆
2. 从k+1开始,跟堆顶比较,由于小根堆的堆顶是根堆中最小的,如果节点都小于堆顶,自然不可能是前k大的,所以不能加进来
3. 如果大于堆顶,可以加进来
4. 每加一个进来,就要重新调节堆,使堆顶是前k个最小的
public class BeforeKHeap {
static int array[] = new int[]{0,50,10,90,30,70,40,80,60,20};
static int size = 9;
public void sort(int k){//k为4
//1. 首先构造根堆,为什么i为k/2,因为构造堆从底向上,定位到2
for(int i = k / 2; i >= 1; i--){
heapAdjust(i, k);
}
//构造完后,此时[10 30 90 50 70 40 80 60 20 ],见下图
for(int i = k+1; i <= size; i++){
//如果小于堆顶
if(array[i] > array[1]){
swap(1, i);
heapAdjust(1, k);
}
}
}
public void heapAdjust(int root, int end){
int temp = array[root];
for(int i = root * 2; i <= end; i*=2){
//这里不能<=,因为是为了维持k的根堆
if(i < end && array[i] > array[i+1]){
i++;
}
if(temp <= array[i]){
break;
}
array[root] = array[i];
root = i;
}
array[root] = temp;
}
public void swap(int i, int j){
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
public static void main(String args[]){
int k = 4;
new BeforeKHeap().sort(k);
for(int i = 1; i <= k; i++){
System.out.print(array[i] + " ");
}
}
}步骤:
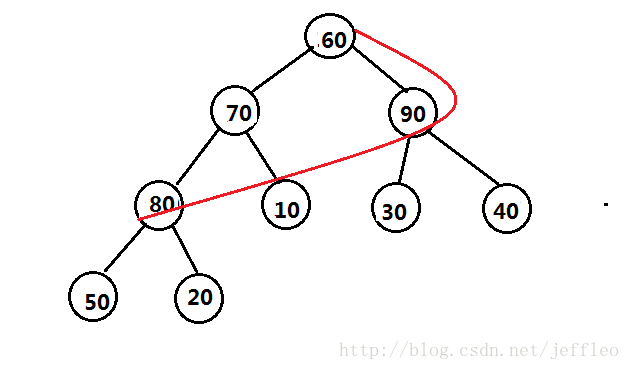
1、原堆

2、构造k=4的小根堆

3、开始从k+1的节点和堆顶比较

4、交换后重新调整

5、然后比较40,80,60,20,最终形成的根堆,前k个就是最大的k个
3. 冒泡排序 O(n*k)
只要冒到第k个就可以了,简单易理解
public class BeforeKMaopao {
public void sort(int[] array, int k){
//冒到k就跳出
for(int i = 0; i < k; i++){
for(int j = array.length - 1; j > i; j--){
if(array[j] > array[j-1]){
swap(array, j, j-1);
}
}
}
}
public void swap(int[] array, int i, int j){
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
public static void main(String[] args){
BeforeKMaopao sort = new BeforeKMaopao();
int[] array = new int[]{50,10,90,30,70,40,80,60,20};
sort.sort(array, 4);
for(int i = 0 ; i < 4; i++){
System.out.print(array[i] + " ");
}
}
}























 1297
1297

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








