二叉树中应用

最新推荐文章于 2024-11-04 15:37:16 发布

Zero-Talent

最新推荐文章于 2024-11-04 15:37:16 发布

阅读量36

点赞数

文章标签：数据结构开发语言 c语言学习算法 Powered by 金山文档

本文链接：https://blog.csdn.net/jhlmx/article/details/129097594

版权

文章介绍了二叉树的各种操作，包括四种遍历方法（前序、中序、后序和层序），计算二叉树的节点数量（遍历与分治两种方式），求解二叉树的高度，确定给定层数的节点数量，查找特定值的节点，以及判断是否为完全二叉树的方法。同时，文章还涵盖了二叉树的销毁功能。

摘要由CSDN通过智能技术生成

遍历

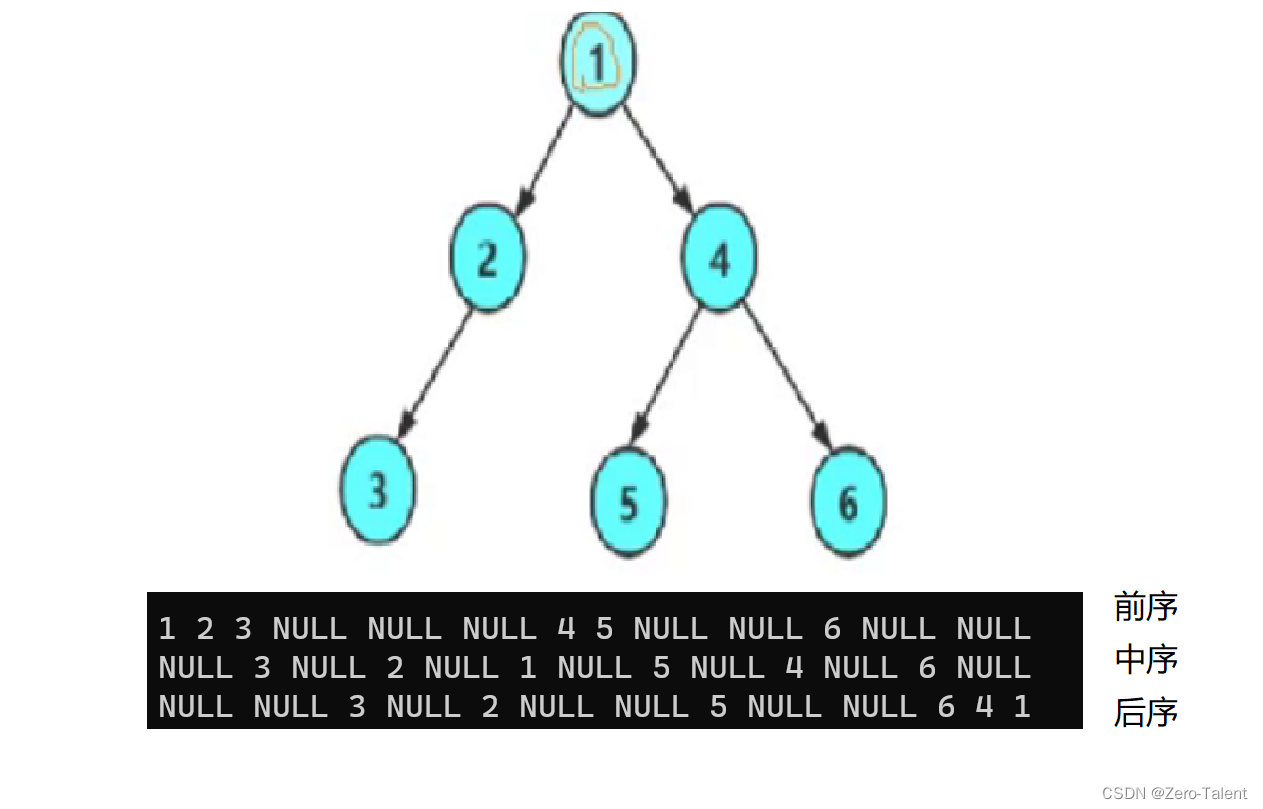
前序遍历：根左子树右子树

中序遍历：左子树根右子树

后序遍历：左子树右子树根

voidPreOrder(BTNode* root)//前序遍历{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	printf("%d ", root->a);
	PreOrder(root->left);
	PreOrder(root->right);
}

voidInOrder(BTNode* root)//中序遍历{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	InOrder(root->left);
	printf("%d ", root->a);
	InOrder(root->right);
}

voidPostOrder(BTNode* root)//后续遍历{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->a);
}

层序遍历

队列实现

先在队列中插入根节点

打印头节点，把头节点出队

如果子节点不为NULL就入队列

循环上述操作，直到队列为空

void LevelOrder(BTNode* root)
{
    Queue q;
    QueInit(&q);

    if (root)
        QuePush(&q, root);

    while (!QueEmpty(&q))
    {
        BTNode* front = QueFront(&q);

        if (front != NULL)
            printf("%d ", front->a);
        QuePop(&q);
        
        if(front->left!=NULL)
            QuePush(&q, front->left);
        if(front->right!=NULL)
            QuePush(&q, front->right);   
    }
    QueDestroy(&q);
}

二叉树大小

有两种方法，一种是遍历，还有一种是分治

这两种方法区别就是遍历需要手动传入指向节点个数的指针，分治是先递归计算左右子树的节点个数，然后相加并加上根节点

时间复杂度都为O（N）

这里比较推荐第二种

遍历

这里size用指针是因为形参改变不影响实参

//void TreeSize(BTNode* root, int* psize)
//{
//    if (root == NULL)
//    {
//        return NULL;
//    }
//
//    (*psize)++;
//    TreeSize(root->left,psize);
//    TreeSize(root->right,psize);
//}

分治

int TreeSize(BTNode* root)
{
    if (root == NULL)
    {
        return NULL;
    }
    
    return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

二叉树的高度

这里需要用lheight跟rheight来记录左右子树，如果不记录，三目运算符比较时还会再次递归

int TreeHeight(BTNode* root)
{
    if (root == NULL)
    {
        return NULL;
    }

    int lheight = TreeHeight(root->left);
    int rheight = TreeHeight(root->right);

    return lheight > rheight ? lheight + 1 : rheight + 1;
}

int TreeHeight(BTNode* root)//不推荐
{
    if (root == NULL)
    {
        return NULL;
    }

    return TreeHeight(root->left) > TreeHeight(root->right) ?
        TreeHeight(root->left) + 1 :
        TreeHeight(root->right) + 1;
}

二叉树任意层数节点个数

算k层有多少节点，只需要计算上一层节点有多少子节点

int TreeLevel(BTNode* root, int k)
{
    if (root == NULL)
    {
        return NULL;
    }

    if (k == 1)
    {
        return 1;
    }

    int lheight = TreeLevel(root->left,k-1);
    int rheight = TreeLevel(root->right,k-1);

    return  lheight + rheight;
}

二叉树查找为x的节点

BTNode* TreeFind(BTNode* root, BTData x)
{
    if (root == NULL)
    {
        return NULL;
    }

    if (root->a == x)
    {
        return root;
    }

    BTNode* lret = TreeFind(root->left, x);
    if (lret)
    {
        return lret;
    }

    BTNode* rret = TreeFind(root->right, x);
    if (rret)
    {
        return rret;
    }

    return NULL;
}

判断是否为完全二叉树

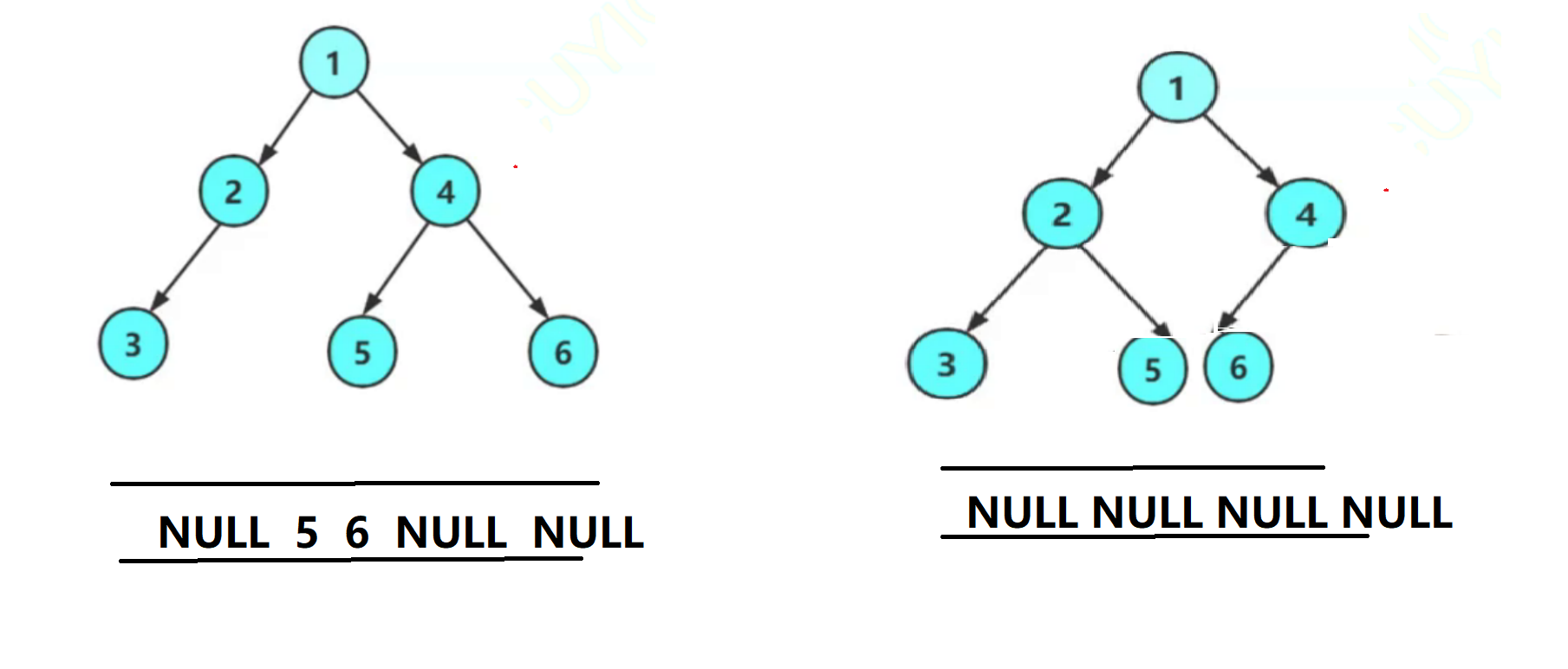
利用队列来实现，逻辑跟层序遍历类似

首先将父节点节点插入队列，然后队头出父节点节点，再插入子节点。

当队头为空指针时，会发现完全二叉树队列全空，而非完全二叉树中队列还有数

之后队头出数据，遇到不为空返回false

bool TreeComplete(BTNode* root)
{
    Queue q;
    QueInit(&q);

    if (root)
        QuePush(&q, root);

    while (!QueEmpty(&q))
    {
        BTNode* front = QueFront(&q);
        QuePop(&q);

        if (front == NULL)
            break;

        QuePush(&q, front->left);
        QuePush(&q, front->right);
    }

    while (!QueEmpty(&q))
    {
        BTNode* front = QueFront(&q);
        QuePop(&q);
        if (front != NULL)
        {
            return false;
        }
    }

    return true;
}

二叉树的销毁

这里销毁二叉树之后并没有把根节点置空，需要在外部置空root

形参改变不影响实参，如果想要在函数内部把root置空就需要传root的地址，用二级指针来接收

void TreeDestroy(BTNode* root)
{
    if (root == NULL)
    {
        return NULL;
    }

    TreeDestroy(root->left);
    TreeDestroy(root->right);
    free(root);
}