二叉树(Binary Tree):二叉树是一棵树,其中每个结点都不能有多于两个的子结点;
特点:
(1) 每个结点最多有两棵子树,没有子树或者只有一棵子树也是可以的;
(2)左子树和右子树是有顺序的,次序不能任意颠倒;
(3)即使树中只有一棵子树,也要区分它是左子树还是右子树;
特殊的二叉树:
(1)斜树:顾名思义,斜树一定是要斜的;所有的结点都只有左子树的二叉树叫左斜树,所有的结点都只有右子树的二叉树叫右斜树;其实,线性表就可以理解为树的一种特殊的表现形式;
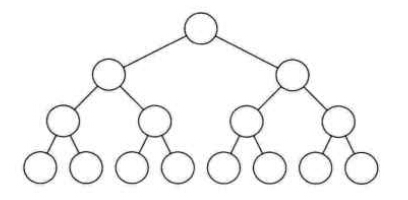
(2)满二叉树:在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树;如图:
(3)完全二叉树:对一棵具有n个结点的二叉树按层序编号,如果编号为i的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同,那么这棵二叉树称为完全二叉树;或者这样理解:在一棵二叉树中,除最后一层外,若其余层都是满的,并且最后一层或者是满的,或者是右边缺少连续若干个结点,则称此树为完全二叉树;
所以我们可以这样判断完全二叉树:那就是看着树的示意图,心中默默给每个结点按照满二叉树的结构逐层顺序编号,如果编号出现空档,就说明不是完全二叉树,否则就是;
二叉树的实现:同样,二叉树也可以通过顺序存储和链式存储来实现;
二叉树的顺序存储就是用一维数组存储二叉树中的结点,并且结点的存储位置,也就是数组的下标要能体现结点之间的逻辑关系,比如父结点与子结点的逻辑关系,子结点 与子结点之间的关系;但顺序存储的实用性不强;
所以一般采用链式存储;
二叉树的遍历:是指从根结点出发,按照某种次序,依次访问二叉树中所有结点,使得每个结点被访问一次且仅被访问一次;
二叉树的遍历方式有好多种,如果我们限制了从左到右的习惯方式,那么主要就有以下几种:
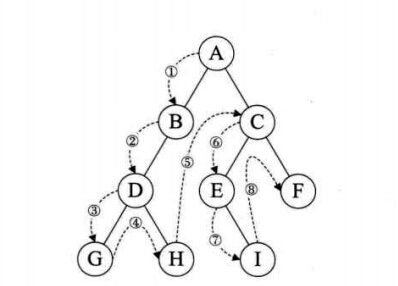
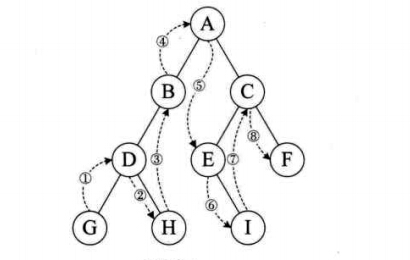
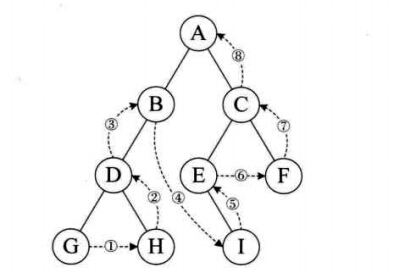
(1)前序遍历:先访问子结点,然后前序遍历左子树,再前序遍历右子树;如下图,遍历顺序是:ABDGHCEIF
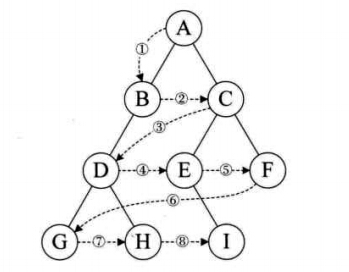
(2)中序遍历:从根结点开始(但并不是先访问根结点),中序遍历根结点的左子树,然后方式根结点,最后中序遍历右树,如图,遍历的顺序是:GDHBAEICF
(3)后序遍历:从左到右先叶子后结点的方式遍历访问左右子树,最后是访问根结点;如图,遍历的顺序是:GHDBIEFCA
(4)层序遍历:从树的第一层,也就是根结点开始访问,从上而下逐层遍历,在同一层中,按从左到右的顺序对结点进行逐个访问;如图,遍历顺序为:ABCDEFGHI
代码如下:
二叉树结点
package binaryTree;
// 二叉树节点
public class BTNode
{
private char key; // 数据
private BTNode left, right; // 左右子结点
public BTNode(char key)
{
this(key, null, null);
}
public BTNode(char key, BTNode left, BTNode right)
{
this.key = key;
this.left = left;
this.right = right;
}
public char getKey()
{
return key;
}
public void setKey(char key)
{
this.key = key;
}
public BTNode getLeft()
{
return left;
}
public void setLeft(BTNode left)
{
this.left = left;
}
public BTNode getRight()
{
return right;
}
public void setRight(BTNode right)
{
this.right = right;
}
}
二叉树遍历:
package binaryTree;
import java.util.Stack;
// 遍历二叉树
public class BinTree
{
protected BTNode root;
public BinTree(BTNode root)
{
this.root = root;
}
public BTNode getRoot()
{
return root;
}
// 初始化,构造二叉树
public static BTNode init()
{
BTNode a = new BTNode('A');
BTNode b = new BTNode('B', null, a);
BTNode c = new BTNode('C');
BTNode d = new BTNode('D', b, c);
BTNode e = new BTNode('E');
BTNode f = new BTNode('F', e, null);
BTNode g = new BTNode('G', null, f);
BTNode h = new BTNode('H', d, g);
return h; // 根结点
}
// 访问节点
public static void visit(BTNode p)
{
System.out.print(p.getKey() + " ");
}
// 递归实现前序遍历
protected static void preorder(BTNode p)
{
if (p != null)
{
visit(p);
preorder(p.getLeft());
preorder(p.getRight());
}
}
// 递归实现中序遍历
protected static void inorder(BTNode p)
{
if (p != null)
{
inorder(p.getLeft());
visit(p);
inorder(p.getRight());
}
}
// 递归实现后序遍历
protected static void postorder(BTNode p)
{
if (p != null)
{
postorder(p.getLeft());
postorder(p.getRight());
visit(p);
}
}
// 非递归实现前序遍历
protected static void iterativePreorder(BTNode p)
{
Stack<BTNode> stack = new Stack<BTNode>();
if (p != null)
{
stack.push(p);
while (!stack.empty())
{
p = stack.pop();
visit(p);
if (p.getRight() != null)
stack.push(p.getRight());
if (p.getLeft() != null)
stack.push(p.getLeft());
}
}
}
// 非递归实现后序遍历
protected static void iterativePostorder(BTNode p)
{
BTNode q = p;
Stack<BTNode> stack = new Stack<BTNode>();
while (p != null)
{
// 左子树入栈
for (; p.getLeft() != null; p = p.getLeft())
stack.push(p);
// 当前结点无右子结点或右子结点已经输出
while (p != null && (p.getRight() == null || p.getRight() == q))
{
visit(p);
q = p; // 记录上一个已输出结点
if (stack.empty())
return;
p = stack.pop();
}
// 处理右子结点
stack.push(p);
p = p.getRight();
}
}
// 非递归实现中序遍历
protected static void iterativeInorder(BTNode p)
{
Stack<BTNode> stack = new Stack<BTNode>();
while (p != null)
{
while (p != null)
{
if (p.getRight() != null)
stack.push(p.getRight()); // 当前结点右子结点入栈
stack.push(p); // 当前结点入栈
p = p.getLeft();
}
p = stack.pop();
while (!stack.empty() && p.getRight() == null)
{
visit(p);
p = stack.pop();
}
visit(p);
if (!stack.empty())
p = stack.pop();
else
p = null;
}
}
public static void main(String[] args)
{
BinTree tree = new BinTree(init());
System.out.print(" 递归实现前序遍历:");
preorder(tree.getRoot());
System.out.println("\n");
System.out.print(" 递归实现中序遍历:");
inorder(tree.getRoot());
System.out.println("\n");
System.out.print(" 递归实现后序遍历:");
postorder(tree.getRoot());
System.out.println("\n");
System.out.print(" 非递归实现前序遍历:");
iterativePreorder(tree.getRoot());
System.out.println("\n");
System.out.print(" 非递归实现中序遍历:");
iterativeInorder(tree.getRoot());
System.out.println("\n");
System.out.print(" 非递归实现后序遍历:");
iterativePostorder(tree.getRoot());
System.out.println("\n");
}
}






















 5106
5106

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








