OO第一单元总结

目录

前言

第一次作业

目标

架构设计

度量分析

自己的Bug

发现Bug的策略

第一次作业总结

第二次作业

目标

架构设计 

度量分析

Bug分析 

第二次作业总结

第三次作业

目标

架构设计

度量分析

第三次作业总结

心得体会

---

前言

OO的第一单元是完成单变量多项式的括号展开，主要是对表达式进行合并及扩展得到恒等的表达式。目标是在第一单元作业中体会层次化设计的思想的应用和工程实现。

第一次作业

目标

读入一个包含加、减、乘、乘方以及括号（其中括号的深度至多为 1 层）的单变量表达式，输出恒等变形展开所有括号后的表达式。

架构设计

第一次作业采用了递归下降法，利用Lexer词法解析器对输入进行处理，通关lexer.next()得到表达式中的字符串。Parser则是作为语法解析器对读入的字符进行处理，将表达式解析成表达式（Expr类 ）、项 （Term类）、因子 (Factor类）。Expr类、Term类、Variable类和Number类对读入的字符串进行分层管理，并用Factor接口集中，初步体现了层次化设计的思想。

本次作业中表达式展开的最终结果其实是一个多项式。而多项式中含有一系列的单项式，每个单项式都是（+|-）常数 x^指数 这种形式。于是可以建立两个类：Poly类和Mono类。

Mono类含有四个变量：op、index、variable、power来存储单项式。

Poly类有一个ArrayList容器，用来存储Mono，此外还有addPoly()，mulPoly()和powPoly()等方法来实现多项式的运算,最后用toString()方法将每个Mono的字符串形式链接起来，形成表达式字符串。之后在Expr、Term、Factor等类中都写一个goPoly()方法，将类中的内容转化为多项式。

度量分析

• 代码规模分析

• 类复杂度分析

• 方法的复杂度分析

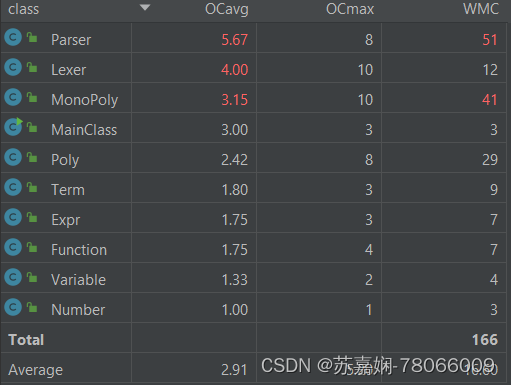
在我的架构中Parser类的复杂度最高，其次是Lexer类和Poly类。而在方法复杂度中，parsefactor()方法和simplify()方法的复杂度最高。

自己的Bug

在互测阶段本人被hack了两个bug。其中一个bug是没考虑到x^0的情况，这个bug很好解决就是在变量因子中加一个判断条件，若指数为0则返回1。第二个bug是表达式因子的符号判断问题。这个bug也是通过判断条件检查因子是否为表达式因子再对符号进行处理。

发现Bug的策略

根据指导书给的形式化表述及根据各个情况构造测试集，尽可能对作业进行全面的测试。

第一次作业总结

通过课程组给的训练及实验，本人顺利完成了第一次作业的要求。由于第一次作业通过Arraylist<>来存储变量，并没有考虑到自变量有多个如x*y的情况，造成了之后一个项拥有多个不同自变量的表达式合并的问题。

第二次作业

目标

在第一次作业基础上，本次迭代作业增加了以下几点：

• 支持嵌套多层括号。
• 新增指数函数因子，指数函数括号内部包含任意因子。
• 新增自定义函数因子，但自定义函数的函数表达式中不会调用其他自定义函数。

架构设计 

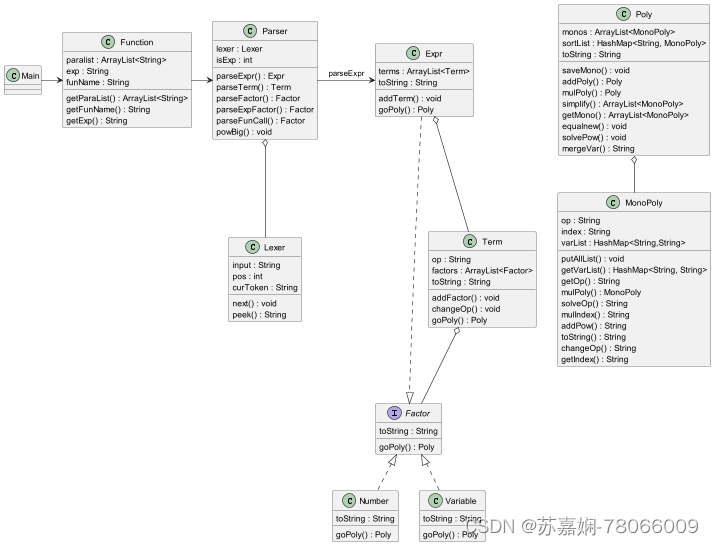
本次作业在第一次作业的基础上增加了Function类 。Function类的作用是解析及存储定义的函数。在Function类中，成员paralist用于存储形参、exp用于存储函数表达式、funName用于存储函数名字。在Main类中，会有funlist用于存储多个函数定义并传递进parser类中。

在Parser类中新增了两个方法：parseExpFactor() 和 parseFunCall()。

parseExpFactor方法用于解析指数函数，对于指数括号内的表达式进行解析及化简，当解析后得到的返回结果是Expr类时将增加括号以符合形式表述。

parseFunCall方法用于解析函数调用。当检测到函数调用时，存储实参再取出funlist里同名的函数表达式然后进行字符串替换并得到新的表达式，将得到的表达式进行解析就完成了函数调用解析。

度量分析

• 代码规模分析 

• 类复杂度分析 

  

Bug分析 

在互测阶段没被测出bug，但是strong2 出现了问题。主要原因是该点是没有考虑到在多层括号嵌套背景下指数和系数均有可能超过int范围的问题，用int存储而不是用BigInteger存储，因此没有通过边界测试+压力测试。

第二次作业总结

由于不够细心没有对程序进行界测试导致strong2测试点不通过，由此可以在下一次作业构造更完善的测试集对代码进行边界测试。

 

第三次作业

目标

本次作业在第二次的作业基础上新增求导功能,新增求导算子 。求导因子可以出现在很多位置，包括函数调用实参，指数函数内部等。本次作业函数表达式中需支持调用已定义的函数。

架构设计

本次作业在第二次作业的基础上在Parser类中parseDelivation() 方法。当得到字符串为dx时对括号内的表达式解析之后进行求导。在parseDelivation() 方法中，对dx()里的表达式进行解析及合并展开得到Poly对象。再调用Poly类里的derivation()方法进行求导。

在MonoPoly类中新增了两个方法：monosDerivation() 和 monoDerivation()。

monosDerivation方法用于完成乘法法则的求导运算。

monoDerivation方法用于完成链式法则的求导运算和变量因子的求导运算。

度量分析

• 代码规模分析 

• 类复杂度分析 

• 方法复杂度分析  

第三次作业总结

由于求导是在Poly类和Mono类中进行求导，导致需要将表达式解析后进行求导的到新的表达式再构造新的对象对得到的表达式进行解析，这样求导因子才会返回求导过后factor对象。这导致了程序性能迟缓的现象也影响了性能分，之后应该进行优化以改善性能。

心得体会

经过了第一单元的三次作业，理解和掌握了层次化的设计，建立了抽象层次并对多层的对象归一化管理。对Java的语法及容器的使用更加熟悉，使得更容易完成作业。在测试部分过于依赖于同学的测评机、己构造数据时没有构造完善的测试集。在这三次的作业中，我觉得的难点是对程序的优化。由于实现的方法效率较低导致性能低，因此在性能上还需要改进。希望下一个单元也能顺利完成作业并取得进步。