DFA确定性有限状态机过滤敏感词

最新推荐文章于 2022-11-08 17:58:34 发布

风云来

最新推荐文章于 2022-11-08 17:58:34 发布

阅读量3.4k

点赞数

分类专栏：算法

本文链接：https://blog.csdn.net/chenjiayi_yun/article/details/51699923

版权

本文介绍了DFA确定性有限状态机的工作原理及其在网络过滤敏感词中的应用。在文字过滤系统中，DFA算法能有效减少计算，提高效率。通过多叉树结构实现的状态机，对输入的句子进行字符级扫描，避免重复查找，测试显示过滤一个关键字耗时约1.3微秒，性能表现优异。

摘要由CSDN通过智能技术生成

介绍

通常把确定的有穷状态自动机(有穷状态自动机也就是本文讨论的这种状态机)称为DFA，把非确定的有穷状态自动机称为NFA。

原理

状态机就是通过当前状态state和事件event得到下一个状态state，即state+event=nextstate

DFA确定性有限状态机是有限类型的事件和状态切换。

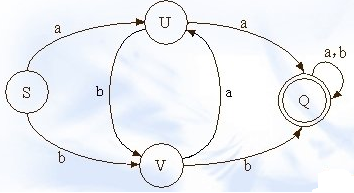
举个例子，存在4个状态，事件2个。

状态切换图吐下：

事件

a b

状态切换
S        U       V
U        Q       V
V        U       Q
Q        Q       Q

应用

网络过滤敏感词的常用算法。

在编译程序时，词法分析阶段将源代码中的语法符号变成语法的集合就是通过确定有限自动机实现的。

过滤敏感词

在文字过滤系统中，为了能够应付较高的并发，需要尽量减少计算。采用DFA算法基本没有什么计算，基本是状态转移。

本例中采用多叉树实现的有限状态机。每个utf8编码的中文字一般是3个字符，英文字母是一个字符。关键词表则是有限状态机的所有的状态。输入的句子被分成一个个字符，每个字符是一个ascii码，范围在0~255之间，以其为索引查找子树中的成员。每个子树包含256个数组成员，即最多是256个子节点，没有子节点的则为空。

这里的实现查找关键字不再重复查找已查找出来的关键字的的部分内容作为起点的词。

代码如下:

//dfa的多叉树
#define DFA_TREE_NODE_LEN (256)
/**
 * 树节点
 * 每个节点包含一个长度为256的数组
 */
struct TreeNode
{
    bool end;//关键词的终结
    std::vector<TreeNode*> subNodes;
    TreeNode()
    {
        end = false;
    }
    ~TreeNode()
    {
        for(oss::uint16 i &