图论算法：树上倍增法解决LCA问题（例题+cpp）

树上倍增法： LCA问题

树上倍增法用于求解LCA问题是一种非常有效的方法。

倍增是什么？ 简单来说，倍增就是 1 2 4 8 16 … 2^k

可以发现倍增是呈 2的指数型递增的一类数据，和二分一样，二分是缩小范围的，而倍增是扩大的，因此倍增与二分都具有 logn的时间复杂度，对于求解某些问题是非常高效的。

---

什么是树的公共祖先？

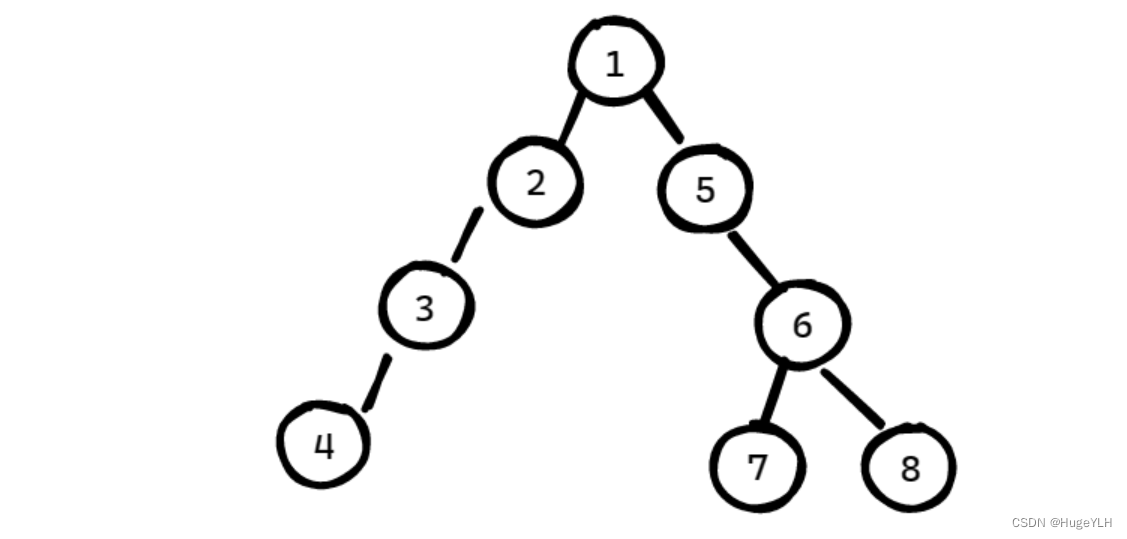
如图所示：

1. 节点 7与 节点8的最近公共祖先是 节点6
2. 节点3 与 节点5的最近公共祖先是 节点1

类似这种问题我们可以使用 树上倍增法来实现

---

树上倍增的实现：

首先定义 fa[i] [j] 表示 节点编号为 i 的节点，向根节点方向走了 2^j 步所到达的节点

• 什么是走了 2^j 步？？

对于节点7来说：

走一条边规定为走了一步，j可以表示为 0 ，1，2 ，分别代表走了 1步，2步，4步

走了一步： 到达了节点6

走了两步： 到达了节点5

走了四步：超过了范围，因此只能到达 节点1

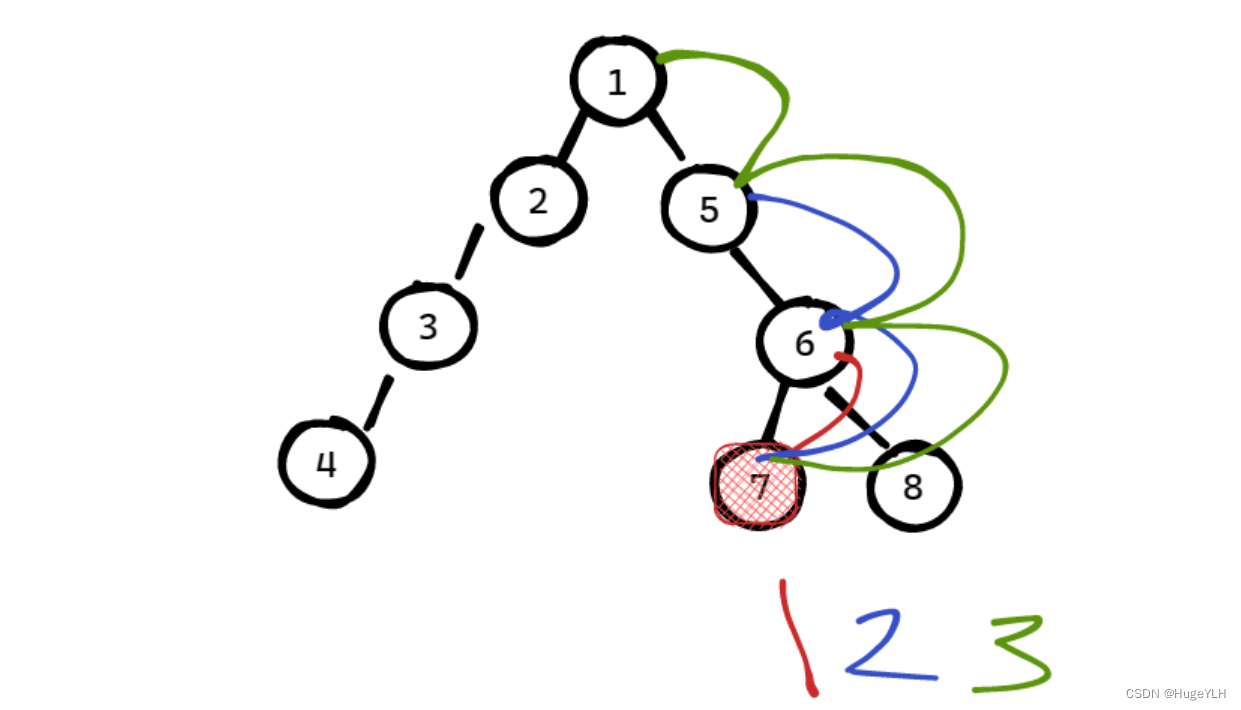
因此我们的 fa数组实际上记录的就是 节点 i 的 第 2^j 个祖先，分别为

• 1级祖先（直接祖先）：节点6；
• 2级祖先：节点5，
• 4级祖先（超过了，则就是根节点）：节点1
  （我自己取的名）

---

常数优化

首先我们创建一个lg数组：并且在输入完成每个节点的连接之后，执行如下的操作：

for (int i = 1; i <= n; i++)
{
     lg[i] = lg[i - 1] + (1 << lg[i - 1] == i);
 }

执行效果如下：

1. i=1：lg[1]=1
2. i=2：lg[2]=2
3. i=3：lg[3]=2
4. i=4：lg[4]=3
5. i=5：lg[5]=3
   …
6. i=8：lg[8]=4

这就是一个常数优化的过程

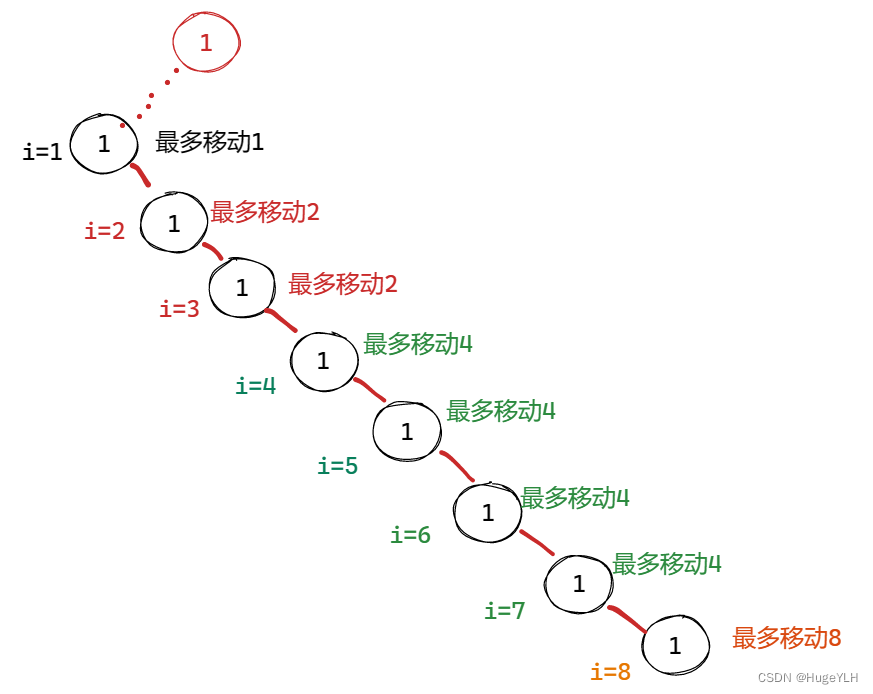
如图所示：由于我们前面已经说了，每个节点最多可以 移动 2^i 步
因此做这个lg数组其实就是为了方便以后的移动过程。
可以看出这也是他们的深度

因此节点的深度决定了他们的最大移动步数

---

预处理过程

首先把整个树结构存储起来（使用链式前向星）

然后首先对整个图进行预处理

• 预处理的目标：

就是把每个节点的 第 2^j 个的祖先找出来，用于之后的处理，同时我们还需要记录每个节点的深度，我们采用递归的形式，每次递归，节点的深度都是父节点的深度+1

注意：lg数组预处理每个节点的当前深度+1，可以使得某些地方得到优化

void init(int now,int father)
{
    fa[now][0]=father;//直接祖先：第now节点的第2^0个父亲节点，即第一个父亲节点是father
    depth[now]=depth[father]+1;//now的深度是父亲节点深度+1
    for (int i=1;i<=lg[depth[now]];i++)
    {
        fa[now][i]=fa[fa[now][i-1]][i-1];//初始化fa数组
    }
    //递归预处理当前点的所有子节点
    for (int i=head[now];i;i=edge[i].next)
    {
        if (edge[i].to!=father)  //不等于父亲的时候进入递归
        {
            init(edge[i].to,now); //孩子成为当前点，当前点成为父亲
        }
    }
}

这段代码是什么意思？

for (int i=1;i<=lg[depth[now]];i++)
{
     fa[now][i]=fa[fa[now][i-1]][i-1];//初始化fa数组
 }

由于我们之前已经处理过 lg数组了，lg数组就是某个节点的在某个深度能够进行的最大移动步数

因此根据节点的深度处理出他们不同步数能够到达的不同位置节点。

i=1：走 2^0 步的时候能够到达的节点？
i=2：走 2^1 的时候能够到达的节点？
i=3：走 2^2 的时候能够到达的节点？
i=4：走 2^3 的时候能够到达的节点？
一直到最大步数：lg[depth[i]]为止

举个例子：看上面的树图片

7节点的 fa可以表示为： lg[depth[7]]=3，因此最多移动3次（算上移动到根节点的父节点）
i=1：走 2^0 步：fa[7] [0]=6
i=2：走 2^1 步；fa[7] [1]=5
i=3：走 2^2 步，fa[7] [2]=0

7节点移动一步：到达节点6
7节点移动两步：到达节点5
7节点移动四步：到达根节点的父节点

---

寻找LCA的过程

我们会发现几个问题：

1. 两个节点的深度不一样，该如何寻找呢？
2. 什么时候寻找结束呢？ 即什么时候才能找到他们的LCA 呢

首先来看第一个问题：

深度不同怎么解决？ x和y节点

• 我们可以假设 x 节点的深度是最大的，即x节点是最靠近叶子节点的。
• 每次让x节点往根节点方向移动，直到x节点与y节点到达同一深度

什么时候结束寻找？ 即找到了最近公共祖先？

• 当他们位于同一深度的时候，让他们两个节点一起出发。
• 一起往上移动，直到不能再往上移动了为止，他们到达了一个相同的位置，这个位置的节点就是最近公共祖先的节点。

int LCA(int x,int y)
{
    if (depth[x]<depth[y]) swap(x,y);//假设x的深度大于等于y的深度
    while (depth[x]>depth[y])//让x与y到达同一深度，倍增x的深度
    {
        x=fa[x][lg[depth[x]-depth[y]]-1];
    }
    if (x==y) return x;//当他们相同时，LCA就是他们
    for (int k=lg[depth[x]]-1;k>=0;k--)//枚举每次移动的步数，x与y同时往根节点移动倍增，直到xy到达同一位置
    {
        if (fa[x][k]!=fa[y][k])
        {
            x=fa[x][k];
            y=fa[y][k];
        }
    }
    return fa[x][0];//xy到达同一位置，返回父节点
}

根据两个点的深度之差，计算出一次移动的最大移动步数，然后移动到上一个节点。

while (depth[x]>depth[y])//让x与y到达同一深度，倍增x的深度
{
    x=fa[x][lg[depth[x]-depth[y]]-1];
}

---

例如：我有以下的数据：

7 7 4
3 1
2 4
5 1
1 4
3 6
6 7

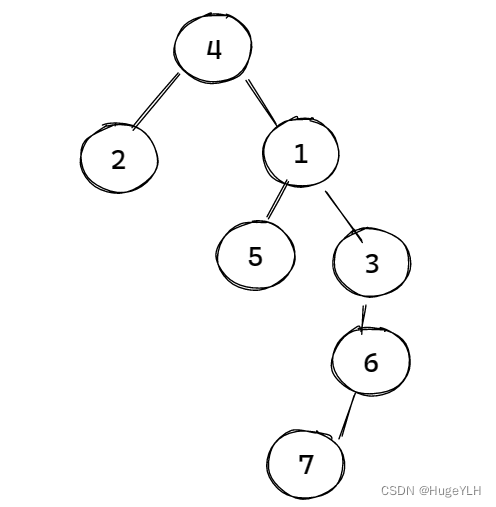
第一行分别表示 7个节点，7-1条边，4为根节点。
当我们输入完成后，首先进行初始化init：

递归完成后各项数据如下所示：

1. 4节点：深度为1，fa数组为0
2. 2节点：深度为2，fa数组为4
3. 1节点：深度为2，fa数组为4
4. 5节点：深度为3，fa数组为1，4
5. 3节点：深度为3，fa数组为1，4
6. 6节点：深度为4，fa数组为3，1
7. 7节点：深度为5，fa数组为6，3，4

然后测试两个点：

2，7点的LCA：x节点为2，y节点为7，x深度小于y，则x节点为7，y节点为2；然后x节点往根节点移动：

1. 通过lg数组可得x节点此时最多移动 2^1 步，则x节点到达3。
2. 此时x节点最多可以移动 2^0 步，则x节点到达1
3. 此时x节点为1与y的2节点处于同一层，因此两者同时移动，直到到达根节点。

同一层的移动情况是相同的

如果规定 分别求 7 到 其他节点的LCA，则他们在寻找LCA的过程中，在到达同一层的时候深度节点的移动情况如下所示：

1. 7节点和6节点： 到达fa[7] [0]=6节点
2. 7节点和3节点/5节点：到达fa[7] [1] =3节点
3. 7节点和1节点/2节点：首先到达fa[7] [1]=3节点，然后到达fa[3] [0]=1节点
4. 7节点和4节点：到达fa[7] [2]=4节点

---

模板例题：
最近公共祖先

完整AC code

//TODO: Write code here
int n,m,s;
const int N=1e6+10;
int nums[N];
struct Edge
{
    int to,w,next;
}edge[N];
int head[N],cnt;
int fa[N][50],depth[N],lg[N];
void add_edge(int u,int v)
{
    edge[++cnt].next=head[u];
    edge[cnt].to=v;
    head[u]=cnt;
}
void init(int now,int father)
{
    fa[now][0]=father;//第now节点的第2^0个父亲节点，即第一个父亲节点是father
    depth[now]=depth[father]+1;//now的深度是父亲节点深度+1
    for (int i=1;i<=lg[depth[now]];i++)
    {
        fa[now][i]=fa[fa[now][i-1]][i-1];//初始化fa数组
    }
    //递归预处理当前点的所有子节点
    for (int i=head[now];i;i=edge[i].next)
    {
        if (edge[i].to!=father)
        {
            init(edge[i].to,now);
        }
    }
}
int LCA(int x,int y)
{
    if (depth[x]<depth[y]) swap(x,y);//假设x的深度大于等于y的深度
    while (depth[x]>depth[y])//让x与y到达同一深度，倍增x的深度
    {
        x=fa[x][lg[depth[x]-depth[y]]-1];
    }
    if (x==y) return x;//当他们相同时，LCA就是他们
    for (int k=lg[depth[x]]-1;k>=0;k--)//枚举每次移动的步数，x与y同时倍增，直到xy到达同一位置
    {
        if (fa[x][k]!=fa[y][k])
        {
            x=fa[x][k];
            y=fa[y][k];
        }
    }
    return fa[x][0];//xy到达同一位置，返回父节点
}
signed main()
{
	cin>>n>>m>>s;
    for (int i=1;i<=n-1;i++)
    {
        int u,v;
        scanf("%lld%lld",&u,&v);
        add_edge(u,v);
        add_edge(v,u);
    }
    for (int i=1;i<=n;i++)
    {
        lg[i]=lg[i-1]+(1<<lg[i-1]==i);
    }
    init(s,0);
    for (int i=1;i<=m;i++)
    {
        int u,v;
        scanf("%lld%lld",&u,&v);
        printf("%lld\n",LCA(u,v));
    }
#define one 1
	return 0;
}

参考：树上倍增法