5.3 MATLAB学习笔记之绘图-三维图形

三维图形

三维图形具有更强的数据表现能力，为此MATLAB提供了丰富的函数来绘制三维图形。绘制三维图形与绘制二维图形的方法十分类似，很多都是在二维绘图的基础上扩展而来。

一、绘制三维曲线的基本函数

基本的三维图形函数为 plot3, 它是将二维绘图函数plot 的有关功能扩展到三维空间，用来绘制三维曲线。plot3 函数与plot函数用法十分相似，其调用格式如下：

plot3(x1,y1,z1, 选项1,x2,y2,z2,选项2,…,xn,yn,zn, 选项n)

• 其中，每一组x 、y 、z组成一组曲线的坐标参数，选项的定义和plot函数相同。
• 当x 、y 、z是 同长度的向量时，则x、y、z对应元素构成一条三维曲线。
• 当x、y、z是同型矩阵时，则以x、 y、z对应列元素绘制三维曲线，曲线条数等于矩阵列数。

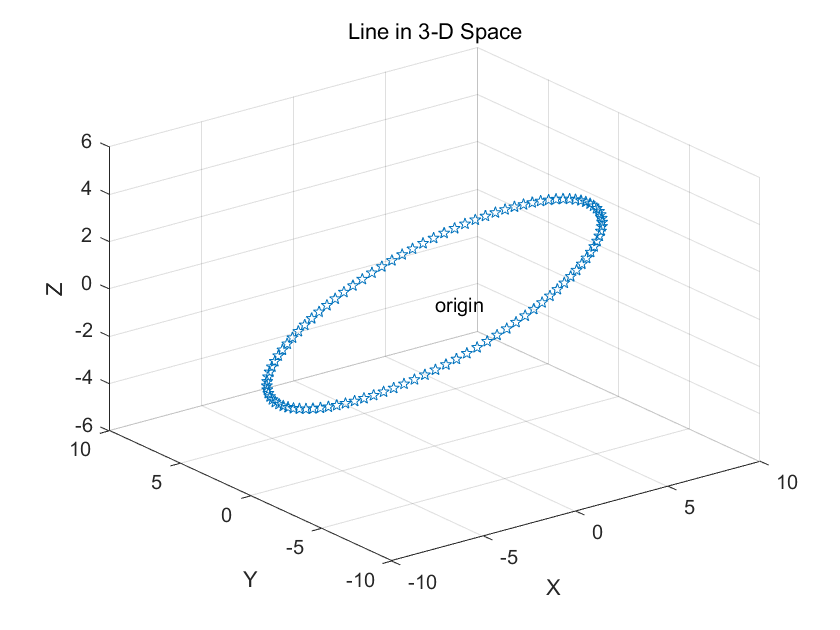
例1 绘制空间曲线：
$$\begin{gathered} x^2+y^2+z^2=64 \\ y+z=0 \end{gathered}$$
曲线所对应的参数方程为
$$\begin{gathered} x=8cost \\ y=4\sqrt{2}sint \\ z=-4\sqrt{2}sint \\ (0\le t\le 2\pi ) \end{gathered}$$

t=0:pi/50:2*pi;
x=8*cos(t);
y=4*sqrt(2)*sin(t);
z=-4*sqrt(2)*sin(t);
plot3(x,y,z,'p')
title('Line in 3-D Space')
text(0,0,0,'origin')
xlabel('X'),ylabel('Y'),zlabel('Z');grid

二、三维曲面

1.平面网格坐标矩阵的生成

绘制z=f(x,y)所代表的三维曲面图，先要在xy平面选定一矩形区域，假定矩形区域D=[a,b]×[c,d],

• 将[a,b] 在 x 方向分成m份，将[c,d]在y方向分成n份，由各划分点分别作平行于两坐标轴的直线，将区域D分成m×n个小矩形，
• 生成代表每一个小矩形顶点坐标的平面网格坐标矩阵，最后利用有关函数绘图。

产生平面区域内的网格坐标矩阵有以下两种方法。

(1)利用矩阵运算生成。

x=a:dx:b;
y=(c:dy:d)';
X=ones(size(y))*x;
Y=y*ones(size(x));

在上述程序段中，

• 矩阵X 的每一行都是向量x, 行数等于向量y 的元素的个数，
• 矩阵Y 的 每一列都是向量y, 列数等于向量x 的元素的个数。
• 于是X 和 Y 相同位置上的元素(X(i,j),Y(i,j) 恰好是区域D 的 (i,j) 网格点的坐标。
• 若根据每一个网格点上的x 、y 坐标求函数值z, 则得到函数值矩阵Z 。
• 显 然 ，X 、Y 、Z 各列或各行所对应坐标，对应于一条空间曲线，空间曲线的集合组成空间曲面。

(2) 利用meshgrid 函数生成。

x=a:dx:b;
y=c:dy:d;
[X,Y]=meshgrid(x,y);

程序段运行后，所得到的网格坐标矩阵X 、Y 与方法(1)得到的相同。

当x=y 时 ，meshgrid 函数可写成meshgrid(x)。

为了说明网格坐标矩阵的用法，下面举一个例子，该例子巧妙地利用网格坐标矩阵来解不定方程。

例2 已 知 6<x<30,15<y<36, 求不 定 方 程 2x+5y=126的整数解。

程序如下：

x=7:29;
y=16:35;
[x,y]=meshgrid(x,y);  		%在[7,29]×[16,35]区域生成网格坐标
z=2*x+5*y;
k=find(z==126);        		%找出解的位置   
x(k)',y(k)'             	%输出对应位置的x,y即方程的解

程序运行结果如下：

ans =

     8    13    18    23


ans =

    22    20    18    16

即方程共有4组解：(8,22)、(13,20)、(18,18)、(23,16)。

2.绘制三维曲面的函数

MATLAB提供了mesh 函数和surf 函数来绘制三维曲面图。

• mesh函数用于绘制三维网格图。 在不需要绘制特别精细的三维曲面图时，可以通过三维网格图来表示三维曲面。
• surf 用于绘制三维曲面图，各线条之间的补面用颜色填充。

mesh 函数和 surf 函数的调用格式如下：

mesh(x,y,z,c)

surf(x,y,z,c)

一般情况下，x 、y 、z 是同型矩阵。

• x 、y 是网格坐标矩阵，z 是网格点上的高度矩阵，c 称为色标 (color scale)矩阵，用于指定曲面的颜色。
• 在默认情况下，系统根据c 中元素大小的比例关系，把色标数据变换成色图矩阵中对应的颜色。
• c省略时 ，MATLAB 认为c=z, 亦即颜色的设定正比于图形的高度，这样就可以得出层次分明的三维图形。
• 当x、y 省略时，把z 矩阵的列下标当作x 轴坐标，把z矩阵的行下标当作y 轴坐标，然后绘制三维曲面图。
• 当x 、y是向量时，要求x 的长度等于z 矩阵的列数，y 的长度等于z 矩阵的行数，x 、y向量元素的组合构成网格点的x 、y坐标，z 坐标则取自z 矩阵，然后绘制三维曲面图。

例3 绘制三维曲面图z=sinycosx。

为便于分析各种三维曲面的特征，下面画出了3种不同形式的曲面。

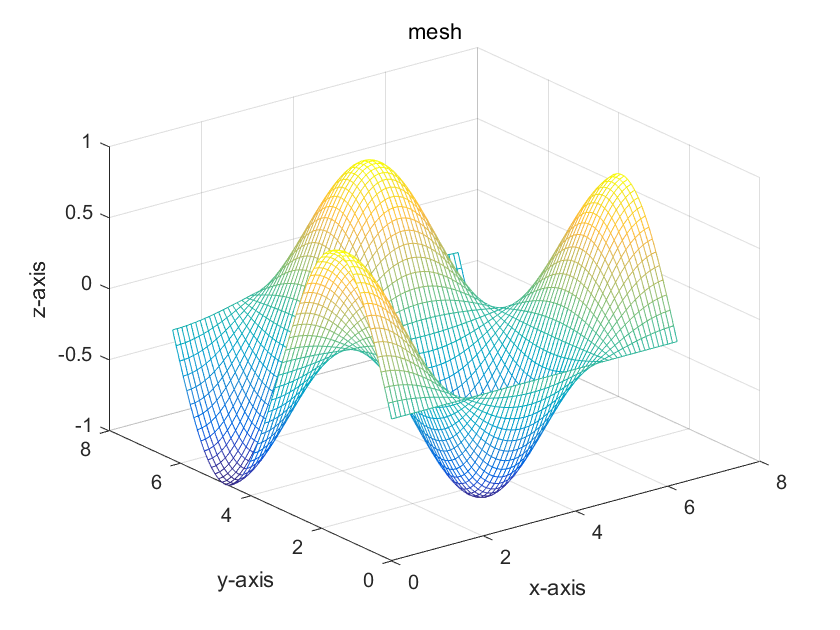
程序1:

x=0:0.1:2*pi;
[x,y]=meshgrid(x);
z=sin(y).*cos(x);
mesh(x,y,z)
xlabel('x-axis'),ylabel('y-axis'),zlabel('z-axis')
title('mesh')

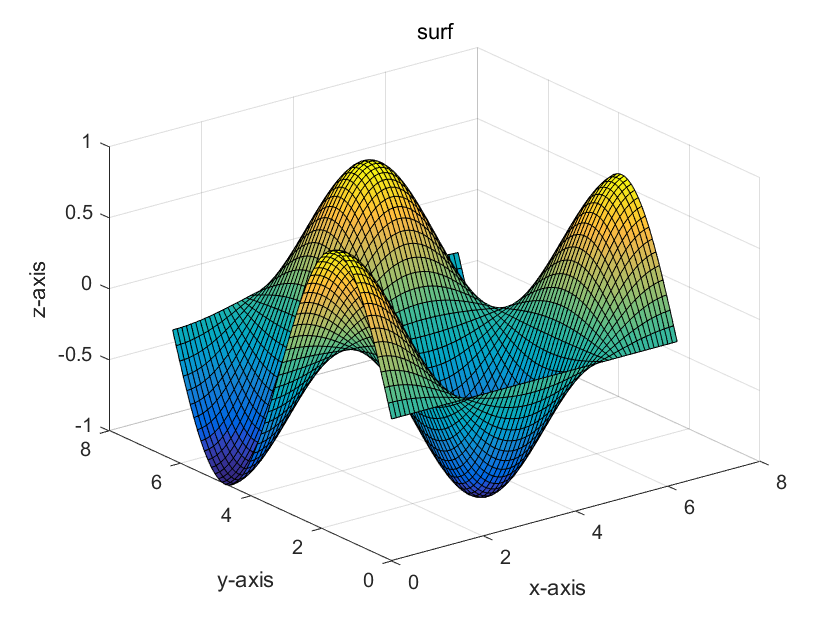
程序2:

x=0:0.1:2*pi;
[x,y]=meshgrid(x);
z=sin(y).*cos(x);
surf(x,y,z)
xlabel('x-axis'),ylabel('y-axis'),zlabel('z-axis')
title('surf')

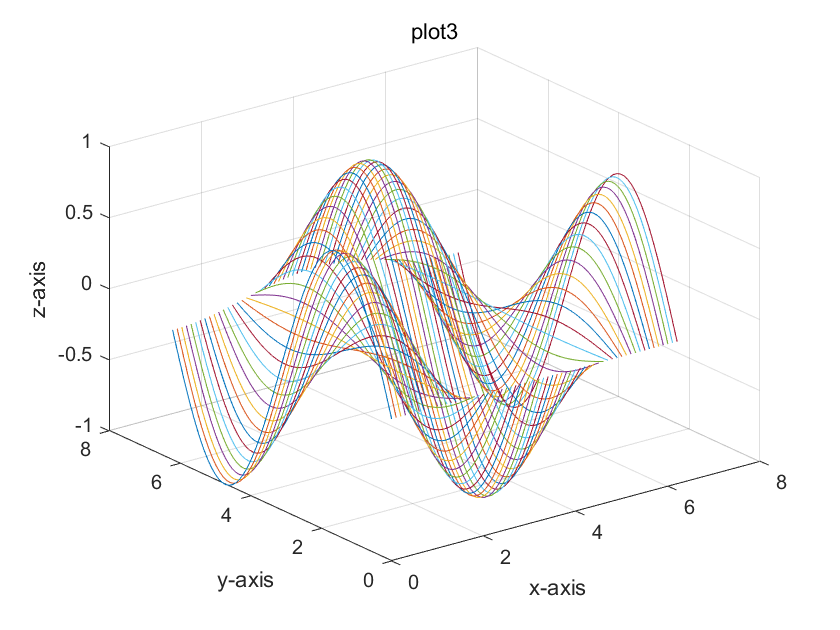
程序3:

x=0:0.1:2*pi;
[x,y]=meshgrid(x);
z=sin(y).*cos(x);
plot3(x,y,z)
xlabel('x-axis'),ylabel('y-axis'),zlabel('z-axis')
title('plot3');grid

• 网格图(mesh) 中线条有颜色，线条间补面无颜色。
• 曲面图(surf) 的线条是黑色，线条间补面有颜色。
• 曲面图补面颜色和网格图线条颜色都是沿z 轴变化的。
• 用plot3绘制的三维曲面实际上由三维曲线组合而成。

例4 绘制两个相互垂直且直径相等的圆柱体的相交图形。

程序如下：

m=30;
z=1.2*(0:m)/m;
r=ones(size(z));
theta=(0:m)/m*2*pi;
x1=r'*cos(theta);                  %生成第一个圆柱体的坐标矩阵
y1=r'*sin(theta);    
z1=z'*ones(1,m+1);
x=(-m:2:m)/m;
x2=x'*ones(1,m+1);                %生成第二个圆柱体的坐标矩阵
y2=r'*cos(theta); 
z2=r'*sin(theta);
surf(x1,y1,z1)                  %绘制垂直的圆柱体
axis equal,axis off
hold on
surf(x2,y2,z2)                 %绘制水平的圆柱体
axis equal,axis off
title('两个圆柱体的相交图形')
hold off

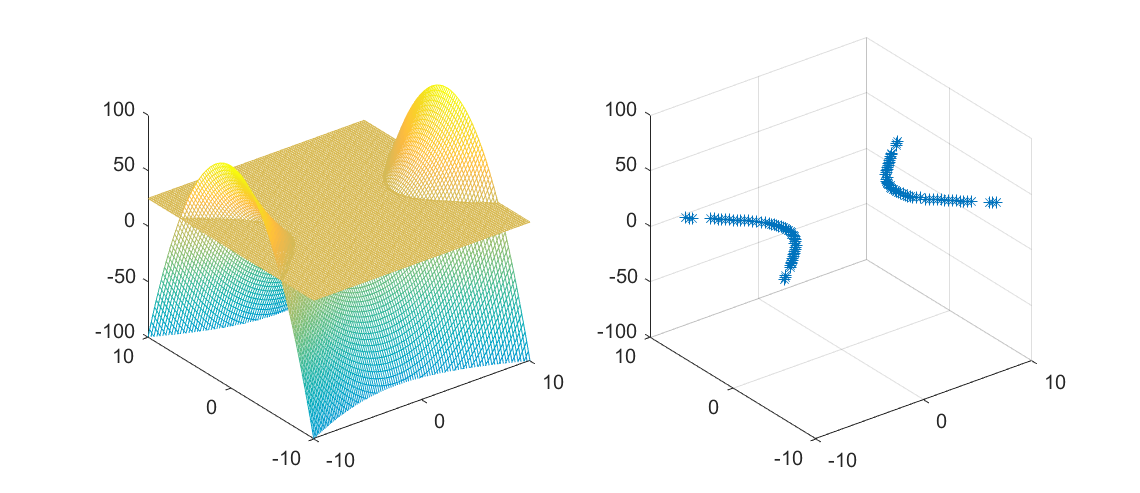
例5分析由函数z=x²-2y²构成的曲面形状及与平面z=a的交线。

程序如下：

[x,y]=meshgrid(-10:0.2:10);
z1=(x.^2-2*y.^2)+eps;       %第一个曲面坐标
a=input('a=?');
z2=a*ones(size(x));          %第二个曲面坐标
subplot(1,2,1)
mesh(x,y,z1);hold on;mesh(x,y,z2)           %分别画出两个曲面
v=[-10,10,-10,10,-100,100];axis(v);grid    %第一子图的坐标设置
hold off
r0=abs(z1-z2)<=1;                        %求两曲面z坐标差小于1的点
xx=r0.*x;yy=r0.*y;zz=r0.*z2;        %求这些点上的x、y、z坐标，即交线坐标
subplot(1,2,2)
plot3(xx(r0~=0),yy(r0~=0),zz(r0~=0),'*')   %在第二子图画出交线
axis(v);grid       %第二子图的坐标设置

程序运行时，若输入a=25, 所得三维曲面图与交线如图所示。输入的a不同，曲面的交线就不同。

此外，还有两个和mesh 函数相似的函数，即带等高线的三维网格曲面函数meshc 和带底座的三维网格曲面函数 meshz 。 其用法与mesh 类似，不同的是meshc还在xy平面上绘制曲面在z 轴方向的等高线 meshz还在xy 平面上绘制曲面的底座。

函数surf 也有两个类似的函数，即具有等高线的曲面函数 surfc 和具有光照效果的曲面函 数 surfl。

例6 在xy 平面内选择区域[-8,8]×[-8,8],绘制函数

$$z=\frac{sin\sqrt{x^2+y^2}}{\sqrt{x^2+y^2}}$$
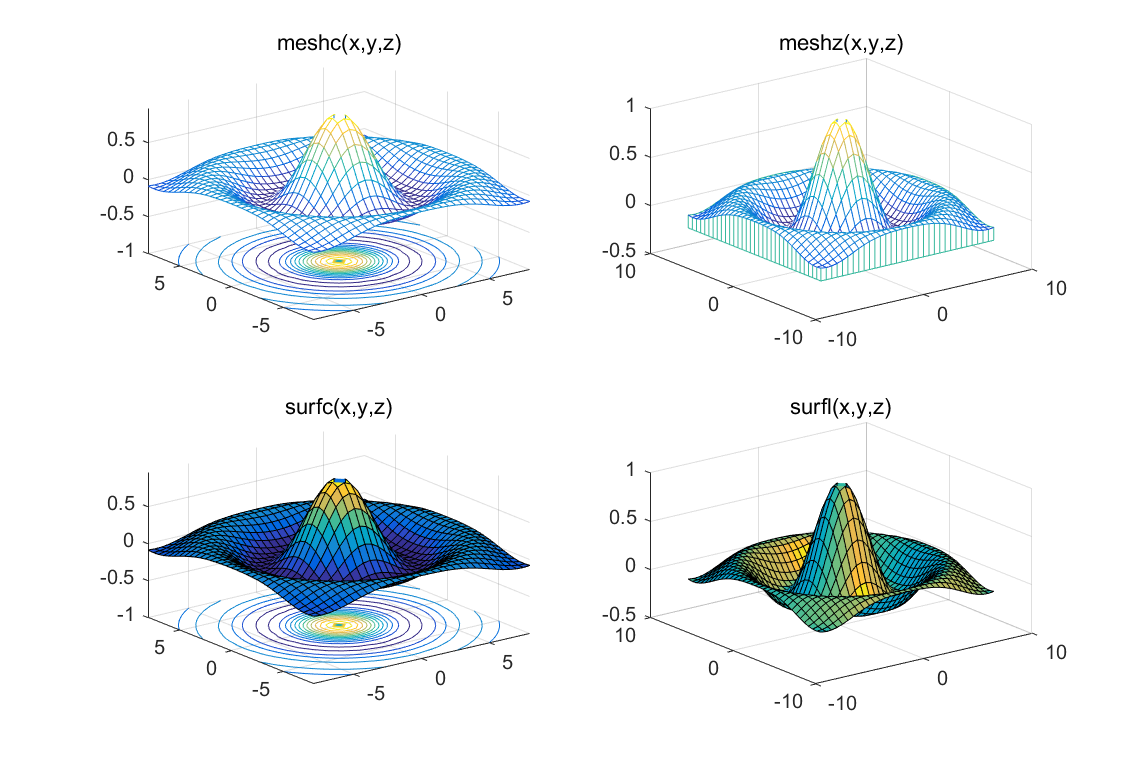
的4种三维曲面图(墨西哥帽子图形)。

程序如下：

[x,y]=meshgrid(-8:0.5:8);
z=sin(sqrt(x.^2+y.^2))./sqrt(x.^2+y.^2+eps);
subplot(2,2,1)
meshc(x,y,z)
title('meshc(x,y,z)')
subplot(2,2,2)
meshz(x,y,z)
title('meshz(x,y,z)')
subplot(2,2,3)
surfc(x,y,z)
title('surfc(x,y,z)')
subplot(2,2,4)
surfl(x,y,z)
title('surfl(x,y,z)')

程序运行结果如图所示。

3.标准三维曲面

MATLAB 提供了一些函数用于绘制标准三维曲面，还可以利用这些函数产生相应的绘图数据，常用于三维图形的演示。例如，sphere 函数和cylinder函数分别用于绘制三维球面和柱面。

sphere函数的调用格式如下：

[x,y,z]=sphere(n)

该函数将产生(n+1)×(n+1) 矩阵 x 、y 、z, 采用这3个矩阵可以绘制出圆心位于原点、半径 为1的单位球体。若在调用该函数时不带输出参数，则直接绘制所需球面。n 决定了球面的圆 滑程度，其默认值为20。若n 值取得较小，则将绘制出多面体表面图。

cylinder函数的调用格式如下：

[x,y,z]=cylinder(R,n)

其中，R 是一个向量，存放柱面各个等间隔高度上的半径，n 表示在圆柱圆周上有n个间隔点， 默认有20个间隔点。例如：

>>cylinder(3)

将生成一个圆柱。

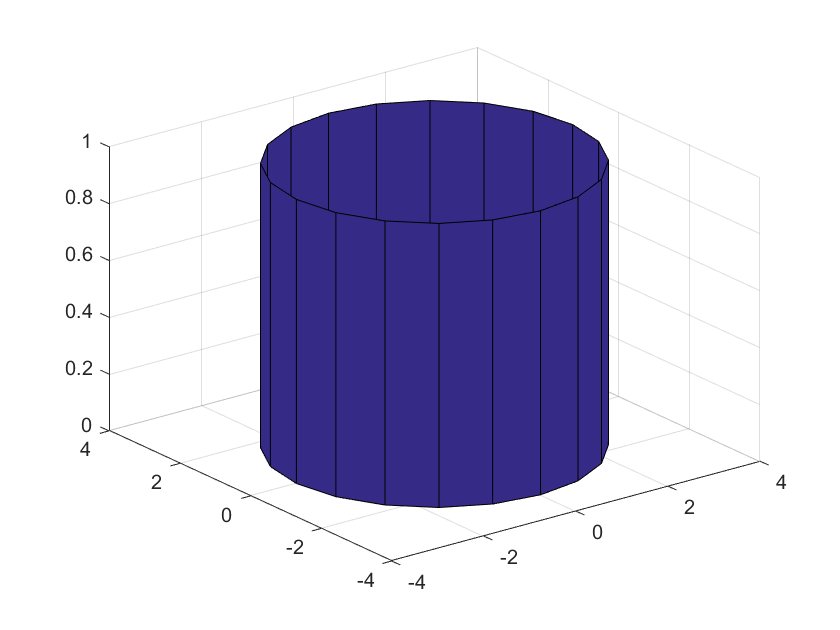
又如：

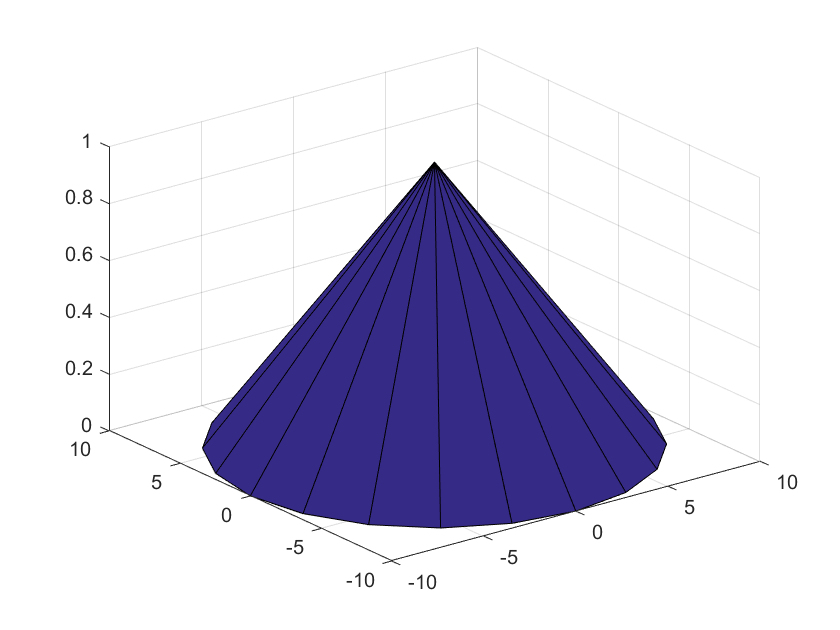
>>cylinder([10,0])

将生成一个圆锥

而执行下列命令：

>>t=0:pi/100:4*pi; 
>>R=sin(t);
>>cylinder(R,30)

将生成一个正弦型柱面。

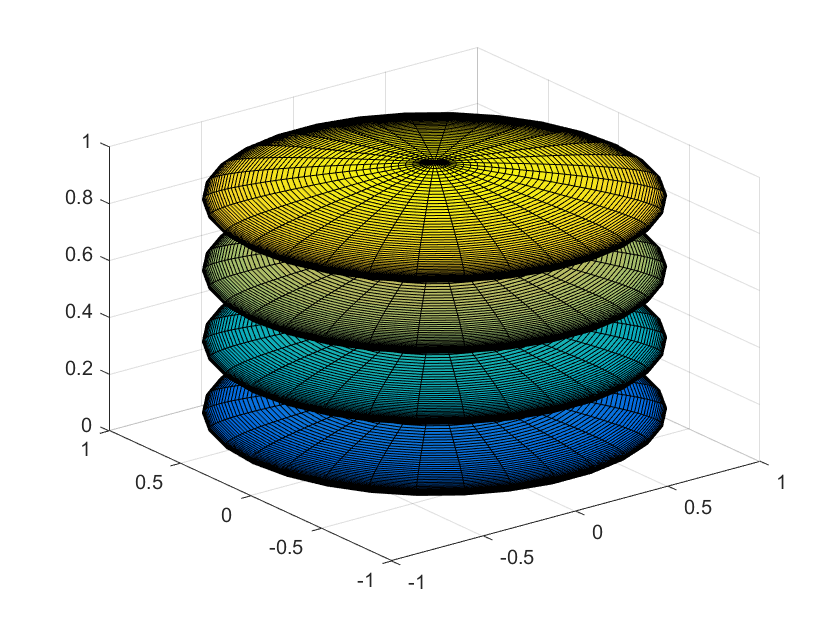
另外，生成矩阵的大小与R向量的长度及n 有关。其余用法与sphere 函数相同。

MATLAB还有一个 peaks 函数，称为多峰函数，常用于三维曲面的演示。该函数可以用来生成绘图数据矩阵，矩阵元素由以下函数在矩形区域[-3,3]×[-3,3]的等分网格点上的函数值确定。

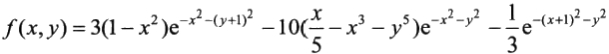
例如：

>>z=peaks(30);

将生成一个30×30矩阵z,即分别沿x 和y 方向将区间[-3,3]等分成29份，并计算这些网格点 上的函数值。默认的等分数是48,即p=peaks 将生成一个49×49矩阵p。也可以根据网格坐标 矩阵x 、y重新计算函数值矩阵。例如：

>>[x,y]=meshgrid(-5:0.1:5); 
>>z=peaks(x,y);

生成的数值矩阵可以作为mesh 、surf 等函数的参数而绘制出多峰函数曲面图。另外，若在调用 peaks 函数时不带输出参数，则直接绘制出多峰函数曲面图。

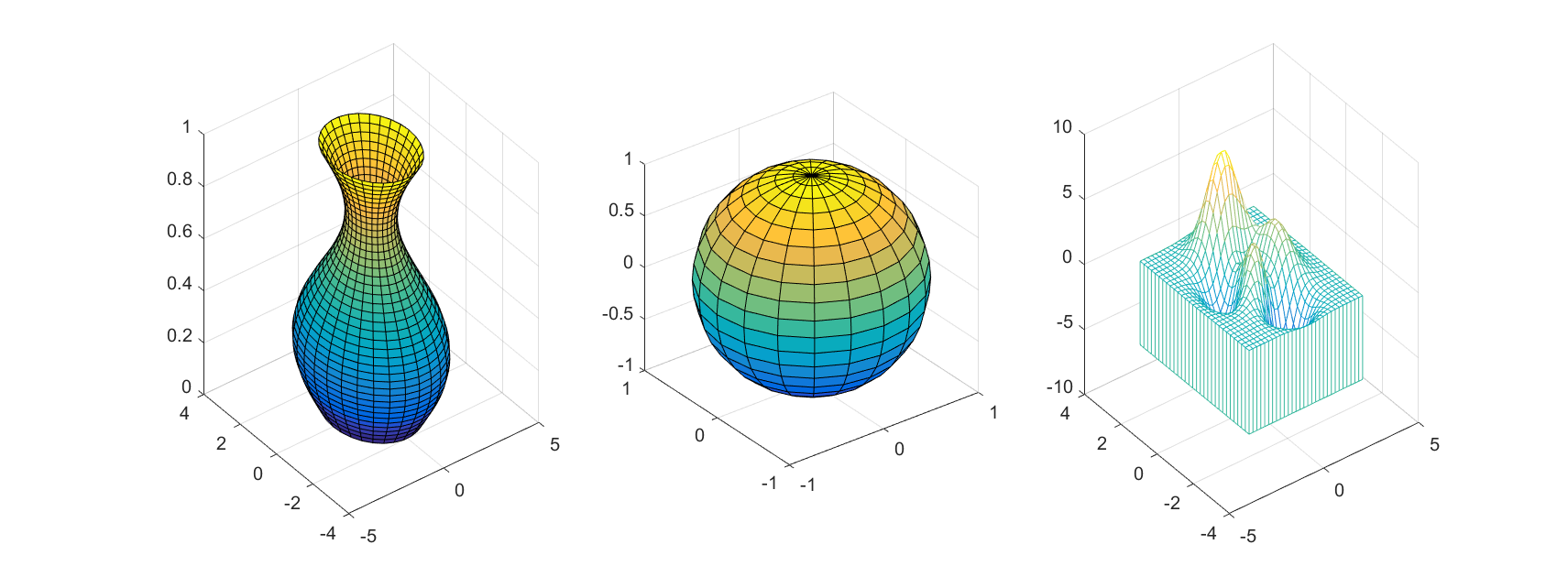
例6 绘制标准三维曲面图形。

程序如下：

t=0:pi/20:2*pi;
[x,y,z]=cylinder(2+sin(t),30);
subplot(1,3,1);surf(x,y,z)    %生成一个正弦型柱面
[x,y,z]=sphere;
subplot(1,3,2);surf(x,y,z);axis equal    %生成一个球面
[x,y,z]=peaks(30);
subplot(1,3,3);meshz(x,y,z)   %生成一个多峰曲面

三、其他三维图形

在介绍二维图形时，曾提到各种特殊图形，有些还可以以三维形式出现，使用的函数包括 bar3、bar3h、pie3 、fill3 、scatter3 、stem3和 quiver3。

1.三维条形图

bar3 函数绘制三维条形图，常用格式如下：

bar3(y)

bar3(x,y)

在第一种格式中，y 的每个元素对应于一个条形。第二种格式在x 指定的位置上绘制y 中 元素的条形图。

bar3h的用法与bar3 相同。

2.三维饼图

pie3 函数绘制三维饼图，常用格式如下：

pie3(x,explode)

其中x 为向量，用x 中的数据绘制一个三维饼图，explode设置相应的扇形是否偏离整体图形。

3.三维实心图

fill3 函数可在三维空间内绘制出填充过的多边形，常用格式如下：

fill3(x,y,z,c)

使用x 、y 、z 作为多边形的顶点，而c 指定了填充的颜色。

4.三维散点图

scatter3 函数可在三维空间内绘制出散点图，常用格式如下：

scatter3(x,y,z,c)

其 中 ，x 、y 、z 必须是等长度的向量，c 指定了填充的颜色。

5.三维杆图

stem3 函数绘制离散序列数据的三维杆图，常用格式如下：

stem3(z)

stem3(x,y,z)

第一种格式将数据序列z 表示为从xy 平面向上延伸的杆图，x 和 y 自动生成。第二种格式 在x 和 y 指定的位置上绘制数据序列z 的杆图。

6.三维箭头图

quiver3函数绘制三维空间的矢量图，常用格式如下：

quiver3(x,y,z,u,v,w)

其 中 ，x 、y 、z 、u 、v 、w 必须长度一样，绘制三维矢量图。矢量由(u,v,w)决定，所在位置由(x, y,z) 决定。例如，quiver3(1,2,3,4,5,6)以(1,2,3)为起点绘制一个矢量，即一个由(1,2,3)指向(4,5,6) 的箭头。

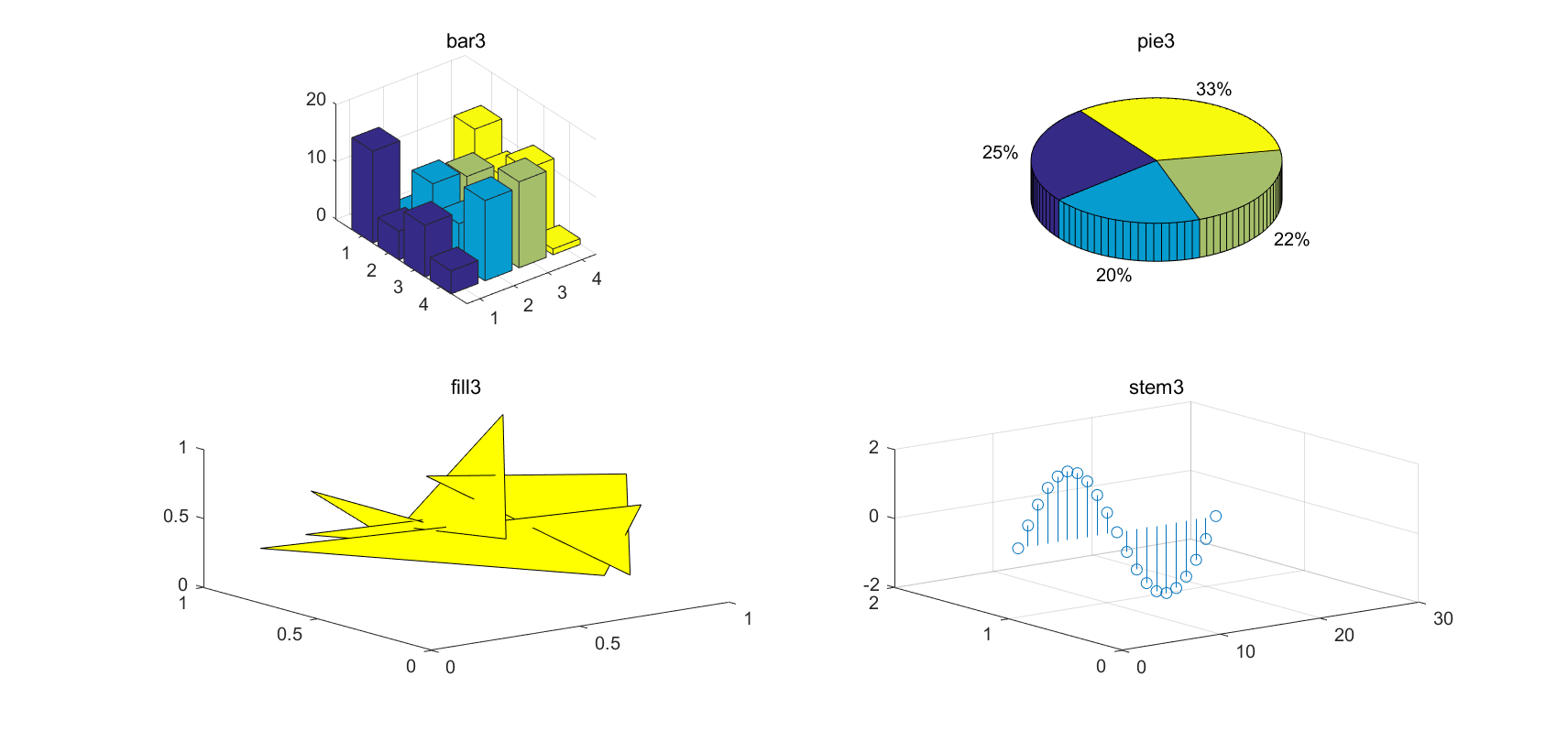
例7 绘制以下三维图形。

(1)绘制魔方阵的三维条形图。

(2)已知x=[2347,1827,2043,3025], 绘制三维饼图。

(3)用随机的顶点坐标值画出5个黄色三角形。

(4)以三维杆图形式绘制曲线y=2sin x。

程序如下：

subplot(2,2,1);bar3(magic(4));title('bar3')
subplot(2,2,2);pie3([2347,1827,2043,3025]);title('pie3')
a=rand(3,5);b=rand(3,5);c=rand(3,5);
subplot(2,2,3);fill3(a,b,c,'y');title('fill3')
y=2*sin(0:pi/10:2*pi);
subplot(2,2,4);stem3(y);title('stem3')

7.瀑布图、三维曲面的等高线图

绘制瀑布图用 waterfall函数，它的用法及图形效果与meshz 函数相似，只是它的网格线是在x 轴方向出现，具有瀑布效果。

等高线图分二维和三维两种形式，分别使用函数contour和 contour3绘制。

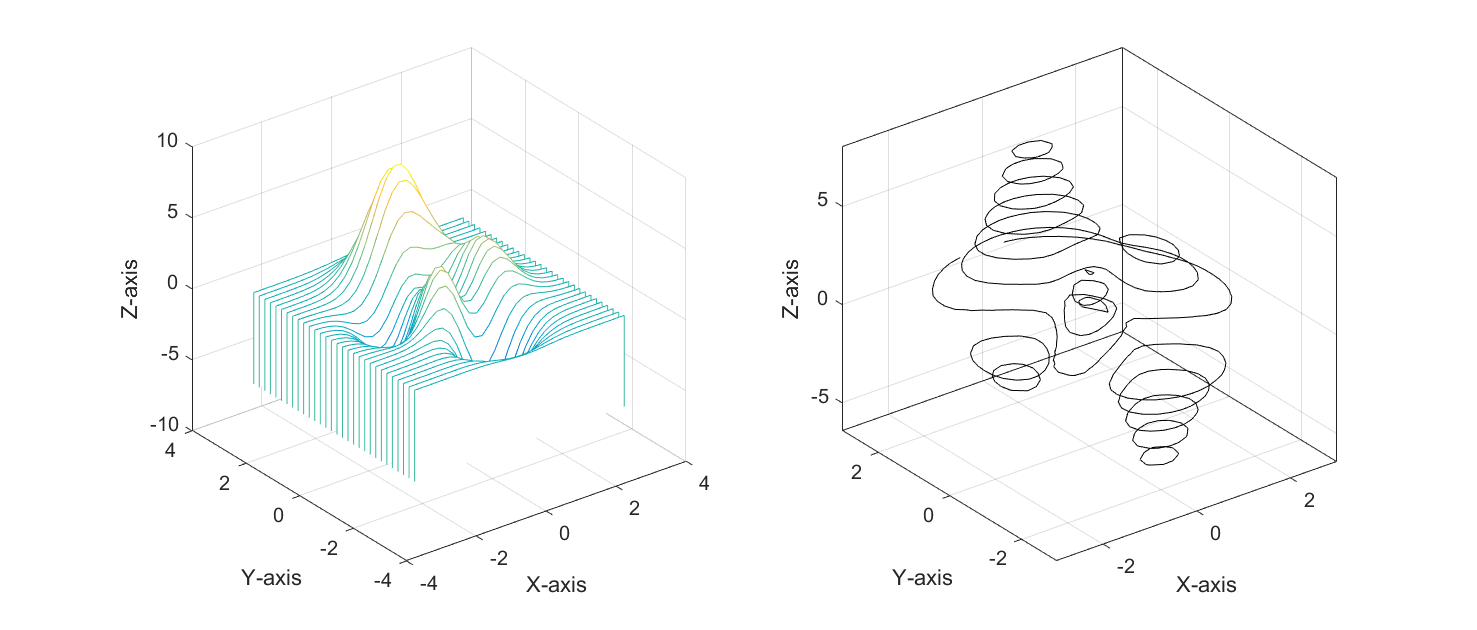
例8 绘制多峰函数的瀑布图和等高线图。

程序如下：

[X,Y,Z]=peaks(30);
subplot(1,2,1);waterfall(X,Y,Z)
xlabel('X-axis'),ylabel('Y-axis'),zlabel('Z-axis')
subplot(1,2,2);contour3(X,Y,Z,12,'k')     %其中12代表高度的等级数
xlabel('X-axis'),ylabel('Y-axis'),zlabel('Z-axis')