概率论笔记

最新推荐文章于 2025-04-13 17:20:13 发布

JK Chen

最新推荐文章于 2025-04-13 17:20:13 发布

阅读量3.5k

点赞数 7

分类专栏：学习笔记or周记or赛后总结

本文链接：https://blog.csdn.net/jk_chen_acmer/article/details/82770326

版权

学习笔记or周记or赛后总结专栏收录该内容

16 篇文章

订阅专栏

样本与事件

样本空间： 随机实验E的所有可能结果的集合S

样本点： 每个可能结果

随机事件： S的所有子集

基本事件：单个点组成的事件
必然事件：S本身
不可能事件：空集

事件之间的关系：

相等：互相包含
和事件：A并B
积事件：A交B
差事件：A减B
互斥：积事件为空集
对立：互斥且和事件为S
$\;\\\;$

$\;\\\;$
概率性质

非负：大于等于0
规范：P(S)=1，P(空集)=0
可列可加：互斥事件的概率和为其和事件的概率
容斥：B≥A，则P(B-A)=P(B)-P(A)
逆事件：AB互逆，P(A)+P(B)=1
加法：P(A∪B)=P(A)+P(B)-P(AB)
$\;\\\;$

$\;\\\;$
古典概型

等可能概型，基本事件概率相同

公式： P(A)=K（A中的基本事件数) / N（S中的基本事件数)

此方法可以绕过概率这一说法，变成统计事件的数量

例1：（取球问题）

a个白球，b个红球，k个人不放回得取球，求第i个人取到白球（A）的概率

N：前i个人取球的基本事件数为 $(a + b) * (a + b - 1) \dots (a + b - i + 1)$
K：前i个人取球第i个人取到白球的概率为 $a * (a + b - 1) * \dots (a + b - i + 1)$

$\therefore P(A)=a/(a+b)$

也就是说，放不放回第i个人取到白球的概率是一样的，当然，i要小于等于a+b

例2：（正品问题）

400件次品，1100件正品，求抽出100件90件为次品的概率

N：抽出100件的事件数为 $C_{1500}^{100}$
K：抽出90件次品的事件数为 $C_{400}^{90}C_{1100}^{10}$

$\therefore P(A)=\dfrac{C_{400}^{90}C_{1100}^{10}}{C_{1500}^{100}}$

$\;\\\;$

$\;\\\;$
条件概率

$P (A ∣ B)$ 表示在B事件发生的条件下A发生的概率

区别： 求AB同时发生的概率 $P (A B)$ ；而已知A发生，求B发生的概率 $P (B ∣ A)$

公式： $P(A|B)=\frac{P(AB)}{P(B)}，P(AB)=P(B)*P(A|B)=P(A)*P(B|A)$

乘法定理： $P(A_1A_2A_3...A_n)=P(A_1)*P(A_2|A_1)*P(A_3|A_1A_2)*...P(A_n|A_1A_2...A_{n-1})$
$\;\\\;$

$\;\\\;$
全概率公式

划分： $B_1,B_2...B_n$ 为样本空间 $S$ 的事件，且交集为S，两两互斥，则称 $B_1,B_2...B_n$ 为 $S$ 的一个划分

公式：（任意事件A）
$P(A)=P(A|B_1)P(B_1)+...P(A|B_n)P(B_n)$

应用： 当直接求A的概率不好求时，可能找到S的一个划分，如果 $P(A|B_i)$ 和 $P(B_i)$ 好求的话

贝叶斯公式

$P(B_i|A)=\frac{P(A|B_i)P(B_i)}{P(A|B_1)P(B_1)+...P(A|B_n)P(B_n)}$

将上述两个公式的n代为2，则变成：
$P(A)=P(A|B)P(B)+P(A|\overline B)P(\overline B)$
$P(B|A)=\frac{P(A|B)P(B)}{P(A|B)P(B)+P(A|\overline B)P(\overline B)}$

$\;\\\;$

独立性

若 $P (B ∣ A) = P (B)$ ，显然A事件和B事件互不影响，称A与B独立

推得：

$P (A) P (B) = P (A B)$
若A与B独立，那么 $\overline A与B，\overline B与A，\overline A与\overline B$ 独立

区分：

独立是指互不影响，有 $P (A B) = P (A) * P (B)$
而互斥是指不能同时发生，有 $P (A + B) = P (A) + P (B)$

$\;\\\;$

随机变量

将样本空间S中的所有元素e与一个实数对应，用函数X转换，称X=X(e)为随机变量

例如： 投3次硬币，正面次数为1的有100，010，001，那么X(001)=X(010)=X(001)=1

上述离散型随机变量X的分布律为：P(0)=1,p(1)=3,p(2)=3,p(3)=1，或是写出表格：

X	0	1	2	3
P	1	3	3	1

一：（0—1）分布

X	0	1
P	1-p	p

二：二项分布

一次伯努利试验相当于01分布，n次就是二项分布

X	k	…
P	$C_n^k p^k(1-p)^{n-k}$	…

称X服从参数为n，p的二项分布，记作：X~b(n,p)

三：泊松分布

使二项分布的P在 $\lim_{n\to\infty}$ 时，得到一下公式，其中 $\lambda$ 为>0常数

X	k	…
P	$\frac{\lambda^{k}e^{-\lambda}}{k!}$	…

称X服从参数λ的泊松分布，记作：X~ $\pi(λ)$

分布函数： 对于分布律做一个前缀和即为分布函数，显然有：
$P(x_1<X<=x_2)=P(X<=x_2)-P(X<=x_1)=F(x_2)-F(x_1)$

$\;\\\;$

连续性随机变量及其概率密度

f(x)为概率密度，其前缀和F(x)也叫分布函数（f(x)其实也就是概率而已）

例如： $\quad\quad(0<=x<3)\quad\\\quad\quad \qquad\;\;=2-\frac{x}{2}\quad(3<=x<=4)\\\quad\quad \qquad\;\;=0\quad\quad\quad(other)$

那么： $F(x)=0\quad\qquad\qquad\qquad\qquad\qquad(x<0)\\\qquad\qquad\quad=\int_0^x x/6dx \quad\quad\qquad\qquad\quad\;\,(0<=x<3)\quad\\\quad\quad \qquad\;\;\;=\int_0^3 x/6dx+\int_3^x (2-\frac{x}{2})dx \quad(3<=x<=4)\\\quad\quad \qquad\;\;\;=1\qquad\qquad\qquad\qquad\qquad\quad\,(x>4)$

性质：

$f (x) > 0$
$\int_{-\infty}^\infty f(x)dx=1$
$P(x_1<x<=x_2)=P(x_1<=x<x_2)=P(x_1<=x<=x_2)=P(x_1<x<x_2)$
$P(x_1<x<=x_2)=F(x_2)-F(x_1)=\int_{x_1}^{x_2}f(x)dx$
$F^{'}(x)=f(x)$
连续型随机变量 $P (A) = 0$ 不一定A为不可能事件

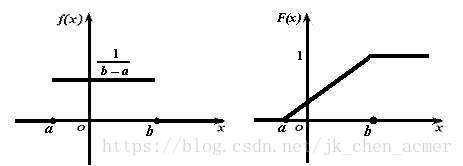
一：均匀分布

$f(x)=\frac{1}{b-a}\quad (a<x<b)\\ \quad\quad\;=0 \quad\quad(other)\\\;\\\to X$ ~ $U (a, b)$

$F(x)=0\quad\quad(x<a)\\\quad\quad\;=\frac{x-a}{b-a}\quad(a<=x<b)\\\quad\quad\;=1\quad\quad\,(x>=b)$
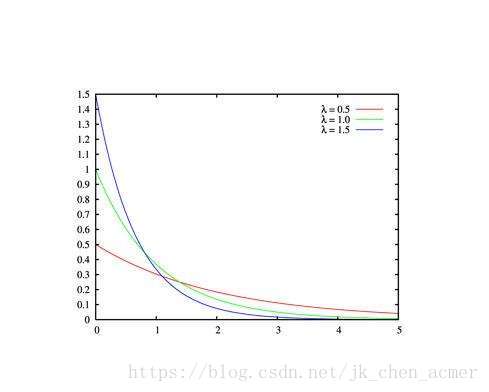
在这里插入图片描述
二：指数分布

$f(x)=\frac{1}{\theta}e^{-x/\theta}\quad (x>0)\\ \quad\quad\;=0 \quad\qquad\;(other)\\\;\\\to X满足参数为\theta的指数分布$

$F(x)=1-e^{-x/\theta}\quad (x>0)\\ \quad\quad\;=0 \quad\qquad\quad\;(other)$
在这里插入图片描述
三：正态分布

$f(x)=\dfrac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\eta)^2}{2\sigma^2}}\quad (-\infty<x<\infty)\\\;\\\to X$ ~ $N(\eta,\sigma^2)$

$F(x)=\dfrac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^x e^{-\frac{(x-\eta)^2}{2\sigma^2}}dt\quad (-\infty<x<\infty)$

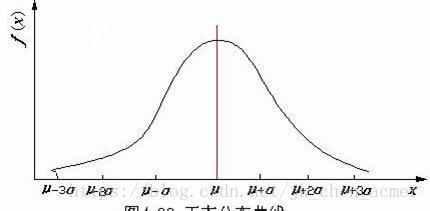
在这里插入图片描述
对称轴 $x = u$ ，倾斜度 $\frac{1}{\eta}$

当 $\eta=0,\sigma=1，为标准正态分布：\\\varphi(x)=\dfrac{1}{\sqrt{2\pi}}e^{-x^2/2}\\\Phi(x)=\dfrac{1}{\sqrt{2\pi}}\int_{-\infty}^x e^{-t^2/2}dt$

$\Phi(-x)=1-\Phi(x)$

正态分布的引理：

若： $X$ ~ $N(\eta,\sigma^2)$

$F(x)=P(X<=x)=\Phi(\dfrac{x-\eta}{\sigma})$
$P(x_1<X<x_2)=F(x_2)-F(x_1)=\Phi(\dfrac{x_2-\eta}{\sigma})-\Phi(\dfrac{x_1-\eta}{\sigma})$

做题时 $\Phi(x)$ 可以查正数部分表，负数部分可以 $\Phi(-x)=1-\Phi(x)$ 转化成正数

$\;\\\;$

随机变量的函数的分布

随机变量X的函数Y：

给出随机变量X的概率密度为 $f_X(x)=x/8,(0<x<4)$ ，求随机变量Y=2X+8的概率密度

$F_Y(y)=P\{Y<=y\}=P\{2X+8<=y\}=F_X((y-8)/2)$
$f_Y(y)=F_Y(y)^{'}\\=f_X((y-8)/2)*((y-8)/2)^{'}\\=\frac{1}{8}(y-8)/2/2，(8<y<16)$

定理：

可以 $a=-\infty,b=\infty$

若f(x)在[a,b]单调，不在[a,b]等于0，y=g(x)，h(y)为g(x)的反函数，有：

$f_Y(y)=f_X(h(y))*|h(y)^{'}|,\alpha<y<\beta\\\;\;\;\qquad=0,其他$

$\alpha=min(g(a),g(b)),\beta=max(g(a),g(b))$

$\;\\\;$

二维随机变量

$F(x,y)=P\{X<=x,Y<=y\},开口向左下的矩形$

显然： $F(-\infty,x)=F(x,-\infty)=0,F(\infty,\infty)=1$

二维的分布律称为联合分布律

$P\{(X,Y)\in G\}=\iint_Gf(x,y)dxdy$

$\dfrac{\vartheta^2F(x,y)}{\vartheta x\vartheta y}=f(x,y)$

例题：

若 $0 < x < 4, 0 < y < 6$ ，那么 $P\{x+y<4\}=\int_{0}^6\int_{0}^{4-y }f(x,y)dxdy$

$\;\\\;$

边缘分布

让 $Y\to\infty$ ，(X,Y)的分布律就变成了X的分布律

离散型：（边缘分布律）
$p_{i·}=\sum_{j=1}^{\infty}p_{ij}$
$p_{·j}=\sum_{i=1}^{\infty}p_{ij}$

连续型：（边缘概率密度）
$f_X(x)=\int_{-\infty}^{\infty}f(x,y)dy$
$f_Y(y)=\int_{-\infty}^{\infty}f(x,y)dx$

计算时，将 $-\infty和\infty$ 换成使 $f(x,y)\not=0$ 的上下限即可

例如： $f(x,y)=6 , x^2<=y<=x$

$f_X(x)=\int_{x^2}^x6dy=6(x-x^2),(0<=x<=1)$

$f_Y(y)=\int_{y}^{\sqrt{y}}6dx=6(\sqrt{y}-y),(0<=y<=1)$

$\;\\\;$

条件分布

$P\{X=x_i|Y=y_j\}=\dfrac{P\{X=x_i,Y=y_j\}}{P\{Y=y_j\}}=\dfrac{p_{ij}}{p_{.j}}$

$P\{X=x_i|Y=y_j\}=\dfrac{p_{ij}}{p_{.j}}，i=1,2\dots$ 称为 $X$ 在 $Y_j$ 下的条件分布律

公式： $f_{X|Y}(x|y)=f(x,y)/f_Y(y)$

$\;\\\;$

相互独立

公式： $f(x,y)=f_X(x)f_Y(y)$

若 $X, Y$ 相互独立， $F (X), G (Y)$ 相互独立

$\;\\\;$

函数的分步

$Z = X + Y$
$f_{X+Y}(z)=\int_{-\infty}^{+\infty}f(z-y,y)dy$
$f_{X+Y}(z)=\int_{-\infty}^{+\infty}f(x,z-y)dx$

$\quad Z=XY$
$f_{Y/X}(z)=\int_{-\infty}^{+\infty}|x|f(x,xz)dx$
$f_{XY}(z)=\int_{-\infty}^{+\infty}\frac{1}{|x|}f(x,z/x)dx$

$Max\quad Min$
$F_{max}(z)=F_X(z)F_Y(z)$
$F_{min}(z)=1-[1-F_X(z)][1-F_Y(z)]$