HDU—2604 Queuing

Description

Queues and Priority Queues are data structures which are known to most computer scientists. The Queue occurs often in our daily life. There are many people lined up at the lunch time. 

  Now we define that ‘f’ is short for female and ‘m’ is short for male. If the queue’s length is L, then there are 2 L numbers of queues. For example, if L = 2, then they are ff, mm, fm, mf . If there exists a subqueue as fmf or fff, we call it O-queue else it is a E-queue. 
Your task is to calculate the number of E-queues mod M with length L by writing a program. 

 

Input

Input a length L (0 <= L <= 10 6) and M.

 

Output

Output K mod M(1 <= M <= 30) where K is the number of E-queues with length L.

 

Sample Input

3 8

4 7

4 8

 

Sample Output

6

2

1

 

【分析】

题意：长度为L的字符串，每一位可以填'f'或'm'，如果某个字符串中任意相邻的三个字符组成了"fmf"或"fff"就是所谓O队列，不存在O队列的字符串被称为E队列，现在问长度为L的E队列有多少种，答案取模M

首先肯定考虑dp，显然状态是可以递推的

设dp[n]表示长度为n的E序列的方案数，那么考虑什么状态可以转移到dp[n]

第n位可以放的字符分别为'f'和'm'

1.若放'm'，那么对前面n-1的序列没有任何限制，则dp[n-1]可以全部转移过来，则 +dp[n-1]

2.若放'f'，那么对前面的序列就有要求了，那么再考虑往前一位到达[n-1]，

   可以发现不管f[n-1]填'f'还是'm'都不能确定，因为都有可能组成O队列

   所以再往前考虑一位到达[n-2]

    若[n-1]填'm'，那么[n-2]只能填'm'，那么在这个情况下所有dp[n-3]都是满足条件的状态，则 +dp[n-3]

    若[n-1]填‘f’，那么[n-2]只能填'm'，在这个情况下并不是所有dp[n-3]都是满足的状态因为[n-3]不能填'f'，也就是[n-3]只能填'm'，      那么在这个情况下，所有dp[n-4]都是满足条件的状态，则 +dp[n-4]

以上

那么就解决了递推的问题

dp[n] = dp[n-1] + dp[n-3] + dp[n-4]

那么因为每次取模数都不一样，所以不能预处理...虽然时间上可以预处理也就是30*1000000，但是要记录的话就会MLE了...

所以考虑矩阵快速幂，这里借用网上的矩阵图

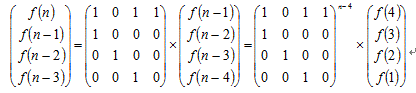
【代码】

#include <bits/stdc++.h>
using namespace std;
int n,MOD;
int a[6] = {1,2,4,6,9,15};
struct XX{
    int v[4][4];
    void init(){
    	memset(v,0,sizeof(v));
	    v[1][0] = v[0][0] = v[0][2] = 
		v[2][1] = v[3][2] = v[0][3] = 1;
	}
	void clear(){
		memset(v,0,sizeof(v));
	    for(int i = 0; i < 4; i ++)
	    	v[i][i] = 1;
	}
}x,s;

XX Mul(XX a,XX b){
    XX c;
    for(int i = 0; i < 4; i ++)
    for(int j = 0; j < 4; j ++){
        c.v[i][j] = 0;
        for(int k = 0; k < 4; k ++)
        	c.v[i][j] =(c.v[i][j] + (a.v[i][k] * b.v[k][j])%MOD ) % MOD;
    }
    return c;
}
void Matrix(int n)
{
    while(n){
        if(n & 1) x = Mul(x,s);
        n >>= 1;
        s = Mul(s,s);
    }
    int ans = 0;
    for(int i = 0; i < 4; i ++)
    	ans += (x.v[0][i] * a[4 - i])%MOD;
    printf("%d\n",ans%MOD);
}
int main()
{
    while(~scanf("%d%d",&n,&MOD))
    {
        if(n <= 4){
            printf("%d\n",a[n]%MOD);
            continue;
        }
        
        s.init();
        x.clear();
	    
        Matrix(n - 4);
    }
    return 0;
}