【2015の复活】Hopscotch——CDQ分治

Problem

Background

给定一个 n 行 m 列的方格,每个格子里有一个正整数 a,1 ≤ a ≤ k, k ≤ n ∗ m
假设你当前时刻站在 (i, j) 这个格子里,你想要移动到 (x, y),那必须满足以下三个条件
1:i < x
2:j < y
3:第 i 行第 j 列格子里的数不等于第 x 行第 y 列格子里的数
求从 (1, 1) 移动到 (n, m) 的不同的方案数

Input

第一行三个数 n, m, k
接下来 n 行每行 m 个正整数,表示每个格子里的数

Output

一行一个数,表示从 (1, 1) 移动到 (n, m) 的不同的方案数,模 10 9 + 7

Example

hopscotch.in
4
1
1
1
1
4
1
3
2
1
4
1
2
4
1
hopscotch.out
5
1
1
1
1

Scoring

• 对于 20% 的数据,n, m ≤ 20。
• 对于 60% 的数据,n, m ≤ 100。
• 对于 100% 的数据,n, m ≤ 750。

Solution

这道题rpeng曾经讲过，做法有很多，可持久化，哈希+数据结构都可以做，在这里介绍一个利用CDQ分治的做法。
首先，我们考虑一个60分的做法
$f_{i,j} = \sum f_{k,l} (x_{i,j} \neq x_{k,l})$
将这个式子转化为
$f_{i,j} = \sum f_{k,l} - \sum f_{p,q} (k < i, l < j, x_{i,j} = x_{p,q})$
这样题目就只需要快速的统计两个部分和，这就为优化转移提供了可能
我们发现，这个DP是自上而下的，第i行的状态需要从前i-1行转移过来，而第i行对前i-1行均不造成影响，这样就可以使用CDQ分治
我们在这里对行分治，用work(up,down)表示处理up~down区间。那我们最后要的得到的就是work(1,n)
当work(up,down)时，$mid = (l + r) / 2$，我们假设l~mid已经计算完毕，则可以用l~mid更新mid+1~down。我们不难想到用$sum$表示l~mid中的部分和，用$s_{k}$表示$\sum f_{i,j} (x_{i,j}=k)$，用$f_{i,j}$表示到达$(i,j)$的方案数，然后用下图的顺序进行更新。

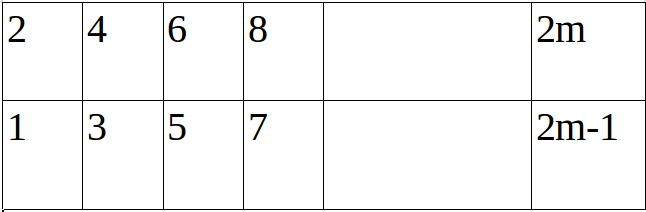
其中在奇数区域中，我们更新$f$数组，在偶数区域中，更新$sum$和$s$数组
那mid+1~down-1怎么转移到down呢？这里我们可以继续向下回溯，用work(mid+1,r)继续更新。
在每一层的更新中，s数组都需要清零。但若每次都memset肯定会超时。怎么办呢？可以用一个时间戳，给每一个$x_{i,j}$记一个$dfn_{x_{i,j}}$，当进入新的一层的更新时，将time_clock加一，在更新时，若发现$s_{x_{i,j}}\neq time\_clock$则将$s_{x_{i,j}}$清零并将$f_{i,j}$加入
最后分析时间复杂度。同一层分治中，每个区间只会被更新一次，所以每一层分治的总复杂度都是$NM$，而分治的层数不会超过$log_2N$层，所以总的时间复杂度是$O(NMlog_2N)$
完美解决了这个问题

Code

#include <bits/stdc++.h>
using namespace std;
#define rep(i, a, b) for(int i = (a); i <= (b); i++)
#define red(i, a, b) for(int i = (a); i >= (b); i--)
#define ll long long

const ll mod = 1000000007;
const int N = 800;
const int S = N * N;
ll x[N][N], f[N][N];
ll dfn[S], s[S];
int n, m, time_clock, num;
ll k;

inline ll read() {
    ll x = 0; char c = getchar();
    while(!isdigit(c)) c = getchar();
    while(isdigit(c)) {
        x = x * 10ll + c - '0';
        c = getchar();
    }
    return x;
}

void work(int l, int r) {
    int mid = (l + r) / 2;
    if (l == r) return;
    work(l, mid);
    ++time_clock; num = 0;
    rep(j, 1, m) {
        red(i, r, mid + 1) {
            if (dfn[x[i][j]] < time_clock) {
                dfn[x[i][j]] = time_clock;
                s[x[i][j]] = 0;
            }
            f[i][j] = (f[i][j] + num - s[x[i][j]] + mod) % mod;
        }
        rep(i, l, mid) {
            if (dfn[x[i][j]] < time_clock) {
                dfn[x[i][j]] = time_clock;
                s[x[i][j]] = 0;
            }
            s[x[i][j]] = (s[x[i][j]] + f[i][j]) % mod;
            num = (num + f[i][j]) % mod;
        }
    }
    work(mid + 1, r);
}

int main() {
    scanf("%d%d", &n, &m);
    k = read();
    rep(i, 1, n) rep(j, 1, n) x[i][j] = read();
    f[1][1] = 1;
    memset(s, 0, sizeof(s));
    work(1, n);
    cout << f[n][m] << endl;
    return 0;
}

写的最满意的一次题解啦！

End.