算法学习笔记（3）-- 树状数组

一、简介

前面学习了前缀和，可以进行区间的求和。

但是如果需要多次询问，每次询问修改某个数，并进行区间求和，就会达到O(Q * N)的复杂度，大多数情况下是会超时的。

树状数组就是一种可以在O(log(i))的时间下求出区间 [1, i] 的和数据结构。

二、原理

1.首先了解一下树状数组是如何进行区间求和的。

由前缀和，我们首先想到，求 [L, R] 的和，只需要用 [1, R] 的和 减去 [1, L - 1] 的和。那么同样的，在树状数组中，就是维护一个数组 C[i]，来记录 [1， i] 的和。

（1）那么如何维护这个数组呢，树状数组选择了将 i 转换为 二进制 的方式来把 [1, i] 分成多个区间进行维护。具体什么意思呢？

例如，i = 11，目的是求 [1, 11] 的区间和：

11 的二进制数是 1011，这个时候，会分别维护 (0000, 1000] 和 (1000, 1010] 和 (1010, 1011] 这三个区间。

（2）那么问题就来了，为啥是这三个区间呢？

我们注意到，这三个区间的右端点 1000、1010、1011，不就是11的二进制数1011从右往左依次去掉1的几个状态吗。

说到这里形势已经很明朗了，通过将 [1, i] 分为多个区间来维护，每个区间的左右端点通过不断去掉最低位的1来得出。

而0000、1000、1010这几个数，可以通过一个神奇的操作来得到，那就是lowbit(i)，它代表了二进制数最后一个1与剩下的0的值。比如：十进制的10的 lowbit(10) = 2 = 。

因此，区间的数量其实就等于二进制数中1的个数，这也是为什么复杂度为log的原因。

（3）这时候就会有聪明的同学发现了，诶那你这 C[i] 就不是 [1, i] 的和了呀。

没错，C[i] 实际上代表了 (i - lowbit(i), i] 这个区间的和，假设 i - lowbit(i) = x，那么下一个区间就是 (x - lowbit(x), x]。

比如 i = 8，ans = (0, 8]

比如 i = 7，ans = (6, 7] + (4, 6] + (0, 4]

比如 i = 6，ans = (4, 6] + (0, 4]

``````

到这里区间求和就讲完了，下面讲单点修改。

2.如何进行单点修改

假设我们修改了 a[i]，那么 C 中包含 节点i 的区间我们都要去维护。

注意哦，我说的是包含 节点i 的区间。

（1）咋知道哪些区间包含 节点i 呢？

首先，为了满足复杂度需求，单点修改的时间也应该是O(log(i))。

既然这样，考虑到在区间求和中使用了 lowbit() 这个神奇的操作，我们在单点修改中也想使用 lowbit() 这个操作。

区间求和的时候是不断减去 lowbit(i)，因为要查找 i 分成了哪些区间；现在单点修改，其实恰好就是不断加上 lowbit(i)，也恰好是这些区间包含了 i（其实具体为啥我也没搞懂）。

     

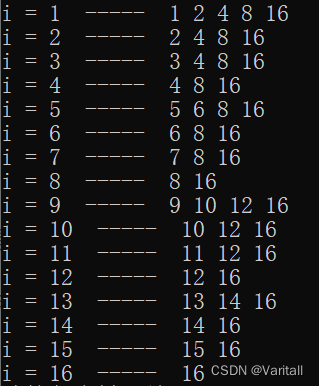
图一：选一个i，不断加上lowbit(i)；

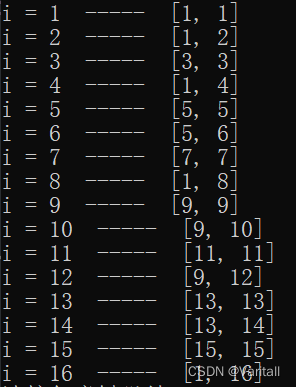
图二：选一个i，写出他的区间范围，即 C[i] 代表的区间；

我们可以随便看一个，比如 i = 7，在图二中去找哪些区间包含了 i = 7，发现恰好是7、8、16，与图一对应上了。

因为我自己还没搞懂这部分，就不多说了。

（2）找到区间之后呢？

找到区间之后，假设第 i 位上增大 x，那么直接给 C[i] += x 即可，然后继续找下一个区间，也就是继续lowbit，直到超出范围。

三、拓展

1.区间修改、单点查询

除了“单点修改、区间查询”这种操作，树状数组还可以“区间修改、单点查询”。

我们知道，对差分数组求前缀和，就能得到原数组。

如果我们将原数组变为差分数组，以这个差分数组来建树，那么在查询的时候求 [1, i] 的区间和，不就相当于求 [1, i] 的前缀和吗，而 [1, i] 的前缀和，不就是点 i 的值吗。

注意：

区间修改的时候记得要修改两个位置，一个是区间左端点，一个是区间右端点加一。

即：

modify(l, k);
modify(r + 1, -k);

四、例子

1.单点修改、区间查询：P3374 【模板】树状数组 1 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

AC代码：

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 7;

int n, m, p;
int a[maxn], t[maxn];

int lowbit(int x) { return x & -x; }

void modify(int x, int k) {
	for (int i = x; i <= n; i += lowbit(i)) t[i] += k;
}

int query(int x) {
	int ans = 0;
	for (int i = x; i != 0; i -= lowbit(i)) ans += t[i];
	return ans;
}

signed main() {
	cin >> n >> m;
	for (int i = 1; i <= n; ++i) cin >> a[i];
	for (int i = 1; i <= n; ++i) modify(i, a[i]);
	while (m--) {
		cin >> p;
		if (p == 1) {
			int x, k;
			cin >> x >> k;
			modify(x, k);
		}
		else if (p == 2) {
			int x, y;
			cin >> x >> y;
			cout << query(y) - query(x - 1) << '\n';
		}
	}
	return 0;
}

2.区间修改、单点查询：P3368 【模板】树状数组 2 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

AC代码：

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 7;

int n, m;
int a[maxn], pre[maxn], sub[maxn];

int lowbit(int x) { return x & -x; }

void modify(int x, int k) {
	for (int i = x; i <= n; i += lowbit(i)) pre[i] += k;
}

int query(int x) {
	int ans = 0;
	for (int i = x; i != 0; i -= lowbit(i)) ans += pre[i];
	return ans;
}

signed main() {
	cin >> n >> m;
	for (int i = 1; i <= n; ++i) cin >> a[i];
	for (int i = 1; i <= n; ++i) sub[i] = a[i] - a[i - 1];	//差分数组
	for (int i = 1; i <= n; ++i) modify(i, sub[i]);		//以差分数组建树
	while (m--) {
		int t; cin >> t; 
		if (t == 1) {
			int x, y, k;
			cin >> x >> y >> k;
			modify(x, k);
			modify(y + 1, -k);
		}
		else if (t == 2) {
			int x; cin >> x;
			cout << query(x) << '\n';
		}
	}

}