最小生成树 Kruskal+Prim算法【图论】

最新推荐文章于 2025-11-05 18:56:22 发布

原创最新推荐文章于 2025-11-05 18:56:22 发布 · 713 阅读

20 ·

CC 4.0 BY-SA版权

文章标签：

#图论 #c++ #算法

图论专栏收录该内容

4 篇文章

订阅专栏

简介

最小生成树是一种比较简单的图论题目，常用算法为两种贪心算法——Prim 和 Kruskal。本文将详细介绍这两个算法。

定义

什么是最小生成树？这个名字起的很高大上，其实定义很简单。我们假设有一张n个结点的无向图。我们需要找到一个n-1条现有边组成的集合，这个集合包含了所有点，连通且边权之和最小。

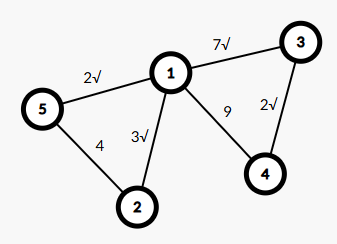
比如有一张5个结点的无向图如下：

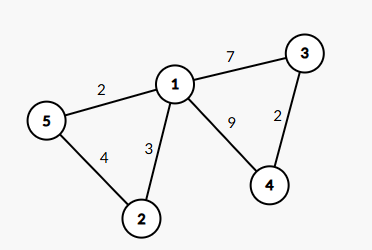
我们用从中找到四条边，这四条边需要连接起这5个点，并且权值和要最小。我们可以发现这里的最小生成树为：

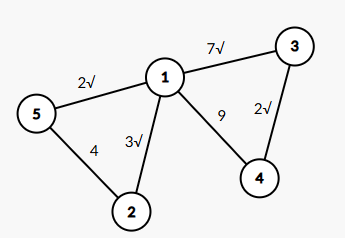
这里最小生成树的权值和为14.

Prim算法

Prim算法的核心其实是贪心，原理也很简单，就是每次找到最短的边。详细来说，Prim会先从任意一点开始，遍历与它相连的所有边，找出最小的加入联通块。同时用这个新点的相邻边的权值更新最小值，一直持续直到无法更新。注意不可以重复加入结点。

Prim的时间复杂度最大的瓶颈为查询最小值，和dijikstra一样，我们需要使用优先队列对查询最小值进行优化，这样可以把线性的查询变成log的。

示例

依旧使用上图，我们假设从1点开始。我们查询与1相连的边，发现权值最小为2。我们因此将5加入联通块：

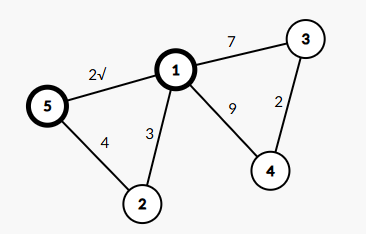
我们再找与联通块相连的所有边中最小的，发现1-2这条边的权值最小，我们加入2：

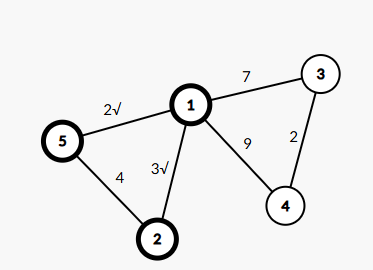
此时我们再次查询发现4是权值最小的，但是我们要注意到此时的5已经遍历过了，加这条边对生成树毫无意义，我们直接忽略，因此加入3：

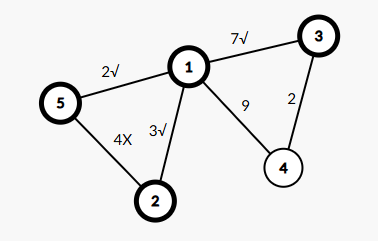
接下来加入4就可以了。

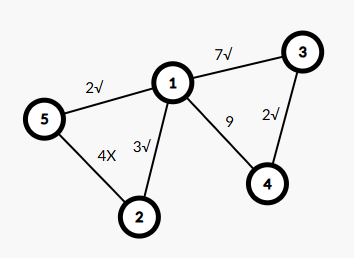
我们发现这与我们手推的最小生成树是一致的。

强烈推荐这篇文章

原理

其实很多人也可以注意到这个算法与dijikstra非常相似。同样的被求最小值硬控，同样的优先队列，但其实它们的原理也差不多。

这个算法看起来很容易就能举出反例，其中最常见的应该是如果我不选这条边而是从其他边绕过来会不会更优。但这是不可能的，因为如果想更优这条路线需要比当前路线到达快，而我们清楚想要从这个结点到其他结点的路线一定比最小边大，而最小边就指向要加入的点。通俗的说，这些方案输在了起跑线，你拼命的从其他地方绕过来，但是在第一步你就比对面的时间要晚。

代码实现以及例题

例题

代码：

#include <bits/stdc++.h>
#define int long long
using namespace std;//法1 prim+堆优化
const int N=5005;
int n,m,x,y,w,dis[N],ans;
bool f[N];
struct node{
	int u,d;
	bool operator < (const node &u) const{
		return u.d<d;
	}	
};
vector<node>v[N];
int prim(){
	priority_queue<node>q;
	for(int i=1;i<=n;i++) dis[i]=(1e17);
	dis[1]=0,q.push({1,0});
	while(q.size()){
		node t=q.top();
		q.pop();
		if(f[t.u]) continue;
		else f[t.u]=1,ans+=t.d;
		for(int i=0;i<v[t.u].size();i++){
			int u=v[t.u][i].u,w=v[t.u][i].d;
			if(dis[u]>w){
				dis[u]=w;
				q.push({u,dis[u]});
			}
		}
	}
	for(int i=1;i<=n;i++){
		if(!f[i]) return -1;
	}return ans;
}
signed main(){
	cin>>n>>m;
	while(m--){
		cin>>x>>y>>w;
		v[x].push_back({y,w});
		v[y].push_back({x,w});
	}
	if(prim()==-1) cout<<"orz";
	else cout<<prim();
	return 0;
}

这里的dis表示这个结点与父节点之间的距离。讲道理这个代码看上去还是很吓人的，因此写kruskal会更好些。

Kruskal算法

Kruskal算法其实也是贪心算法，但它的原理要粗暴的多。Kruskal算法会直接将所有的边排序，并判断是否需要连接，如果需要就用并查集合并两边，直至联通块个数为1。如果不知道并查集是什么可以看一下我的往期文章。

示例

一样的我们用之前那张图。首先我们排序所有边，可得：

1 5 2
3 4 2
1 2 3
2 5 4
1 3 7
1 4 9

（前两个表示边的连段，最后一个数表示边权）

我们对着图一一比对。首先第一条边肯定是直接加入就行：

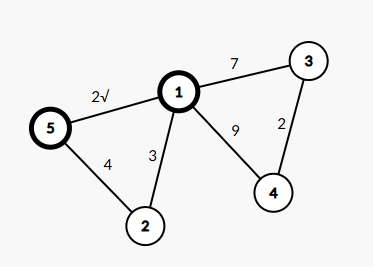
第二条第三条同理。

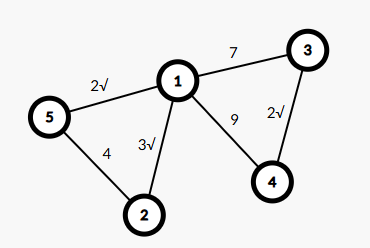
此时其实有两个联通块，（1,2,5）和（3,4），所以我们可以发现新的边2 5 4不能加入，因为两端的点属于一个联通块。我们直接跳过。此时我们加入1 3 7，联通块只有一个，程序结束。

答案正确。

原理

这个算法看起来也非常邪门，凭什么直接排序就可以求出最小生成树。感性理解一下，最小生成树肯定需要最小，同时因为是一棵树，每一条边都需要加入一个新点到树内，此时我们选择边权最小的边连接的新点没有问题吧？我们使用并查集可以有效避免加入旧点，因此这个算法一定是对的。

代码实现

这道题例题和上题一样，这里不放了。

代码：

#include <bits/stdc++.h>
#define int long long
using namespace std;//法2 kruskal
const int N=2e5+10,M=5e3+10;
int n,m,x,y,w,ans,sl,f[M];
struct node{
	int u,v,w; 	
}t[N];
bool cmp(node x, node y){
	return x.w<y.w;
}
int fa(int x){
	if(f[x]==x) return x;
	else return f[x]=fa(f[x]);
}
int krustal(){
	ans=0,sl=n;
	for(int i=1;i<=n;i++) f[i]=i;
	sort(t+1,t+m+1,cmp);
	for(int i=1;i<=m;i++){
		if(fa(t[i].u)!=fa(t[i].v)){
			f[fa(t[i].u)]=fa(t[i].v),ans+=t[i].w,sl--;
		}
		if(sl==1) return ans;
	}return -1;
}
signed main(){
	cin>>n>>m;
	for(int i=1;i<=m;i++) cin>>t[i].u>>t[i].v>>t[i].w;
	if(krustal()==-1) cout<<"orz";
	else cout<<krustal();
	return 0;
}

这个的代码就好理解多了。