图解最小生成树问题：Kruskal算法和Prim算法

LiAnyung

已于 2025-02-08 11:36:28 修改

阅读量1.8k

点赞数 35

文章标签：算法数据结构图论链表剪枝贪心算法

于 2025-02-07 23:26:30 首次发布

本文链接：https://blog.csdn.net/m0_74496615/article/details/145475747

版权

一、基础概念介绍

1. 图的基本概念

图（Graph）：由顶点（vertex）集合和边（edge）集合组成。顶点表示图中的实体，边表示顶点之间的连接关系。
有向图和无向图：在有向图中，边有方向，即从一个顶点指向另一个顶点；在无向图中，边没有方向，顶点之间的边是双向的。
边的权值（Weight）：边所关联的数据，可以代表距离、成本等实际含义。在最小生成树问题中，通常考虑的是带权图，即每条边都有一个权值。

2. 生成树（Spanning Tree）

定义：生成树是指一个连通图的极小连通子图，它包含图中所有的顶点，并且有尽可能少的边。对于具有n个顶点的连通图，生成树有n-1条边。
性质：
- 生成树是连通的，即图中任意两个顶点之间都有路径。
- 生成树中没有回路，如果向生成树中添加任意一条边，就会形成一个回路。
- 生成树中的边数比顶点数少1，例如有4个顶点的连通图，其生成树有3条边。

3. 最小生成树（Minimum Spanning Tree，MST）

定义：在连通的、带权的无向图中，一个最小生成树是生成树中所有边的权值之和最小的生成树。
例子：假设有一个城市之间的公路网，每个城市是顶点，公路是边，公路的长度是边的权值。我们需要修建一个道路系统，使得所有城市都连通，并且总修建路程最短，这就是求解最小生成树的问题。

4. 最小生成树的相关定理

切分定理（Cut Property）：对于图中的任意一种切分（将顶点分成两个不相交的非空集合），如果有一条横跨两个集合的边，其权值在所有横跨边中最小，那么这条边一定属于最小生成树。这就是最小生成树算法（如Kruskal算法和Prim算法）的基础。
最优子结构：最小生成树问题具有最优子结构的性质。也就是说，如果将图分成两个子图，每个子图的最小生成树的组合加上连接两个子图的最短边，可以构成整个图的最小生成树。

二、Kruskal算法

Kruskal算法（克鲁斯卡尔算法）是一种最小生成树算法，又称为“加边法”，适用于稀疏图中，它的核心思想是通过不断选择权值最小的边来构建生成树。

注：最小生成树中具有n个节点，n-1条边。最小生成树不一定唯一，但最小生成树的边权值和唯一。

1. 算法步骤

初始化：将所有边按照权值从小到大排序。
选择边：从权值最小的边开始，依次选择边，并检查该边是否连接了两个不同的连通分量。
合并分量：如果该边不形成环（即连接了两个不同的连通分量），则将其加入生成树，并将这两个分量合并为一个。
重复步骤 2 和 3：直到生成树包含所有节点或已选择的边数达到 n−1（其中 n 是节点的数量）。

2. 原理图解

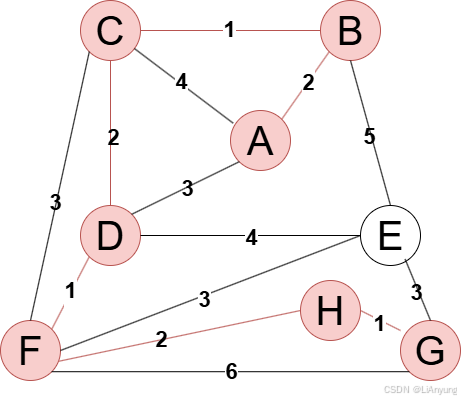
例如现在有一幅无向图，顶点为ABCDEFGH，边上数字表示边的权值。

Kruskal算法作为“加边法”，意为以“边”为核心，围绕“边”来进行记录。

为方便查询，也可以查看下列权值表：

	A	B	C	D	E	F	G	H
A		2	4	3
B			1		5
C				2		3
D					4	1
E						3	3
F							6	2
G								1
H

首先，将所有边按照权值从小到大排序。从权值最小的边开始，依次选择边。

图例中最小值为1，选择任意权值为1的边均可。这里我们选择BC边，刚开始生成树为空，与BC均不连通，所以BC边可以加入生成树中。

继续选择边，DF和HG均为1且与生成树均不连通，我们依次选择DF边和HG边。

上一轮选择完成后，得到如下的图例。

继续选择边，有多条权值为2的边：AB、CD、FH。

当选择AB边，A与生成树不连通（AB与原先生成树未成环），所以AB可以加入生成树；

当选择CD边，CD连通了ABC和DF两个不同的分量，因此可以CD加入生成树。

得到如下图例，继续选择FH边。

当选择EF边，和之前选择AB边一样，EF连通E和另一个不同的分量，因此EF可以加入生成树。

上一轮选择边结束得到如下图例。

接下来，继续选择权值为3的边： AD、CF、EF、EG。

当选择AD边，AD边连通的是同一个分量，结成环，因此舍去AD边；

当选择CF边，和前述原因相同，因此舍去CF边。

对于EF边和EG边，我们发现单独选择其中任意一条均满足条件，可以加入生成树中。事实上，这也对应了最小生成树不唯一的特点。这里我们选择EF边加入生成树，此时，所有顶点均已选取，边数也等于n-1（n为顶点数），程序结束。

得到最终的最小生成树，如下图所示：

树1

树2

上述两棵最小生成树均正确，符合最小生成树不唯一的特点，但最小生成树的权值和是唯一的，均为12。

3. 并查集

并查集（Union-Find）是 Kruskal 算法中的一个关键数据结构，用于高效地管理图的连通分量，并检测是否存在环。它通过支持两种操作：合并（Union）和查找（Find），来维护一组不相交的动态集合。

3.1 算法步骤

初始化：假如有n个元素，我们用一个数组或字典来存储每个元素的父节点。初始，我们先将它们的父节点设为自己。
Find 操作：查找某个节点的根节点，即它所属的集合的代表元素。
Union 操作：合并两个集，即将一个集合的根节点指向另一个集合的根节点。

3.2 Find函数

def find(parent: list, node: int) -> int:
    if parent[node] == node:  # 递归出口
        return node
    else:
        parent[node] = find(parent, parent[node])  # 路径压缩
        return parent[node]  # 向上查询

3.3 Union函数

def union(parent: list, u: int, v: int):
    root_u = find(parent, u)
    root_v = find(parent, v)
    parent[root_u] = root_v  # u的根节点指向v的根节点

4. 实现代码

# 测试数据 (u, v, weight)
testdata = [(1, 2, 2), (1, 3, 4), (1, 4, 3),
            (2, 3, 1), (2, 5, 5),
            (3, 4, 2), (3, 6, 3),
            (4, 5, 4), (4, 6, 1),
            (5, 6, 3), (5, 7, 3),
            (6, 7, 6), (6, 8, 2),
            (7, 8, 1)]
n = 8  # n为节点数

testdata.sort(key=lambda x: x[2])  # 初始化：按权值排序

parents = list(range(0, n + 1))  # 并查集初始化


def find(parent: list, node: int) -> int:
    if parent[node] == node:  # 递归出口
        return node
    else:
        parent[node] = find(parent, parent[node])  # 路径压缩
        return parent[node]  # 向上查询


def union(parent: list, u: int, v: int):
    root_u = find(parent, u)
    root_v = find(parent, v)
    parent[root_u] = root_v  # u的根节点指向v的根节点


result = []  # 记录边
sum = 0  # 记录权值和

for i in testdata:
    if find(parents, i[0]) != find(parents, i[1]):
        result.append(i)
        sum += i[2]
        union(parents, i[0], i[1])
    if len(result) >= n - 1:
        break

print(result)
print(sum)

三、Prim算法

Prim算法（普里姆算法）是一种最小生成树算法，又称“加点法”，适合于稠密图中。

从图中的某个顶点开始，逐步扩大生成树的规模，直到包含所有顶点。在每一步中，选择连接生成树和图中其余部分的边中权重最小的边，将其添加到生成树中

注：最小生成树中具有n个节点，n-1条边。最小生成树不一定唯一，但最小生成树的边权值和唯一。

1. 算法步骤

初始化：选择图中的一个顶点作为起点，并将其加入生成树的集合S中。
标记未访问顶点：记录所有其他顶点到生成树S的最短距离。
选择最近顶点：在所有未访问的顶点中，找到距离生成树S最近的顶点v。
更新生成树：将顶点v添加到生成树S中，并更新所有未访问顶点的最短距离。
重复：重复步骤3和4，直到所有顶点都被添加到生成树S中。

2. 原理图解

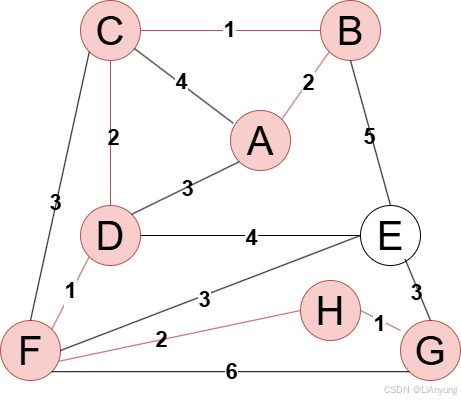
例如现在有一幅无向图，顶点为ABCDEFGH，边上数字表示边的权值。

Prim算法作为“加点法”，意为以“点”为核心，围绕“点”来进行记录。

为方便查询，也可以查看下列权值表：

	A	B	C	D	E	F	G	H
A		2	4	3
B			1		5
C				2		3
D					4	1
E						3	3
F							6	2
G								1
H

首先，随便选择一个点开始，这里我们选择A点演示。

将A节点加入生成树中，接下来继续选择距离生成树最近的节点，有B、C、D三个节点相接，其中B节点距离最近，距离仅为2，因此将B节点添加至生成树中。

上一轮选择结束得到如下图例。

A、B均已添加至生成树中，继续寻找距离生成树最近的点，有C、D、E三个节点相接，其中C节点距离最近，仅为1，因此将C节点添加至生成树中。

继续寻找距离生成树最近的节点，有D、E、F三个节点相接，其中D节点距离生成树最近，仅为2，因此，将D节点添加至生成树中。

继续添加节点，下一个添加节点F，最近距离为1。

下一步，在E、H、G三个节点中，H节点距离生成树最近，仅为2，因此将H节点添加至生成树中。

继续添加节点G，最近距离为1。

最后，E节点距离生成树最短距离为3，有EF和EG两条边，这种情况下，选择任意一条即可，符合最小生成树不唯一的特点。

得到最终的最小生成树，如下图所示：

树1

树2

上述两棵最小生成树均正确，符合最小生成树不唯一的特点，但最小生成树的权值和是唯一的，均为12。

3. 实现代码

基础代码，后续可使用堆进行优化。

def prim(graph):
    n = len(graph)
    # 创建处理后的图的副本，不修改原始数据
    processed_graph = [row[:] for row in graph]
    for i in range(n):
        for j in range(n):
            if i != j and processed_graph[i][j] == 0:
                processed_graph[i][j] = float('inf')

    dist = [processed_graph[0][j] for j in range(n)]  # 初始化距离为起始点邻接边
    visited = [False] * n
    visited[0] = True
    total_weight = 0

    for _ in range(n - 1):  # 需要选择n-1条边
        # 找到当前距离最小的未访问顶点
        min_dist = float('inf')
        u = -1
        for j in range(n):
            if not visited[j] and dist[j] < min_dist:
                min_dist = dist[j]
                u = j

        if u == -1:  # 图不连通，无法生成MST
            return -1

        total_weight += min_dist
        visited[u] = True

        # 仅更新新加入顶点的邻接边
        for v in range(n):
            if not visited[v] and processed_graph[u][v] < dist[v]:
                dist[v] = processed_graph[u][v]

    return total_weight


# 示例图（邻接矩阵）
graph = [
    [0, 2, 4, 3, 0, 0, 0, 0],
    [2, 0, 1, 0, 5, 0, 0, 0],
    [4, 1, 0, 2, 0, 3, 0, 0],
    [3, 0, 2, 0, 4, 1, 0, 0],
    [0, 5, 0, 4, 0, 3, 3, 0],
    [0, 0, 3, 1, 3, 0, 6, 2],
    [0, 0, 0, 0, 3, 6, 0, 1],
    [0, 0, 0, 0, 0, 2, 1, 0]
]

total = prim(graph)
print("总权重：", total)  # 正确输出应为 12

四、总结归纳

1. 相同点

最小生成树：两者的目标都是找到一个无向图的最小生成树，即一个连接所有顶点的生成树，使得树的边权之和最小。
贪心策略：Kruskal和Prim算法都采用了贪心算法的思想，每次选择当前情况下的最优解来逐步构建最小生成树。
适用范围：都适用于求解无向图的最小生成树问题，但对图的连通性有一定要求，Kruskal算法可以处理连通或非连通的图（通过生成森林），而Prim算法通常用于处理连通图。

2. 不同点

方面	Kruskal算法	Prim算法
贪心策略	每次选择全局最小的边，如果该边不形成环，就将其加入生成树。这种方法考虑全局最优。	从一个顶点开始，每次选择与生成树连接的最小权重边，逐步扩展生成树，每个步骤都考虑局部最优。
处理对象	Kruskal算法处理图的所有边，按权重从小到大排序，逐条考虑是否加入生成树。	Prim算法处理图的顶点，从一个顶点开始，逐步将顶点加入生成树，维护一个顶点集合，并不断更新与该集合相连的最小权重边。
适用场景	更适合稀疏图（边数较少的图），因为需要对所有边进行排序和并查集操作。	更适合稠密图（边数较多的图），因为Prim算法基于顶点的处理，不需要对所有边进行排序。
时间复杂度	O(E log E)，其中E是边的数量，主要用于对边进行排序，以及使用并查集操作来检测环。例如，使用Union-Find数据结构时，复杂度是可接受的。	基本实现为O(V²)，其中V是顶点的数量，但使用优先队列（如斐波那契堆）可以优化到O(E + V log V)。
空间需求	需要存储所有的边，并进行排序，空间需求与边数E相关。	需要存储顶点的最小距离和访问状态，空间需求与顶点数V相关。
问题处理	能够处理不连通的图，返回的是最小生成森林（每个连通分量的最小生成树）。	主要针对连通图，如果图不连通则无法生成整个图的最小生成树，但可以生成部分连通分量的树。