geodesic distance

1、python实现geodesic距离

其中见到的出现最多的名词之一就是 geodesic distance ，这个单词的中文翻译是测地距离，其实测地距离的意思就是在三维空间中，两点之间的最短路径，归根究底就是最短路径，在三维中间从一个点到另外一个点的路径有无数种，但是最短路径只有一条，那么这个最短路径的长度就是测地距离 geodesic distance。

# -*- coding: utf-8 -*-
"""
Created on Mon Jan 24 15:00:35 2022

@author: wmz
"""
import numpy as np
import matplotlib.pyplot as plt
import numpy.ma as ma

# %pylab
from scipy.ndimage.morphology import distance_transform_edt
l = 100
x, y = np.indices((l, l))
center1 = (50, 20)
center2 = (28, 24)
center3 = (30, 50)
center4 = (60,48)
radius1, radius2, radius3, radius4 = 15, 12, 19, 12
circle1 = (x - center1[0])**2 + (y - center1[1])**2 < radius1**2
circle2 = (x - center2[0])**2 + (y - center2[1])**2 < radius2**2
circle3 = (x - center3[0])**2 + (y - center3[1])**2 < radius3**2
circle4 = (x - center4[0])**2 + (y - center4[1])**2 < radius4**2
# 3 circles
img = circle1 + circle2 + circle3 + circle4
mask = ~img.astype(bool)
img = img.astype(float)
m = np.ones_like(img)
m[center1] = 0
#imshow(distance_transform_edt(m), interpolation='nearest')
m = ma.masked_array(distance_transform_edt(m), mask)
plt.imshow(m, interpolation='nearest')
plt.show()

I implemented the Dijkstra algorithm to apply a geodesic distance transform to the shape above:

# -*- coding: utf-8 -*-
"""
Created on Mon Jan 24 15:43:44 2022

@author: wmz
"""

import numpy
import numpy as np
import matplotlib.pyplot as plt
import numpy.ma as ma
from math import *
from numpy import *

# %pylab
from scipy.ndimage.morphology import distance_transform_edt


def geodesic_distance_transform(m):
    visit_mask = mask.copy() # mask visited cells
    m = m.filled(numpy.inf)
    m[m!=0] = numpy.inf
    distance_increments = numpy.asarray([sqrt(2), 1., sqrt(2), 1., 1., sqrt(2), 1., sqrt(2)])
    connectivity = [(i,j) for i in [-1, 0, 1] for j in [-1, 0, 1] if (not (i == j == 0))]
    cc = unravel_index(m.argmin(), m.shape) # current_cell
    while (~visit_mask).sum() > 0:
        neighbors = [tuple(e) for e in asarray(cc) - connectivity 
                     if not visit_mask[tuple(e)]]
        tentative_distance = [distance_increments[i] for i,e in enumerate(asarray(cc) - connectivity) 
                              if not visit_mask[tuple(e)]]
        for i,e in enumerate(neighbors):
            d = tentative_distance[i] + m[cc]
            if d < m[e]:
                m[e] = d
        visit_mask[cc] = True
        m_mask = ma.masked_array(m, visit_mask)
        cc = unravel_index(m_mask.argmin(), m.shape)
    return m


if __name__ == "__main__":
    
    l = 100
    x, y = np.indices((l, l))
    center1 = (50, 20)
    center2 = (28, 24)
    center3 = (30, 50)
    center4 = (60,48)
    radius1, radius2, radius3, radius4 = 15, 12, 19, 12
    circle1 = (x - center1[0])**2 + (y - center1[1])**2 < radius1**2
    circle2 = (x - center2[0])**2 + (y - center2[1])**2 < radius2**2
    circle3 = (x - center3[0])**2 + (y - center3[1])**2 < radius3**2
    circle4 = (x - center4[0])**2 + (y - center4[1])**2 < radius4**2
    # 3 circles
    img = circle1 + circle2 + circle3 + circle4
    mask = ~img.astype(bool)
    img = img.astype(float)
    m = np.ones_like(img)
    m[center1] = 0
    m = ma.masked_array(distance_transform_edt(m), mask)
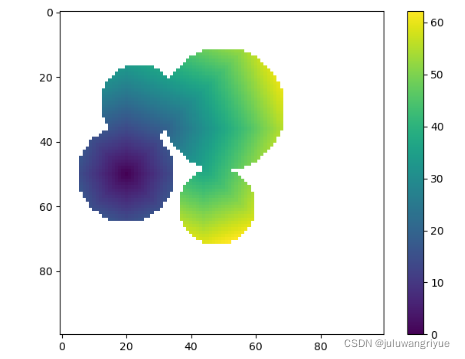
    gdt = geodesic_distance_transform(m)
    plt.imshow(gdt, interpolation='nearest')
    plt.colorbar()
    plt.show()

执行时间：

0.22861695289611816 s

安装软件包

conda install sscikit-fmm

# -*- coding: utf-8 -*-
"""
Created on Mon Jan 24 15:43:44 2022

@author: wmz
"""

import numpy
import numpy as np
import matplotlib.pyplot as plt
import numpy.ma as ma
from math import *
from numpy import *
import skfmm
import time
# %pylab
from scipy.ndimage.morphology import distance_transform_edt


def geodesic_distance_transform(m):
    visit_mask = mask.copy() # mask visited cells
    m = m.filled(numpy.inf)
    m[m!=0] = numpy.inf
    distance_increments = numpy.asarray([sqrt(2), 1., sqrt(2), 1., 1., sqrt(2), 1., sqrt(2)])
    connectivity = [(i,j) for i in [-1, 0, 1] for j in [-1, 0, 1] if (not (i == j == 0))]
    cc = unravel_index(m.argmin(), m.shape) # current_cell
    while (~visit_mask).sum() > 0:
        neighbors = [tuple(e) for e in asarray(cc) - connectivity 
                     if not visit_mask[tuple(e)]]
        tentative_distance = [distance_increments[i] for i,e in enumerate(asarray(cc) - connectivity) 
                              if not visit_mask[tuple(e)]]
        for i,e in enumerate(neighbors):
            d = tentative_distance[i] + m[cc]
            if d < m[e]:
                m[e] = d
        visit_mask[cc] = True
        m_mask = ma.masked_array(m, visit_mask)
        cc = unravel_index(m_mask.argmin(), m.shape)
    return m


if __name__ == "__main__":
    
    l = 100
    x, y = np.indices((l, l))
    center1 = (50, 20)
    center2 = (28, 24)
    center3 = (30, 50)
    center4 = (60,48)
    radius1, radius2, radius3, radius4 = 15, 12, 19, 12
    circle1 = (x - center1[0])**2 + (y - center1[1])**2 < radius1**2
    circle2 = (x - center2[0])**2 + (y - center2[1])**2 < radius2**2
    circle3 = (x - center3[0])**2 + (y - center3[1])**2 < radius3**2
    circle4 = (x - center4[0])**2 + (y - center4[1])**2 < radius4**2
    # 3 circles
    img = circle1 + circle2 + circle3 + circle4
    mask = ~img.astype(bool)
    img = img.astype(float)
    m = np.ones_like(img)
    m[center1] = 0
    m = ma.masked_array(m, mask) # distance_transform_edt(m)
    t1 = time.time()
    # gdt = geodesic_distance_transform(m)
    distance = skfmm.distance(m)
    t2 = time.time()
    eclipsed = t2 - t1
    print(eclipsed, "s")
    # plt.imshow(gdt, interpolation='nearest')
    plt.imshow(distance, interpolation='nearest')

    plt.colorbar()
    plt.show()

执行时间：

0.0009877681732177734 s

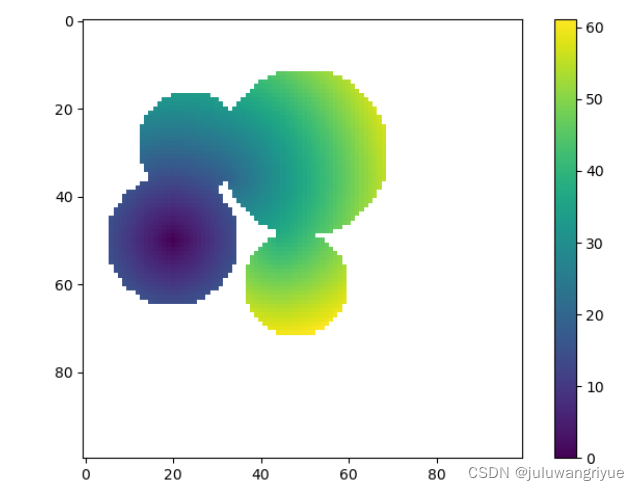
速度skfmm.distance是前者的231倍，效果skfmm.distance还要好于前者。

参考：关于 geodesic distance 的通俗解释
参考：geodesic distance transform in python

2、c++实现geodesic距离

编译与安装参考 GeographicLib 1.52

测试程序：
In order to use GeographicLib from C++ code, you will need to

Include the header files for the GeographicLib classes in your code. E.g.,

#include <GeographicLib/LambertConformalConic.hpp> 

Include the GeographicLib:: namespace prefix to the GeographicLib classes, or include

using namespace GeographicLib; 

in your code.

• Finally compile and link your code. You have two options here.
  • Use cmake to build your package. If you are familiar with cmake this typically will be far the simplest option.
  • Set the include paths and linking options “manually”.
• Building your code with cmake. In brief, the necessary steps are:

include in your CMakeLists.txt files

	find_package (GeographicLib REQUIRED)
    add_executable (program source1.cpp source2.cpp)
    target_link_libraries (program ${GeographicLib_LIBRARIES}) 

• configure your package, e.g., with

 mkdir BUILD
    cd BUILD
    cmake -G "Visual Studio 14" -A x64 \
      -D CMAKE_PREFIX_PATH="C:/Program Files" \
      -D CMAKE_INSTALL_PREFIX="C:/Program Files/testgeog" \
      .. 

Here is a very simple test code, which uses the Geodesic class:

// Small example of using the GeographicLib::Geodesic class
 
#include <iostream>
#include <GeographicLib/Geodesic.hpp>
 
using namespace std;
using namespace GeographicLib;
 
int main() {
  const Geodesic& geod = Geodesic::WGS84();
  // Distance from JFK to LHR
  double
    lat1 = 40.6, lon1 = -73.8, // JFK Airport
    lat2 = 51.6, lon2 = -0.5;  // LHR Airport
  double s12;
  geod.Inverse(lat1, lon1, lat2, lon2, s12);
  cout << s12 / 1000 << " km\n";
}

完整CMakeLists.txt

project (geodesictest)
cmake_minimum_required (VERSION 3.1.0)

find_package (GeographicLib REQUIRED)

if (NOT MSVC)
  set (CMAKE_INSTALL_RPATH_USE_LINK_PATH TRUE)
endif ()

add_executable (${PROJECT_NAME} example-Geodesic-small.cpp)
target_link_libraries (${PROJECT_NAME} ${GeographicLib_LIBRARIES})

if (MSVC)
  get_target_property (_LIBTYPE ${GeographicLib_LIBRARIES} TYPE)
  if (_LIBTYPE STREQUAL "SHARED_LIBRARY")
    # On Windows systems, copy the shared library to build directory
    add_custom_command (TARGET ${PROJECT_NAME} POST_BUILD
      COMMAND ${CMAKE_COMMAND} -E
      copy $<TARGET_FILE:${GeographicLib_LIBRARIES}> ${CMAKE_CFG_INTDIR}
      COMMENT "Copying shared library for GeographicLib")
  endif ()
endif () 

参考：C library for Geodesics 1.52
参考：GeographicLib 1.52
参考：