遗传算法的matlab实现

遗传算法的matlab实现

遗传算法是仿照达尔文生物进化的原理来实现的智能搜索技术。主要原理如下：对于一个种群，这个种群中有一定数量的个体，而每个个体对这个种群所在的环境的适应性各不相同，适应性强的个体便能有更强的存活几率，那么随着种群一代一代的进化，适应性强的个体的基因在后代种群中所占的比例就会越来越大，只要环境基本保持不变，整个种群对于环境的适应性变回越来越强。
根据这个原理所发明的智能搜索技术其实可以描述为这样一个场景：假如我们有一个函数：

f(x,y,z) = x^2+3*sin(x*y*z)+y^2-z^2

要找到这个函数在

1. x~(-10,10)
2. y~(-10,10)
3. z~(-10,10)

的范围内这个函数的最小值或者最大值所对应的点，我们使用遗传算法来求解这个最大值或者最小值，那么思路就是，首先，我们构造一个种群，假设这个种群中有两百个个体，每个个体为在坐标范围x（-10,10）y（-10,10），z（-10,10）内部的一个点，而我们的目的就是寻找到函数的最大值或者最小值，所以每个个体对于环境的适应性可以表述为由每个个体所对应于给定空间中的点的坐标（x0,y0,z0），代入函数f(x,y,z) = x^2-3*sin(x*y*z)+y^2-z^2后所求解得到的函数值，假设我们需要求解最大值，那么如果一个个体所求解出的函数值越大，我们就认为这个个体越符合我们的要求，那么这个个体对于环境的适应性就越强。之后，我们再采用仿照生物进化的手段让种群发生进化，最终得到近似全局最优解。
综上，我们可以用一个向量[x0,y0,z0]来表示一个个体,那么一个种群就是个体的集合，也就是一个矩阵，一个有200个个体的种群便是由200个3x1的列向量组成的3x200的矩阵，那么如何来构造一个种群呢？我们来想象一下草原上的一个牛群，牛群中的牛有的强壮，有的瘦弱，有的是小牛，有的是老牛，这些抽象来说就是牛群中的牛对于这个环境的适应性不同，年轻力壮的牛自然能获得更多的食物更多的繁衍后代的机会，在遇到天敌是有更多的生存几率，老弱病残的牛自然生存的几率就小的多，所以我们要构造一个这样的种群，这个种群有年轻力壮的个体，也有老弱病残的个体，而我们之前构造的个体其实就是空间中的一个坐标点，位于不同空间中的坐标所对应的函数值也不同，所以构造一个种群就是让这个种群中的个体尽量均匀的分布于这个空间当中，其实就是构造200个列向量，每个列向量都是空间中的随机的一个点，我们可以有matlab中的rands函数来构造，如下：

>> rands(3,200)*10

ans = 
5.0679   -3.7459    3.8999    7.9501  … -6.6495
9.5379   -2.4900   -5.3818   -8.6817  … 4.0117
2.5413   -3.0310    1.1492    3.0234  … -8.7508

好了，到目前为止，已经构造好了一个种群了，接下来我们让这个种群发生变异。
牛群当中的变异主要是由公牛和母牛交配繁殖后代以及后代的基因发生的自然变异，也就是说后代的基因一部分由公牛和母牛的基因组成，另一部分由变异组成。简化来说就是两种：1，父代的染色体的交叉2，后代染色体的自我变异。现在来用向量实现上面两种进化：1，染色体的交叉，由于我们的父代的都是由向量组成的，我们可以把向量当做成染色体，两个染色体的交叉，其实就对应于两个父代向量之间交换向量片段。2，后代染色体的自我变异，其实就是后代个体的3x1的列向量中的某一个元素的值随机的发生了变化。到这里我们已经完成了种群的变异操作，但是一个种群光有变异还不行，假如有一个强壮的牛群，这个牛群中的强壮的牛的数量一定是比一个普通的牛群中强壮的牛的数量要大，也就是说我们要让我们的种群中的适应性强的个体变得越来越多，那么我们要做的就是，把种群中适应性差的个体剔除掉，适应性强的个体保留下来，这样构成的新的种群中适应性强的个体相对来说就比之前的种群要多，然后种群没变异一次我们就这样做一次，最终整个种群中的个体的适应性都达到了较高的水平，我们从这些优质个体中选择出适应性最强的个体，这个个体多代表的空间坐标便就是我们所求的函数的最大值所对应的点了。但是由于进化的过程中引入了随机操作所以每次进化的得到的最终的种群的最优解有一定小幅度的波动。

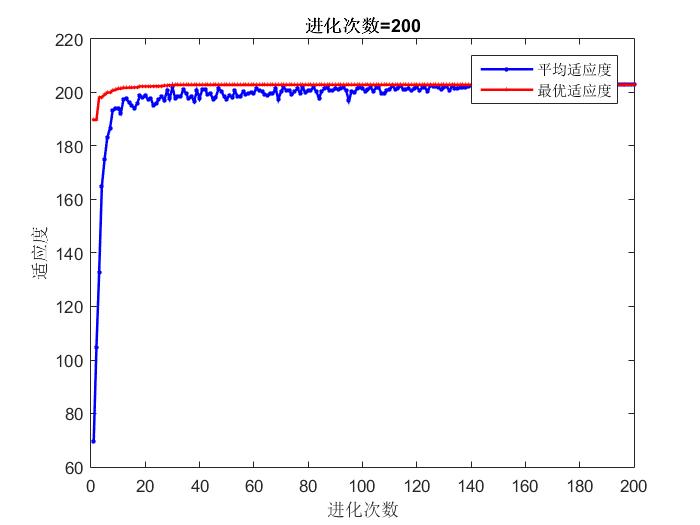
下面我们看一个具体的实例，求解函数f(x,y,z) = x^2+3*sin(x*y*z)+y^2-z^2在x~(-10,10),y~(-10,10),z~(-10,10)的范围内的最大值所对应的点的坐标，按照上面的算法，我们利用matlab求解，得到最优解如下：

迭代得到的适应度值随着进化代数图如下