粒子群算法的matlab实现

粒子群算法，也称粒子群优化算法（Particle Swarm Optimization），缩写为 PSO， 是近年来发展起来的一种新的进化算法(Evolutionary Algorithm - EA)。PSO 算法属于进化算法的一种，和模拟退火算法相似，它也是从随机解出发，通过迭代寻找最优解，它也是通过适应度来评价解的品质，但它比遗传算法规则更为简单，它没有遗传算法的“交叉”(Crossover) 和“变异”(Mutation) 操作，它通过追随当前搜索到的最优值来寻找全局最优。这种算法以其实现容易、精度高、收敛快等优点引起了学术界的重视，并且在解决实际问题中展示了其优越性。粒子群算法是一种并行算法。

---

下面具体介绍粒子群算法的matlab实现：
目标函数：f = x1**2+x2**2-x3**2+3*sin(x1*x2*x3)
求解：在坐标范围x~(-10,10) z~(-10,10) y~(-10,10)的范围中的最大值，以及最大值所对应的x1,x2,x3

算法步骤：

---

首先初始化参数

%参数初始化
c1=1.49445;c2=1.49445;
maxgen=200; % 最大进化次数                                                      
sizepop=100; %粒子总数                                                        
psize = 3; % 粒子大小
Vmax=5;Vmin=-5; % 粒子移动速度范围                                           
lb = ones(psize,1)*(-10);
ub = ones(psize,1)*10;
bound = [lb,ub]; % 粒子移动的范围
wstart = 0.9;wend = 0.4; % 惯性权重

其中，惯性权重用来调节算法的寻优能力，当权重较大时，算法有较强的全局寻优能力，当权重较小时，算法有较强的局部寻优能力，在算法的运行当中，调节权重由大到小的变化，提升算法的性能。

---

惯性权重调节公式：

w = wstart-(wstart-wend)*((i1/maxgen)^2);

---

粒子群初始化，初始化粒子群中各个粒子的速度和位置

%产生初始粒子位置和速度
pop=zeros(sizepop,psize);
V=zeros(sizepop,psize);
fitness=zeros(1,sizepop);
for i1=1:sizepop
    %随机产生一个种群
    pop(i1,:) = (bound(:,2)-bound(:,1))'.*rand(1,psize)+bound(:,1)';
    V(i1,:)=rands(1,psize)*(Vmax-Vmin)+Vmin;                                        %随机初始化粒子速度
    %计算适应度
    fitness(i1)=fun(pop(i1,:));
end

粒子速度更新

V(i2,:)=w*V(i2,:)+c1*rand*(gbest(i2,:) - pop(i2,:))+c2*rand*(zbest - pop(i2,:));

限制粒子的速度上下限

tempV = V(i2,:);
tempV(tempV > Vmax) = Vmax;
tempV(tempV < Vmin) = Vmin;
V(i2,:) = tempV;

粒子位置更新

pop(i2,:)=pop(i2,:)+V(i2,:);

限制粒子位置的上下限

% 粒子位置限制
        for i3 = 1:psize
            if pop(i2,i3) >= bound(i3,2)
                pop(i2,i3) = bound(i3,2);
            end
            if pop(i2,i3) <= bound(i3,1)
                pop(i2,i3) = bound(i3,1);
            end
        end

---

算法运行结果

---

---

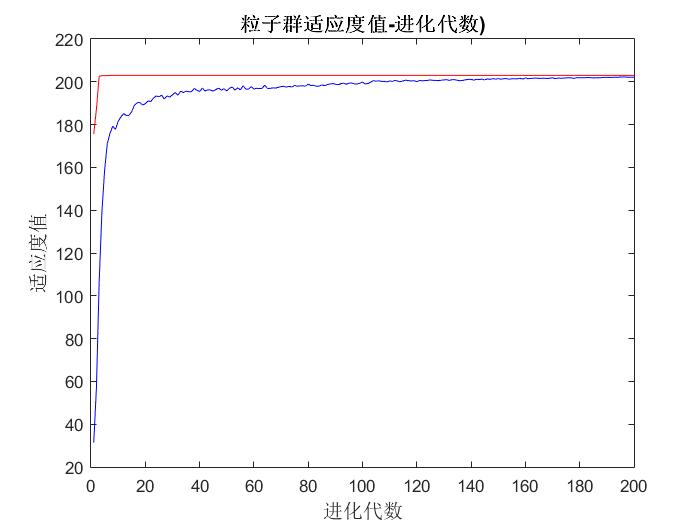
平均适应度值和最优适应度值随着进化代数变化

对比之前用python实现的粒子群算法，python用了1.2秒左右，matlab却只用了0.6秒左右，而之前对比了python和matlab实现的遗传算法，python又比matlab要快，看来语言的快慢有时候并不是算法性能的绝对因素，算法的具体实现技巧也很关键！