梯度下降法求解线性回归之matlab实现

线性回归其实就是寻找一条直线拟合数据点，使得损失函数最小。直线的表达式为：

$$y_i = \omega_1x_{i,1}+\omega_2x_{i,2}+\omega_jx_{i,j}+...+b$$
损失函数的表达式为：
$$J = \frac{1}{2}\sum_{i=0}^m{(y_i-y_{predict\_i})^2}$$
其中m为数据点总数。
现在我们使用梯度下降法求解函数$J$的最小值，梯度下降法原理示意图如下：

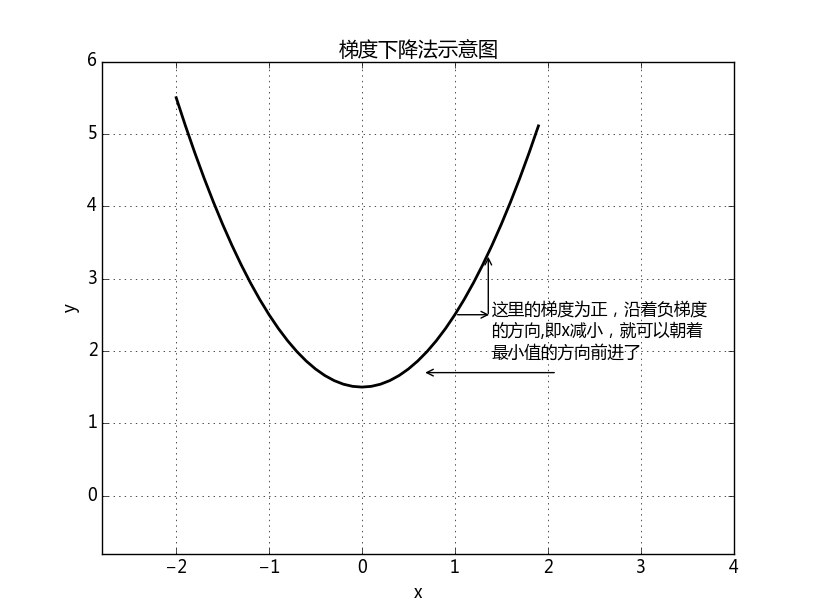
如上图所示，只要自变量$x$沿着负梯度的方向变化，就可以到达函数的最小值了，反之，如果沿着正梯度方向变化，就可以到达函数的最大值。
我们要求解$J$函数的最小值，那么就要求出每个$\omega$的梯度和$b$的梯度，由于梯度太大，可能会导致自变量沿着负梯度方向变化时，$J$的值出现震荡，而不是一直变小，所以在梯度的前面乘上一个很小的系数$\alpha$。
由以上可以总结出$\omega$和$b$的更新公式：

$$\omega_j = \omega_j-\alpha\nabla{J}(\omega_j)$$
$$b = b-\alpha\nabla{J}(b)$$
梯度公式（其实就是求导而已）：
$$\begin{align} \nabla{J}(\omega_j) & = \frac{\partial{J}}{\partial{\omega_j}} \\ & = \sum_{i=0}^m{(y_i-y_{predict\_i})(-x_{i,j})}\\ & = \sum_{i=0}^m{(y_{predict\_i}-y_i)x_{i,j}}\\ \end{align}$$
$$\begin{align} \nabla{J}(b) & = \frac{\partial{J}}{\partial{b}} \\ & = \sum_{i=0}^m{(y_{predict\_i}-y_i)}\\ \end{align}$$
系数$\alpha$如果随着迭代的进行越来越小的话，有利于防止迭代后期震荡的发生，是算法收敛，$\alpha$的更新公式：
$$\alpha = \frac{1}{i+1}+0.001$$
其中i是迭代次数，起始为0
下面是matlab的具体实现

---

样例数据

x = linspace(-2,2,40)';
y = 2*x+rand(length(x),1);

开始迭代

for i = 1:maxgen
    alpha = 1/i+alpha0;
    e = x*seta+b-y;
    mse = norm(e);
    delta_seta = e'*x;
    delta_seta_norm = norm(delta_seta);
    b = b-alpha*sum(e);
    seta = seta-alpha*delta_seta;
    disp(strcat('迭代次数:',num2str(i)));
    disp(strcat('梯度：',num2str(delta_seta_norm),';seta:',num2str(seta),';b:',num2str(b),';mse:',num2str(mse)))
    disp(strcat('alpha:',num2str(alpha),';sum(e):',num2str(sum(e))))

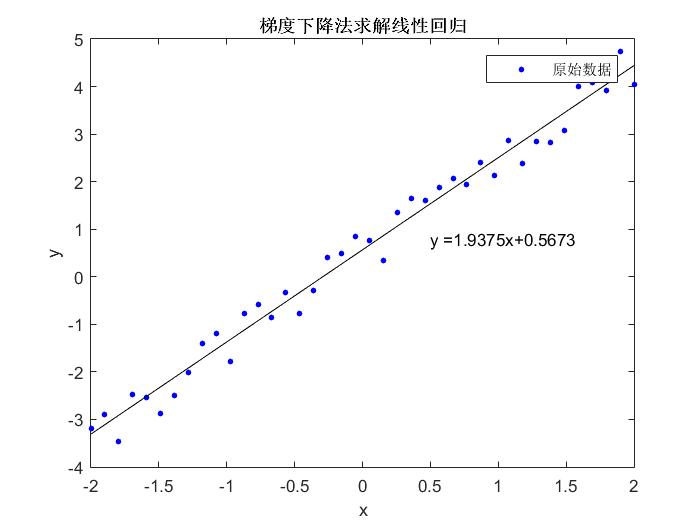
end

程序运行结果：

---