概述
树上差分有什么作用?举个例子,如果题目要求对树上的一段路径进行操作,并询问某个点或某条边被经过的次数,树上差分就可以派上用场了。这就是树上差分的基本操作。
树上差分,就是利用差分的性质,对路径上的重要节点进行修改(而不是暴力全改),作为其差分数组的值,最后在求值时,利用 dfs 遍历求出差分数组的前缀和,就可以达到降低复杂度的目的。树上差分时需要求 LCA(Least Common Ancestors,最近公共祖先)。
树上差分思想和一维二维差分一样,只不过最后做和的时候不同。树上差分的做和 C[i] = C[i]+(其子树的所有节点的C),也就用dfs再跑一次树 求和。还有一点值得注意的就是,对点和边的树上差分原理相同,实现略有不同点权差分和边权差分有些许不同。
在讲树上差分之前,首先需要知道树的以下两个性质:
(1)任意两个节点之间有且只有一条路径。
(2)根节点确定时,一个节点只有一个父亲节点。
这两个性质都很容易证明。那么我们知道,如果假设我们要考虑的是从 u 到 v 的路径,u 与 v 的 LCA 是 a。那么很明显,如果路径中有一点 u′ 已经被访问了,且 u′≠a,那么 u' 的父亲也一定会被访问,这是根据以上性质可以推出的。所以,我们可以将路径拆分成两条链,u->a 和 a->v。
点的差分
我们从 s−−>t 求这条路径上的点被经过的次数。如下图所示,绿色的数字表示经过的次数。很明显的,我们需要找到他们的 LCA,因为这个点 LCA 是中转点啊。我们需要让 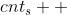 ,让
,让 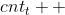 ,而让他们的
,而让他们的 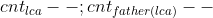 。
。

根据上面的思路,我们的标记应该是如下图所示。

以 u 表示当前结点,son代表当前结点 u 的儿子,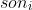 代表结点 i 的儿子结点。
代表结点 i 的儿子结点。
1、我们从跟结点出发搜索到 s,然后向上回溯。
2、每个 u 统计它的子树大小,顺着路径标起来,即 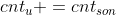 。回发现第一次从 s 回溯到他们的 LCA 时候,
。回发现第一次从 s 回溯到他们的 LCA 时候,![cnt_{LCA} += cnt[son_{LCA}]](https://i-blog.csdnimg.cn/blog_migrate/d3634688d5824392a273ed074e529083.gif) ,且
,且 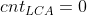 。
。
3、搜索到 t 向上回溯,依旧统计每个 u 的子树大小 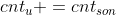 ,这样再度会到 LCA 依旧是
,这样再度会到 LCA 依旧是 ![cnt_{LCA} += cnt[son_{LCA}]](https://i-blog.csdnimg.cn/blog_migrate/d3634688d5824392a273ed074e529083.gif) ,这个时候
,这个时候 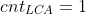 ,这样就达到了我们要的效果(每个结点就访问一次)。
,这样就达到了我们要的效果(每个结点就访问一次)。
4、万一我们再从 LCA 向上回溯的时候使得其父亲节点的子树和为 1 怎么办?这样我们不就使得其父亲节点被经过了一次?因此我们需要在 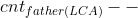 ,这样就达到了标记我们路径上的点的要求。
,这样就达到了标记我们路径上的点的要求。
思路
对于所要求的路径,拆分成两条链。关于点,u 与 v 的 LCA 是需要包括进去的,所以要把 LCA 包括在某一条链中,用 cf[i] 表示 i 被访问的次数。最后对 cf 数组的操作便是 cf[u]++,cf[v]++,cf[a]−−,cf[father[a]]−−。其时间复杂度也是一样的 Θ(n)。
图例
设将两点 u,v 之间路径上的所有点权增加 x,o=LCA(u,v),o 的父亲节点为 p,则操作如下:
diff[u]+=x;
diff[v]+=x;
diff[o]-=x;
diff[p]-=x;下面我们用一个例子来说明。设原树如下图,现要将 2,3 之间路径上的所有点的权值增加 3,设原权值均为 0。
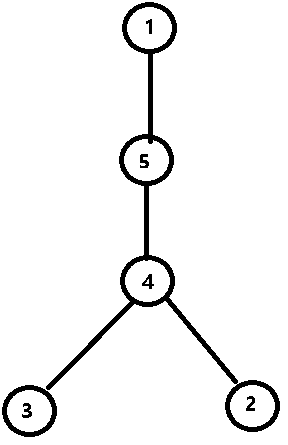
则操作后的树如下图所示。

这样,只要 dfs 一遍,遍历时统计以每个节点为根的树的节点的权值和,就是当前节点的最终权值!
边的差分
如找被所有路径共同覆盖的边。
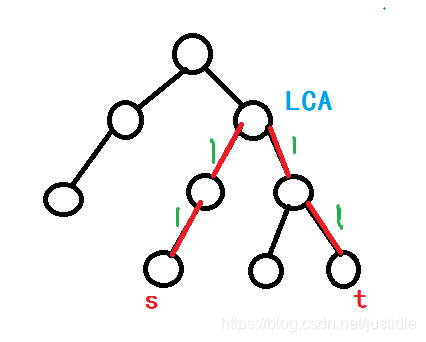
我们对边进行差分需要把边塞给点,但是,这里的标记并不是同点差分一样。把边塞给点的话,是塞给这条边所连的深度较深的节点(即塞给儿子节点)。我们从 s−−>t 求边的差分,正常的话我们的图是如下图所示,红色边为需要经过的边,绿色的数字代表经过次数。
但是由于我们把边塞给了点,因此我们的图应该是如下图所示。

但是根据我们点差分的标记方式来看的话显然是行不通的,因为我们会经过 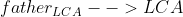 这一路径。这样我们可以这样来标记:
这一路径。这样我们可以这样来标记:

这样回溯的话,我们即可只经过图中红色边。把边塞入点中的代码这样写:
void dfs(int u,int fa,int dis) {
//u为当前节点,fa为当前节点的父亲节点,dis为从fa通向u的边的边权.
depth[u]=depth[fa]+1;
f[u][0]=fa;//相信写过倍增LCA的人都能看懂.
init[u]=dis;//这里是将边权赋给点.
for(int i=1; (1<<i)<=depth[u]; i++) {
f[u][i]=f[f[u][i-1]][i-1];//预处理倍增数组.
}
for(int i=head[u]; i; i=edge[i].u) {
if (edge[i].v==fa) {
continue;
}
dfs(edge[i].v, u, edge[i].w);
}
}思想
将边拆成两条链之后,我们便可以像差分一样来找到路径了。用 cf[i] 代表从 i 到 i 的父亲这一条路径经过的次数。因为关于边的差分,a 是不在其中的,所以考虑链 u->a,则就要使 cf[u]++,cf[a]−−。然后链 a->v,也是 cf[v]++,cf[a]−−。所以合起来便是 cf[u]++,cf[v]++,cf[a]−=2。然后,从根节点,对于每一个节点 x,都有如下的步骤:
(1)枚举 x 的所有子节点 u;
(2)dfs 所有子节点 u;
(3)cf[x]+=cf[u]。
那么,为什么能够保证这样所有的边都能够遍历到呢?因为我们刚刚已经说了,如果路径中有一点 u′ 已经被访问了,且 u′≠a,那么 u′ 的父亲也一定会被访问。所以 u′ 被访问几次,它的父亲也就因为 u′ 被访问了几次。所以就能够找出所有被访问的边与访问的次数了。路径求交等一系列问题就是通过这个来解决的。因为每个点都只会遍历一次,所以其时间复杂度为 Θ(n)。
图例
设将两点 u,v 之间路径上的所有边权增加 x,o=LCA(u,v),以每条边两端深度较大的节点存储该边的差分数组,则操作如下:
diff[u]+=x;
diff[v]+=x;
diff[o]-=2*x;下面我们用一个例子来说明。设原树如下图,现要将 2,3 之间路径上的所有点的权值增加 3,设原权值均为 0。

则操作后的树如下图所示。

这样,只要 dfs 一遍,遍历时统计以每个节点为根的树的节点的权值和,就是当前节点的最终权值!
习题
模板题
洛谷的 P1083,https://www.luogu.com.cn/problem/P3128。
参考资料
差分数组 and 树上差分,https://www.luogu.com.cn/blog/RPdreamer/ci-fen-and-shu-shang-ci-fen。




























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










