T1:
题目描述:
P老师需要去商店买n支铅笔作为小朋友们参加NOIP的礼物。她发现商店一共有 3种包装的铅笔,不同包装内的铅笔数量有可能不同,价格也有可能不同。为了公平起 见,P老师决定只买同一种包装的铅笔。商店不允许将铅笔的包装拆开,因此P老师可能需要购买超过n支铅笔才够给小朋 友们发礼物。现在P老师想知道,在商店每种包装的数量都足够的情况下,要买够至少n支铅笔最少需要花费多少钱。
输入格式:
输入的第一行包含一个正整数n,表示需要的铅笔数量。接下来三行,每行用两个正整数描述一种包装的铅笔:其中第一个整数表示这种 包装内铅笔的数量,第二个整数表示这种包装的价格。保证所有的7个数都是不超过10000的正整数。
输出格式:
输出一行一个整数,表示P老师最少需要花费的钱。
输入样例1:
57
2 2
50 30
30 27
输出样例1:
54
输入样例2:
9998
128 233
128 2333
128 666
输出样例2:
18407
输入样例3:
9999
101 1111
1 9999
1111 9999
输出样例3:
89991
说明
铅笔的三种包装分别是:
•2支装,价格为2; •50支装,价格为30; •30支装,价格为27。
P老师需要购买至少57支铅笔。如果她选择购买第一种包装,那么她需要购买29份,共计2x29 = 58支,需要花 费的钱为2x29 = 58。实际上,P老师会选择购买第三种包装,这样需要买2份。虽然最后买到的铅笔数 量更多了,为30x2 = 60支,但花费却减少为27 x2 = 54,比第一种少。对于第二种包装,虽然每支铅笔的价格是最低的,但要够发必须买2份,实际的 花费达到了 30 x 2 = 60,因此P老师也不会选择。所以最后输出的答案是54。
题解:
枚举每个包装,判断一下n是不是当前这个包装数量的整倍数,
如果是的话就直接用n/包装数量*每个的价钱,
如果不是的话,就用(n/包装数量+1)*每个的价钱,最后再判断最小值就好了
参考代码:
var n,x1,y1,x2,y2,x3,y3,min1,min2,min3:longint;
function min(x,y:longint):longint;
begin
if x<y then exit(x) else exit(y);
end;
begin
assign(input,'pencil.in');reset(input);
assign(output,'pencil.out');rewrite(output);
readln(n);
readln(x1,y1);
readln(x2,y2);
readln(x3,y3);
if n mod x1>0 then min1:=(n div x1+1)*y1 else min1:=(n div x1)*y1;
if n mod x2>0 then min2:=(n div x2+1)*y2 else min2:=(n div x2)*y2;
if n mod x3>0 then min3:=(n div x3+1)*y3 else min3:=(n div x3)*y3;
writeln(min(min(min1,min2),min3));
close(input);close(output);
end.
T2:
题目描述:
在日常生活中,通过年、月、日这三个要素可以表示出一个唯一确定的日期。
牛牛习惯用8位数字表示一个日期,其中,前4位代表年份,接下来2位代表月 份,最后2位代表日期。显然:一个日期只有一种表示方法,而两个不同的日期的表 示方法不会相同。牛牛认为,一个日期是回文的,当且仅当表示这个日期的8位数字是回文的。现 在,牛牛想知道:在他指定的两个日期之间包含这两个日期本身),有多少个真实存 在的日期是回文的。一个8位数字是回文的,当且仅当对于所有的i ( 1 <=i<= 8 )从左向右数的第i个 数字和第9-i个数字(即从右向左数的第i个数字)是相同的。
例如:•对于2016年11月19日,用8位数字20161119表示,它不是回文的。 •对于2010年1月2日,用8位数字20100102表示,它是回文的。 •对于2010年10月2日,用8位数字20101002表示,它不是回文的。
每一年中都有12个月份:其中,1、3、5、7、8、10、12月每个月有31天;4、6、9、11月每个月有30天;而对于2月,闰年时有29天,平年时有28天。
一个年份是闰年当且仅当它满足下列两种情况其中的一种:1.这个年份是4的整数倍,但不是100的整数倍;2.这个年份是400的整数倍。
例如:•以下几个年份都是闰年:2000、2012、2016。 •以下几个年份是平年:1900、2011、2014。
输入格式:
输入包括两行,每行包括一个8位数字。第一行表示牛牛指定的起始日期。第二行表示牛牛指定的终止日期。保证date_i和都是真实存在的日期,且年份部分一定为4位数字,且首位数字不为0。保证date1 —定不晚于date2。
输出格式:
输出一行,包含一个整数,表示在date1和date2之间,有多少个日期是回文的。
输入样例1:
20110101
20111231
输出样例1:
1
输入样例2:
20000101
20101231
输出样例2:
2
【样例说明】
对于样例1,符合条件的日期是20111102。对于样例2,符合条件的日期是20011002和20100102。
【子任务】对于60%的数据,满足date1 = date2。
题解:
这道题可以直接一天一天枚举,不会超时,
注意判断闰年平年时二月日期
参考代码:
var a:array[1..12]of longint=(31,28,31,30,31,30,31,31,30,31,30,31);
s1,s2,s3:string;
i,j,bz,x1,x2,x3,y1,y2,y3,tot:longint;
begin
assign(input,'date.in');reset(input);
assign(output,'date.out');rewrite(output);
readln(s1);
readln(s2);
val(copy(s1,1,4),x1);
val(copy(s1,5,2),x2);
val(copy(s1,7,2),x3);
val(copy(s2,1,4),y1);
val(copy(s2,5,2),y2);
val(copy(s2,7,2),y3);
for i:=1to 4 do
if s1[i]<>s1[9-i] then
begin
bz:=1;
break;
end;
if bz=0 then inc(tot);
while(x1<y1)or((x1=y1)and(x2<y2))or((x1=y1)and(x2=y2)and(x3<y3)) do
begin
inc(x3);
if x3>a[x2] then
begin
if (x2=2)and(x3=29)and(((x1 mod 4=0)and(x1 mod 100>0))or(x1 mod 400=0)) then else
begin
x3:=1;
inc(x2);
if x2>12then
begin
x2:=1;
inc(x1);
end;
end;
end;
str(x1,s1);
str(x2,s2);
str(x3,s3);
if x2>9 then s1:=s1+s2 else s1:=s1+'0'+s2;
if x3>9 then s1:=s1+s3 else s1:=s1+'0'+s3;
bz:=0;
for i:=1 to 4 do
if s1[i]<>s1[9-i] then
begin
bz:=1;
break;
end;
if bz=0 then inc(tot);
end;
writeln(tot);
close(input);close(output);
end.
T3:
题目描述:
小K是一个海港的海关工作人员,每天都有许多船只到达海港,船上通常有很多来自不同国家的乘客。小K对这些到达海港的船只非常感兴趣,他按照时间记录下了到达海港的每一艘船只情况;对于第i艘到达的船,他记录了这艘船到达的时间ti (单位:秒),船上的乘 客数星ki,以及每名乘客的国籍 x(i,1), x(i,2),…,x(i,k);。小K统计了n艘船的信息,希望你帮忙计算出以每一艘船到达时间为止的24小时(24小时=86400秒)内所有乘船到达的乘客来自多少个不同的国家。形式化地讲,你需要计算n条信息。对于输出的第i条信息,你需要统计满足 ti - 86400 < tp <= ti的船只p,在所有的x(p,j)中,总共有多少个不同的数。
输入格式:第一行输入一个正整数n,表示小K统计了 n艘船的信息。接下来n行,每行描述一艘船的信息:前两个整数ti和ki分别表示这艘船到达海港的时间和船上的乘客数量,接下来ki个整数x(i,j)表示船上乘客的国7。保证输入的ti是递增的,单位是秒;表示从小K第一次上班开始计时,这艘船在第 ti 秒到达海港。
保证 ,
,
,
。其中
表示所有的ki的和。
输出格式:输出n行,第i行输出一个整数表示第i艘船到达后的统计信息。
输入样例1:
3
1 4 4 1 2 2
2 2 2 3
10 1 3
输出样例1:
3
4
4
输入样例2:
4
1 4 1 2 2 3
3 2 2 3
86401 2 3 4
86402 1 5
输出样例2:
3
3
3
4
【样例解释1】第一艘船在第1秒到达海港,最近24小时到达的船是第一艘船,共有4个乘客, 分别是来自国家4,1,2,2,共来自3个不同的国家;第二艘船在第2秒到达海港,最近24小时到达的船是第一艘船和第二艘船,共有 4 + 2 = 6个乘客,分别是来自国家4,1,2,2,2,3,共来自4个不同的国家;第三艘船在第10秒到达海港,最近24小时到达的船是第一艘船、第二艘船和第 三艘船,共有4+ 2+1=7个乘客,分别是来自国家4,1,2,2,2,3,3,共来自4个不同 的国家。
【样例解释2】第一艘船在第1秒到达海港,最近24小时到达的船是第一艘船,共有4个乘客,分别是来自国家1,2,2,3,共来自3个不同的国家。第二艘船在第3秒到达海港,最近24小时到达的船是第一艘船和第二艘船,共有4+2=6个乘客,分别是来自国家1,2,2,3,2,3,共来自3个不同的国家。第三艘船在第86401秒到达海港,最近24小时到达的船是第二艘船和第三艘船,共有2+2=4个乘客,分别是来自国家2,3,3,4,共来自3个不同的国家。第四艘船在第86402秒到达海港,最近24小时到达的船是第二艘船、第三艘船和第四艘船,共有2+2+1=5个乘客,分别是来自国家2,3,3,4,5,共来自4个不同的国家。
题解:
简单来讲就是每次输入直接把船上游客拆开用队列记录时间和国家,
然后如果存入时发现这个国家编号都不与其它在队列中的国家编号相同,
ans+1并记录国家编号出现次数;
然后每次从当前队首枚举过来,
如果发现时间在一天外就删去,
且如果删去的国家编号是都不与其它在队列中国家编号相同,则ans-1
每次输入后输出ans就可以了
参考代码:
var a:array[1..300000,1..2]of longint;
b:array[1..100000]of longint;
i,k,m,n,ans,l,r,t:longint;
begin
assign(input,'port.in');reset(input);
assign(output,'port.out');rewrite(output);
readln(m);
r:=1;
for k:=1 to m do
begin
read(t,n);
for i:=1 to n do
begin
inc(l);
read(a[l,1]);
if b[a[l,1]]=0 then inc(ans);
inc(b[a[l,1]]);
a[l,2]:=t;
end;
while t-a[r,2]>86399 do
begin
dec(b[a[r,1]]);
if b[a[r,1]]=0 then dec(ans);
inc(r);
end;
writeln(ans);
end;
close(input);close(output);
end.
T4:
题目描述:
六十年一次的魔法战争就要开始了,大魔法师准备从附近的魔法场中汲取魔法能量。大魔法师有m个魔法物品,编号分别为1,2,...,m。每个物品具有一个魔法值,我们用Xi表示编号为i的物品的魔法值。每个魔法值Xi是不超过n的正整数,可能有多个物品的魔法值相同。大魔法师认为,当且仅当四个编号为a,b,c,d的魔法物品满足xa<xb<xc<xd,Xb-Xa=2(Xd-Xc),并且xb-xa<(xc-xb)/3时,这四个魔法物品形成了一个魔法阵,他称这四个魔法物品分别为这个魔法阵的A物品,B物品,C物品,D物品。现在,大魔法师想要知道,对于每个魔法物品,作为某个魔法阵的A物品出现的次数,作为B物品的次数,作为C物品的次数,和作为D物品的次数。
输入格式:输入文件的第一行包含两个空格隔开的正整数n和m。接下来m行,每行一个正整数,第i+1行的正整数表示Xi,即编号为i的物品的魔法值。保证,
,
。每个Xi是分别在合法范围内等概率随机生成的。
输出格式:共输出m行,每行四个整数。第i行的四个整数依次表示编号为i的物品作 为A,B,C,D物品分别出现的次数。
保证标准输出中的每个数都不会超过10^9。
每行相邻的两个数之间用恰好一个空格隔开。
输入样例1:
30 8
1
24
7
28
5
29
26
24
输出样例1:
4 0 0 0
0 0 1 0
0 2 0 0
0 0 1 1
1 3 0 0
0 0 0 2
0 0 2 2
0 0 1 0
输入样例2:
15 15
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
输出样例2:
5 0 0 0
4 0 0 0
3 5 0 0
2 4 0 0
1 3 0 0
0 2 0 0
0 1 0 0
0 0 0 0
0 0 0 0
0 0 1 0
0 0 2 1
0 0 3 2
0 0 4 3
0 0 5 4
0 0 0 5
【样例解释1】共有5个魔法阵,分别为:物品1,3,7,6,其魔法值分别为1,7,26,29;物品1,5,2,7,其魔法值分别为1,5,24,26;物品1,5,7,4,其魔法值分别为1,5,26,28;物品1,5,8,7,其魔法值分别为1,5,24,26;物品5,3,4,6,其魔法值分别为5,7,28,29。以物品5为例,它作为A物品出现了1次,作为B物品出现了3次,没有作为C物品或者D物品出现,所以这一行输出的四个数依次为1,3,0,0。此外,如果我们将输出看作一个m行4列的矩阵,那么每一列上的m个数之和都应等于魔法阵的总数。所以,如果你的输出不满足这个性质,那么这个输出一定不正确。你可以通过这个性质在一定程度上检查你的输出的正确性。
题解:
85分方法:
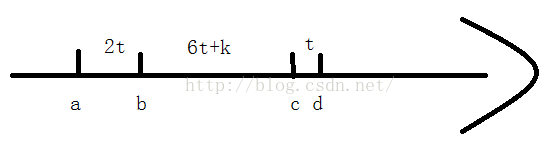
由xa<xb<xc<xd,Xb-Xa=2(Xd-Xc),并且xb-xa<(xc-xb)/3可得:
(以下xa,xb,xc,xd简称a,b,c,d)
b-a=2(d-c), 3(b-a)=c-b+k (0<k)
设d-c为t,则把a,b,c,d位置画成数轴形式:
由此看出,只需枚举t,a,k,再判断得出的a,b,c,d四个魔法值是否存在,
存在则对应答案数组加上除自己之外其它三个魔法值存在的个数的乘积
枚举范围:
1<=t<=(n-1)/9;
1<=k<=n-9t;
1<=a<=n-9t-k;
85分参考程序:
var i,t,k,n,m,xa,xb,xc,xd:longint;
a:array[1..40000]of longint;
b:array[1..15000,1..4]of int64;
c:array[1..15000]of longint;
begin
assign(input,'magic.in');reset(input);
assign(output,'magic.out');rewrite(output);
readln(n,m);
for i:=1to m do
begin
readln(a[i]);
inc(c[a[i]]);
end;
for i:=1 to n do
begin
xa:=i;
if c[xa]=0 then continue;
for t:=1 to (n-1-i) div 9 do
begin
xb:=i+2*t;
if c[xb]=0 then continue;
for k:=1 to n-i-9*t do
begin
xc:=i+8*t+k;
if c[xc]=0 then continue;
xd:=xc+t;
if c[xd]=0 then continue;
b[xa,1]:=b[xa,1]+c[xb]*c[xc]*c[xd];
b[xb,2]:=b[xb,2]+c[xa]*c[xc]*c[xd];
b[xc,3]:=b[xc,3]+c[xa]*c[xb]*c[xd];
b[xd,4]:=b[xd,4]+c[xa]*c[xb]*c[xc];
end;
end;
end;
for i:=1 to m do
writeln(b[a[i],1],' ',b[a[i],2],' ',b[a[i],3],' ',b[a[i],4]);
close(input);close(output);
end.
100分题解:
以下为转载内容:
http://blog.csdn.net/gmh77/article/details/53347826
尝试把三重循环降到两重循环。
根据上面可以得知,我们其实只要枚举一个A和t,接下来把所有符合条件的CD求出计算。
可以用后缀和来实现这一想法。
设SUM[i]表示从i~n-i之间所有的CD对的乘积。
因为A和B是已知的,而CD却是不定的,所以先用后缀和求出A和B的方案数。
为了求出最多的方案数,假设k=1。
因为AB为2t,BC至少为6t+1,所以C至少为A+8t+1。
接下来再把之前的公式合并一下,就变成了这样:
方案数A=Wb*Sum[A+t*8+1](所有的Wc*所有的Wd)
同理,方案数B和方案A近似,只不过Wb要变成Wa。
接下来求CD的方案。
把刚才的方法改一下,用前缀和计算出所有的AB对的乘积,再枚举C的位置(D的话改一下也可以)
只不过A和B的距离为2i,所以计算前缀和时要这样算:
Sum[j]=Sum[j-1]+W[j]*W[j-2*t]
BC间隔至少为6t+1,所以B最大为C-6t-1。
所以C的方案数就是Wd*Sum[C-6*t-1](所有的Wa*所有的Wb)
D就不用讲了吧。
最后把每个对应的次数输出就行了。
100分参考代码:
注:本题实现代码可能与题解方法不完全相符
var a:array[0..40000]of longint;
b,d:array[0..15000]of int64;
c:array[0..15000,1..4]of int64;
i,j,n,m,t:longint;
begin
assign(input,'magic.in');reset(input);
assign(output,'magic.out');rewrite(output);
readln(n,m);
for t:=1 to m do
begin
readln(a[t]);
inc(b[a[t]]);
end;
for t:=1 to (n-1) div 9 do
begin
fillchar(d,sizeof(d),0);
for j:=n-t downto 8*t+1 do
d[j]:=d[j+1]+b[j]*b[j+t];
for j:=1 to n-9*t-1 do
begin
c[j,1]:=c[j,1]+b[j+2*t]*d[j+8*t+1];
c[j+2*t,2]:=c[j+2*t,2]+b[j]*d[j+8*t+1];
end;
fillchar(d,sizeof(d),0);
for j:=1 to n-9*t-1 do
d[j]:=d[j-1]+b[j]*b[j+2*t];
for j:=n-t downto 8*t+1 do
begin
c[j,3]:=c[j,3]+b[j+t]*d[j-8*t-1];
c[j+t,4]:=c[j+t,4]+b[j]*d[j-8*t-1];
end;
end;
for i:=1 to m do
writeln(c[a[i],1],' ',c[a[i],2],' ',c[a[i],3],' ',c[a[i],4]);
close(input);close(output);
end.






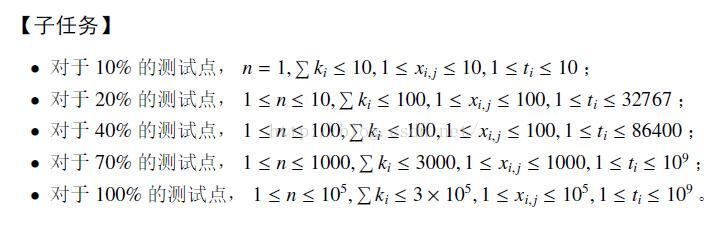














 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








