【编译原理】语法分析（四）

本文是语法分析的第四篇文章，第一篇文章介绍了基本的文法、推导和归约的概念，第二篇文章介绍了自顶向下的语法分析和LL(1)方法，第三篇文章介绍了自底向上的语法分析和SLR方法。本文将承接第三篇文章，介绍比SLR更为强大的LR方法。

PS：阅读本文需要掌握前三篇文章的知识，建议读者先阅读前三篇文章。

文法&约定

老规矩，先给出一个贯穿全文的文法G：

    S→L=R|R
    L→*R|id
    R→L

以及该文法的增广形式：

    S'→S
    S→L=R|R
    L→*R|id
    R→L

并为产生式标号：

    (1) S→L=R    (2) S→R    (3) L→*R
    (4) L→id     (5) R→L

以下是下文使用的符号约定：

• 大写字母：表示非终结符号，如A、B、C等；
• 小写字母：表示终结符号，如a、b、c等；
• 希腊字母：表示由终结符号和非终结符号组成的串或者空串，如α、β、γ等；
• 开始符号：用S表示文法的开始符号；
• 结束符号：用$表示结束标记，如输入结束、栈为空等。

SLR的不足

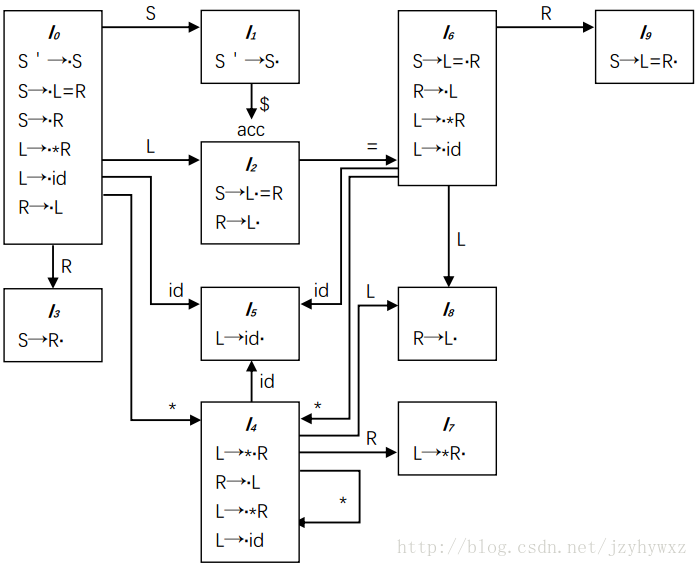
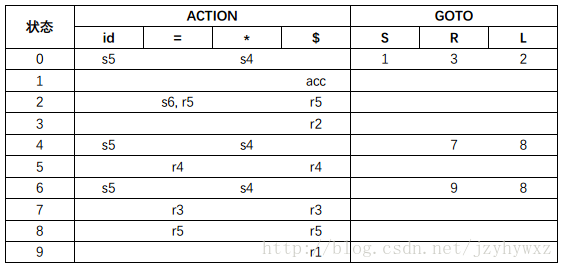
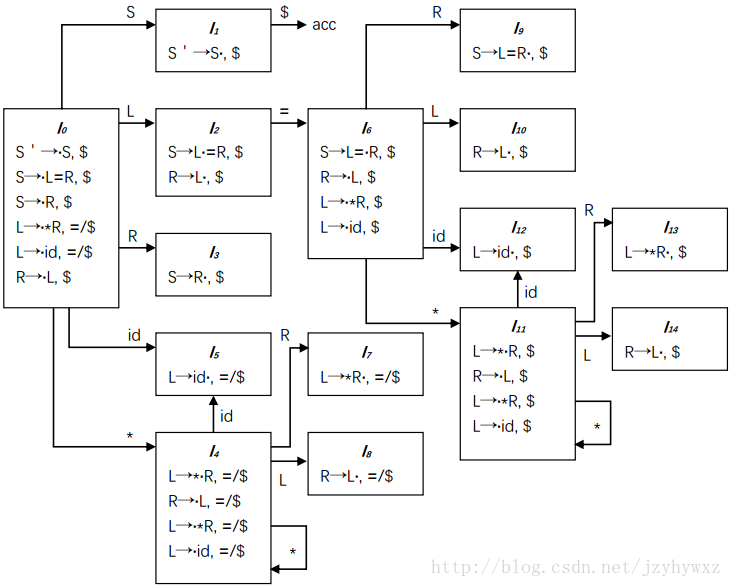
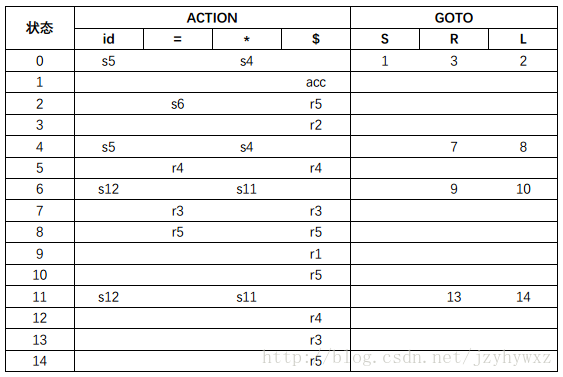
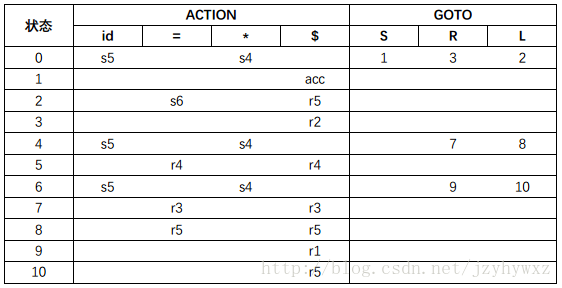
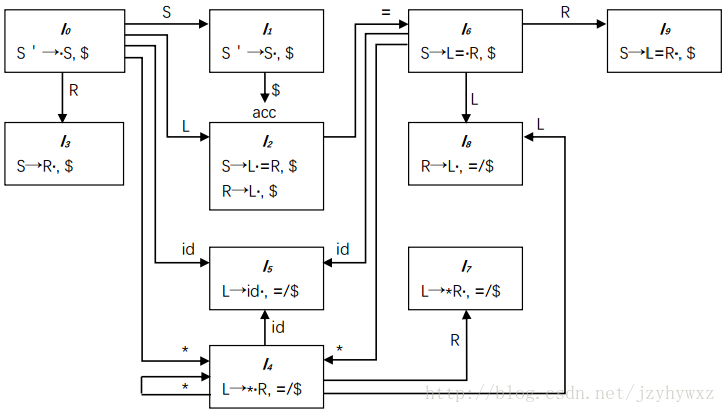
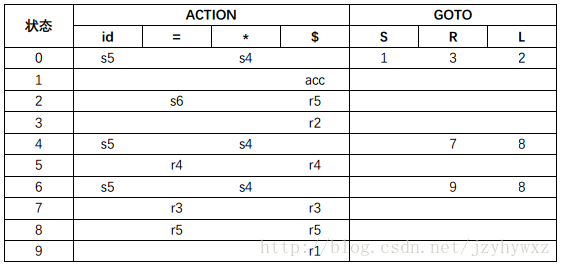
SLR虽然足够简单（不然怎么会叫简单LR），但是它的功能还不够强大。考虑文法G，为它构造LR(0)自动机和LR语法分析表（如果不知道如何构造，请先阅读第三篇文章）：

在语法分析表中，si表示移入状态i，rj表示按照第j个产生式归约。注意到，状态2在输入符号“=”上有s6和r5两个动作，这里产生了一个移入/归约冲突。但是，文法G不是二义性的，只能说SLR还不够强大。

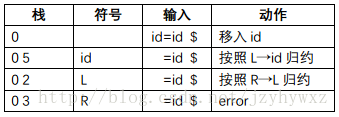
如果把状态2在输入符号“=”上的动作规定为r5，那么对串id=id，它的语法分析过程为：

可以看到，语法分析器最后报告了一个错误。

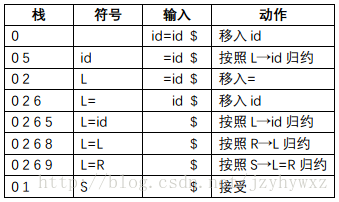
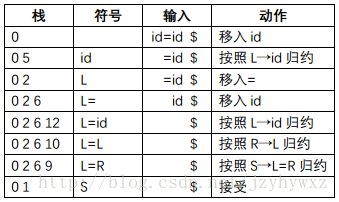
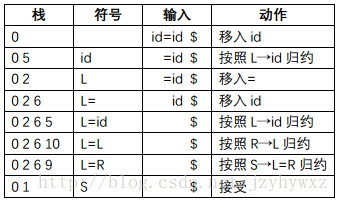
如果把状态2在输入符号“=”上的动作规定为s6，那么它的语法分析过程变为：

语法分析器最终接受了串id=id。

为了让语法分析器对有冲突的选项选择正确的动作，我们需要一种更强大的LR技术。

规范LR方法

规范LR方法和SLR方法类似，它也会构造一个自动机，并从这个自动机得到语法分析表。但是，它们用于构造自动机的项集族不同，SLR方法使用规范LR(0)项集族构造一个自动机，而规范LR方法使用规范LR(1)项集族构造一个自动机。

规范LR(1)项

形如[A→α·β, a]的项是一个规范LR(1)项，其中，第一个分量是一个规范LR(0)项，第二个分量是一个终结符号或$，它表示这个规范LR(1)项的向前看符号。在形如[A→α·β, a]且β≠ε的项中，向前看符号没有任何作用，但是在形如[A→α·, a]的项中，只有在下一个输入符号为a时才会按照A→α进行规约。

规范LR(1)自动机

构造LR(1)自动机也用到了CLOSURE和GOTO函数，只不过它们的规则有所改变。

计算一个规范LR(1)项集I的CLOSURE集合，按照如下规则进行：

1. 将I中的所有项加入CLOSURE集合中；
2. 对I中每个形如[A→α·Bβ, a]的项，首先找到产生式头为B的每个产生式B→γ，然后找到FIRST(βa)中的每个终结符号b，最后将所有[B→γ, b]加入CLOSURE集合中；
3. 重复上面的步骤，直到没有新的项可以加入CLOSURE集合中为止。

计算一个规范LR(1)项集I的GOTO集合，按照如下规则进行：

1. 对I中每个形如[A→α·Xβ, a]的项，将[A→αX·β, a]加入GOTO集合中；
2. 把GOTO集合作为CLOSURE函数的参数，计算GOTO集合的闭包。

下面我们对文法G构造LR(1)自动机：

我们发现LR(1)自动机比LR(0)自动机多了5个状态，通常情况下，LR(1)自动机的状态数要比LR(0)自动机的状态数多得多。

规范LR(1)语法分析表

规范LR(1)语法分析表也是由ACTION和GOTO函数组成的，但是，它的ACTION函数规则与LR(0)不同。

对一个规范LR(1)自动机，按照如下规则设置状态i上的动作：

1. 如果[A→α·aβ, b]在Ii中，并且GOTO(Ii, a)=Ij，那么将ACTION[i, a]设置为“移入j”，这里的符号a必须是一个终结符；
2. 如果[A→α·, a]在Ii中且A≠S’，那么将ACTION[i, a]设置为“按照A→α归约”；
3. 如果[S'→S·, $]在Ii中，那么将ACTION[i, $]设置为“接受”；
4. 其它所有空白的ACTION条目都设置为“报错”。

对一个规范LR(1)自动机，按照如下规则设置状态i上的转移：

1. 如果GOTO(Ii, A)=Ij，那么GOTO[i, A]=j，这里的第一个GOTO是规范LR(1)自动机的GOTO集合；
2. 其它所有空白的GOTO条目都设置为“报错”。

下面我们从文法G的LR(1)自动机构造规范LR(1)语法分析表：

现在再用这张表对输入串id=id做语法分析：

可以发现规范LR(1)语法分析器最终接受了串id=id。

规范LR方法的问题

规范LR方法可以说是最通用的为文法构造LR语法分析表的技术，但是，它的一个问题是会产生大量的状态。那么，有没有什么方法能够减少规范LR语法分析表的状态数呢？

我们看一看上面文法G的LR(1)自动机，发现状态4和状态11非常相似，如果忽略向前看符号，它们就是相同的状态，状态5和状态12，状态7和13，状态8和14，也有相同的特点。

如果把具有这样的特点的所有项集合并成一个，那么状态数就能够大大减少。现在的问题是，我们要如何表述这个特点。直接地说，如果两个规范LR(1)项集，忽略其中每个项的向前看符号后，这两个项集中包含相同的项，那么这两个项可以合并成一个。进一步的，我们可以比较这两个项集的“核心项”的集合，从而判断这两个项集是否能够合并。

判断一个规范LR(0)项是否是核心项，使用如下两条规则：

1. 如果这个项是初始项S’→·S，那么这个项是核心项；
2. 如果这个项中的“·”不在最左端，那么这个项是核心项。

换句话说，对一个项集I，假设I的核心项集为K，那么CLOSURE(K)=I。这里的项是规范LR(0)项，对规范LR(1)项来说，忽略向前看符号后就是一个规范LR(0)项。

现在我们可以正式定义这个特点了。对一个规范LR(1)语法分析表（器）中的所有状态，按照如下规则进行合并：

1. 把每个项集Ii替换为其核心项集Ki，如果两个项集Km和Kn忽略向前看符号后包含相同的规范LR(0)项，那么Km和Kn是相似的；
2. 如果两个核心项集Km和Kn相似，那么将Km和Kn合并成一个新项集Kmn。对Km中的每个规范LR(1)项[A→α·β, a]，其在Kn中对应于项[A→α·β, b]，将[A→α·β, a/b]放入Kmn中；
3. 重复上面的步骤，直到没有任意两个核心项集可以合并为止；
4. 计算每个核心项集的CLOSURE集合。

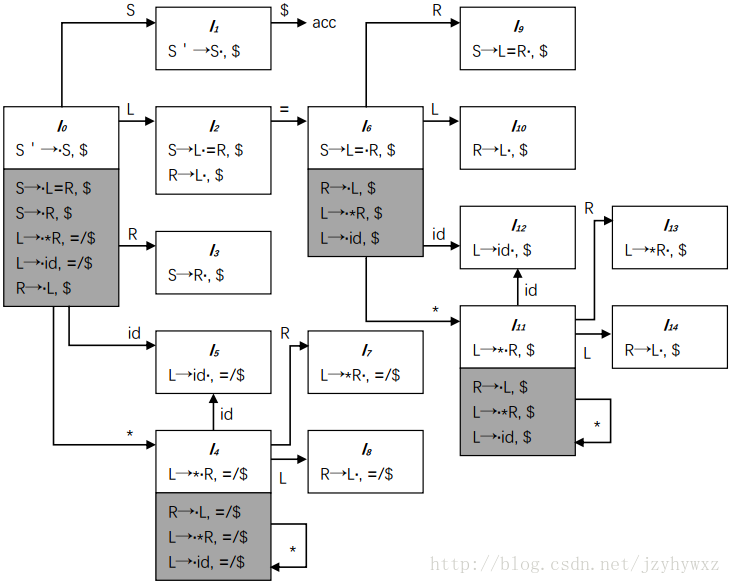
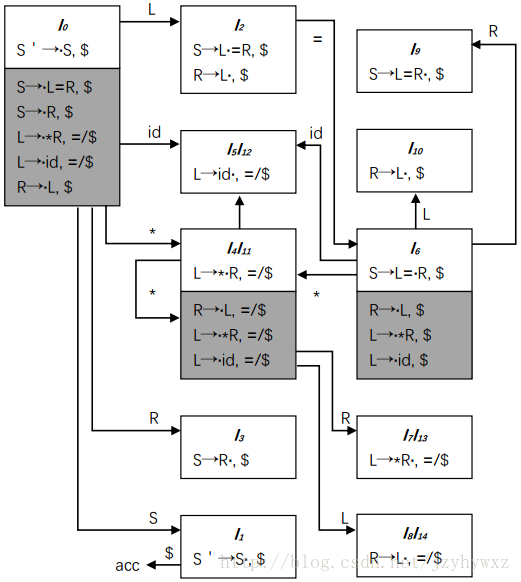
现在我们尝试对文法G的规范LR(1)自动机进行化简，首先找出其中每个项集的核心项集：

其中，白色背景的项集是核心项集，灰色背景的项集是非核心项集。我们发现，I4与I11、I5与I12、I7与I13、I8与I14是相似的，将它们合并后得到：

合并后的自动机只有11个状态，比合并前少了4个状态。下面是根据合并后的LR(1)自动机得到的语法分析表：

这里用编号在前的状态表示合并的状态，例如状态4表示状态4&11。用这张表对串id=id进行语法分析：

可以发现，化简前后的规范LR(1)语法分析器都接受了输入串id=id，但是化简后的规范LR(1)语法分析器需要维护的状态变少了。实际上，化简后的规范LR(1)语法分析器是一个LALR语法分析器。

LALR方法

“向前看LR”方法，即LALR方法，它基于LR(0)项集族，通过向LR(0)项中引入向前看符号构造LALR语法分析表。使用LALR方法可以比SLR文法处理更多的文法，同时构造得到的语法分析表不比SLR分析表大。在很多情况下，LALR方法是最合适的选择。

我们可以对上一节介绍的合并项集的方法进行修改，使得在创建LALR语法分析表的过程中不需要构造出完整的规范LR(1)项集族：

1. 只使用内核项来表示任意的LR(0)或LR(1)项集，即[S'→·S]或[S'→·S, $]以及“·”不在产生式体最左端的项；
2. 使用一个“传播和自发生成”的过程来生成向前看符号，根据LR(0)项的内核生成LALR(1)项的内核；
3. 使用CLOSURE函数对每个LALR(1)内核项集求闭包，得到规范LR(1)项集族，用该项集族就能构造LALR(1)语法分析表。

PS：在LALR方法中使用的CLOSURE和GOTO函数与规范LR方法中的相同。

生成向前看符号可以分为两种情况，一种是自发生成的，一种是传播的。对一个规范LR(1)核心项集I，假设它包含项[A1→α1·β1, a1]、[A2→α2·β2, a2]、…、[An→αn·βn, an]，对文法符号X计算J=GOTO(CLOSURE(I), X)，假设J中包含一个项[B→γ·δ, b]，则有：

• 如果b≠ai（1<=i<=n），那么说向前看符号b对于B→γ·δ是自发生成的；
• 如果b=ai（1<=i<=n），那么说向前看符号b从I的内核中的Ai→αi·βi传播到了J的内核中的B→γ·δ上。

对一个LR(0)项集I的内核项集K以及一个文法符号X，使用如下方法确定向前看符号：

现在可以把向前看符号附加在LR(0)项集的内核上，从而得到LALR(1)项集。首先，我们知道$是初始LR(0)项集中的S’→·S的向前看符号，使用上面的方法可以得到所有自发生成的向前看符号；接着，将所有这些向前看符号列出后，我们必须让它们不断传播，直到不能继续传播为止。下面给出了一个传播方法：

1. 构造LR(0)项集族的内核；
2. 对每个LR(0)项集的内核K和每个文法符号X，计算GOTO(CLOSURE(K), X)，确定GOTO(CLOSURE(K), X)中各个项的哪些向前看符号是自发生成的，并确定传播的向前看符号从I中的哪个项被传播到GOTO(CLOSURE(K), X)中的哪个项上的；
3. 初始化一个表格，表中给出了每个项集中的每个内核项相关的向前看符号。最初，每个项的向前看符号只包括那些在步骤（2）中确定为自发生成的符号；
4. 不断扫描所有项集的内核项。当我们访问一个项i时，使用步骤（2）中得到的信息，确定i将它的向前看符号传播到了哪些内核项中。项i的当前向前看符号集合被加到和这些被传播的内核项相关联的向前看符号集合中。继续在内核项上进行扫描，直到没有新的向前看符号被传播为止。

我们还是用例子来说明如何使用LALR方法。对文法G使用LALR方法。

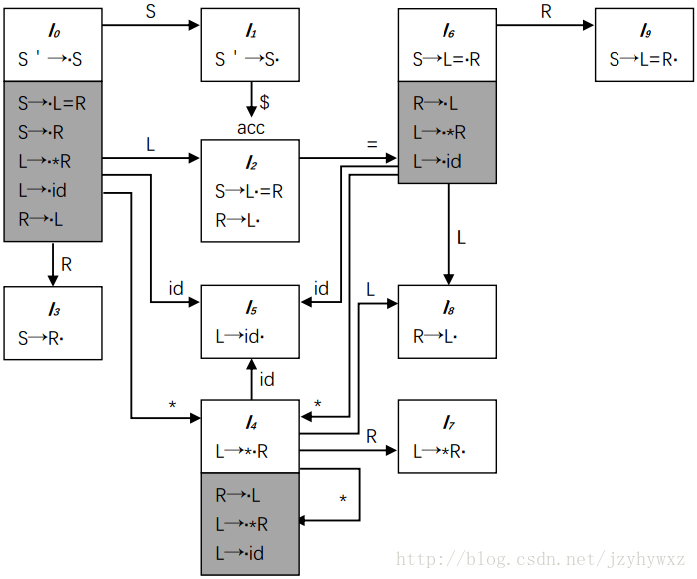
第一步，构造它的LR(0)项集族的内核，这里我们用一个LR(0)自动机表示：

白色背景是LR(0)内核项集，灰色背景不是LR(0)内核项集，并且这个自动机中已经给出了每个项集的GOTO函数。初始时，I0对应的LR(1)内核项集为{ [S'→·S, $] }；

第二步，计算CLOSURE({ [S'→·S, #] })得到：

    S'→·S, #
    S→·L=R, #
    S→·R, #
    L→·*R, =
    L→·id, =
    R→·L, #

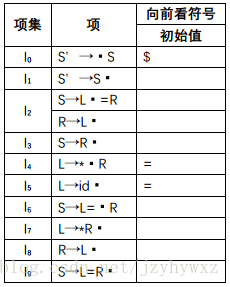
因此，“$”是传播的向前看符号，“=”是自发生成的向前看符号。我们有，“$”从I0的[S'→·S, $]，传播给I1的[S'→S·, $]、I2的[S→L·=R, $]、I2的[R→L·, $]和I3的[S→R·, $]；“=”在I4的[L→*·R, =]和I5的[L→id·, =]上是自发生成的。现在我们初始化表格，由于这个表格一开始只包含自发生成的向前看符号，因此表格初始化为：

第三步，开始进行第一趟传播，由于在上一步中已经知道了“$”的传播，因此我们只计算“=”的传播。计算CLOSURE({ [L→*·R, #] })得到：

    L→*·R, #
    R→·L, #
    L→·*R, #
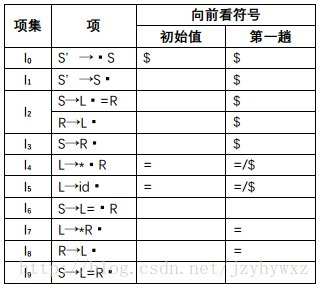
    L→·id, #

我们有，“=”从I4的[L→*·R, =]传播给I4的[L→*·R, =]、I5的[L→id·, =]、I7的[L→*R·, =]和I8的[R→L·, =]。另外，由于I5的[L→id·, =]已经没有计算闭包的必要，因此经过第一趟传播后表格变为：

第四步，开始进行第二趟传播，我们发现，只有I2的[S→L·=R, $]需要计算闭包。计算CLOSURE({ [S→L·=R, #] })得到：

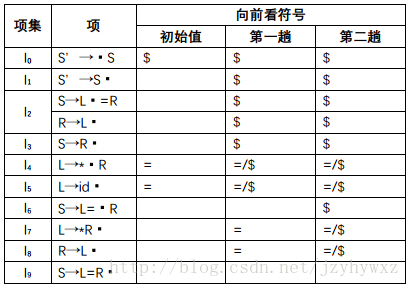
    S→L·=R, #

我们有，“$”从I2的[S→L·=R, $]传播给I6的[S→L=·R, $]。另外，由于I4多了一个[L→*·R, $]，因此经过第二趟传播后表格变为：

第五步，开始进行第三趟传播，我们发现，只有I6的[S→L=·R, $]需要计算闭包。计算CLOSURE({ [S→L=·R, #] })得到：

    S→L=·R, #
    R→·L, #
    L→·*R, #
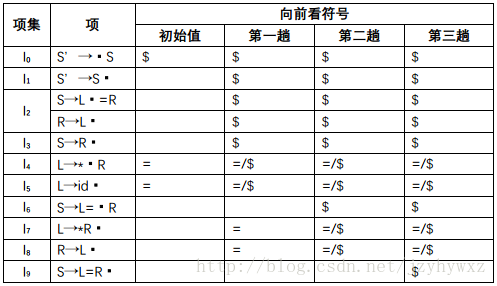
    L→·id, #

我们有，“$”从I6的[S→L=·R, $]传播给I4的[L→*·R, $]、I5的[L→id·, $]、I8的[R→L·, $]和I9的[S→L=R·, $]。因此经过第三趟传播后表格变为：

第六步，我们发现传播不能继续进行了，现在我们把表中的向前看符号加入到LR(0)自动机中，得到LALR(1)自动机：

第七步，根据LALR(1)自动机，可以构造LALR语法分析表。这里构造分析表的规则与构造规范LR语法分析表的规则一样，得到文法G的LALR语法分析表如下：

可以看到，相比于SLR语法分析表，LALR语法分析表中的状态2对符号“=”没有移入/规约冲突，而且两张表的状态数相同。

欢迎关注微信公众号fightingZh(≖ᴗ≖)✧