（DFS/并查集）Codeforces Round #479 (Div. 3) E. Cyclic Components

本文链接：https://blog.csdn.net/kaisa158/article/details/80486108

You are given an undirected graph consisting of $n$ vertices and $m$ edges. Your task is to find the number of connected components which are cycles.

Here are some definitions of graph theory.

An undirected graph consists of two sets: set of nodes (called vertices) and set of edges. Each edge connects a pair of vertices. All edges are bidirectional (i.e. if a vertex $a$ is connected with a vertex $b$ , a vertex $b$ is also connected with a vertex $a$ ). An edge can't connect vertex with itself, there is at most one edge between a pair of vertices.

Two vertices $u$ and $v$ belong to the same connected component if and only if there is at least one path along edges connecting $u$ and $v$ .

A connected component is a cycle if and only if its vertices can be reordered in such a way that:

the first vertex is connected with the second vertex by an edge,
the second vertex is connected with the third vertex by an edge,
...
the last vertex is connected with the first vertex by an edge,
all the described edges of a cycle are distinct.

A cycle doesn't contain any other edges except described above. By definition any cycle contains three or more vertices.

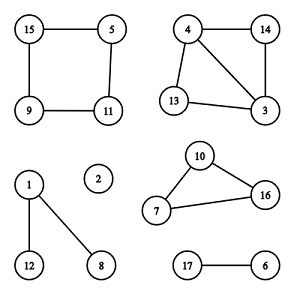$\text{[math]}$ There are

6

connected components,

2

of them are cycles:

[7, 10, 16]

and

[5, 11, 9, 15]

Input

The first line contains two integer numbers $n$ and $m$ ( $1 \leq n \leq 2 \cdot 10^{5}$ , $0 \leq m \leq 2 \cdot 10^{5}$ ) — number of vertices and edges.

The following $m$ lines contains edges: edge $i$ is given as a pair of vertices $v_{i}$ , $u_{i}$ ( $1 \leq v_{i}, u_{i} \leq n$ , $u_{i} \neq v_{i}$ ). There is no multiple edges in the given graph, i.e. for each pair ( $v_{i}, u_{i}$ ) there no other pairs ( $v_{i}, u_{i}$ ) and ( $u_{i}, v_{i}$ ) in the list of edges.

Output

Print one integer — the number of connected components which are also cycles.

Note

In the first example only component $[3, 4, 5]$ is also a cycle.

The illustration above corresponds to the second example.

题解：

求环的个数，每个节点的度一定为2.

DFS：

#include <iostream>
#include <string.h>
using namespace std;

const int maxn = 200005;
int Map[maxn][maxn];
int vis[maxn],d[maxn];
int len,flag;
int n,m,sum;

int dfs(int t,int l)
{
	// if(flag == 1)
	if(flag==1)
		return 1;
	// 	return;
	for(int j=1;j<=n;j++)
	{
		if(Map[t][j]==1 && d[j]==2)
		{
			if(vis[j]==1 && l>1)
			{
				flag = 1;
				sum++;
				return 1;
			}
			//if()
			if(vis[j]==0)
			{
				vis[j]=1;
				//int t1 = ;
				//dfs(j,l+1);
				if(!dfs(j,l+1))
				{
					vis[j]=0;
				}
			}
		}
	}
	return 0;
}

int main()
{
	int u,v;
	sum=0;
	cin >> n >> m;
	for(int i=0;i<=n;i++)
	{
		d[i]=0;
		vis[i]=0;
		for(int j=0;j<=n;j++)
		{
			Map[i][j]=0;
		}
	}
	for(int i=1; i<=m; i++)
	{
		cin >> u >> v;
		d[u]++;
		d[v]++;
		Map[u][v]=1;
		Map[v][u]=1;
	}
	//len=0;flag=0;
	for(int i=1; i<=n; i++)
	{
		len=0;flag=0;
		if(vis[i]==0)
		{
			vis[i]=1;
			if(dfs(i,len)==0)
			{
				vis[i]=0;
			}
		}
		for(int j=1;j<=n; j++)
			cout<<vis[j]<< " ";
		cout<<endl;
	}
	cout<<sum<<endl;
	return 0;
}

并查集：

#include<iostream>
#include<string.h>
using namespace std;
const int maxn = 200005;

struct node
{
	int u,v;
}e[maxn];

int n,m;
int d[maxn],f[maxn];
int k;

int Find(int fa)
{
	if(f[fa]==fa)
		return fa;
	return f[fa] = Find(f[fa]);
}

void Union(int a,int b)
{
	int fa = Find(a);
	int fb = Find(b);
	if(fa == fb)
		k++;
	else
		f[fa] = fb;
}

int main()
{
	cin>>n>>m;
	k=0;
	memset(d,0,sizeof(d));
	for(int i=1;i<=n;i++)
	{
		f[i] = i;
	}
	for(int i=1;i<=m;i++)
	{
		cin>>e[i].u>>e[i].v;
		// if(e[i].u==e[i].v)
		// 	continue;
		d[e[i].u]++;
		d[e[i].v]++;
	}
	for(int i=1;i<=m;i++)
	{
		if(d[e[i].u]==2 && d[e[i].v]==2)
		{
			Union(e[i].u,e[i].v);
		}
	}
	cout << k << endl;
	return 0;
}