线性表之循环双链表

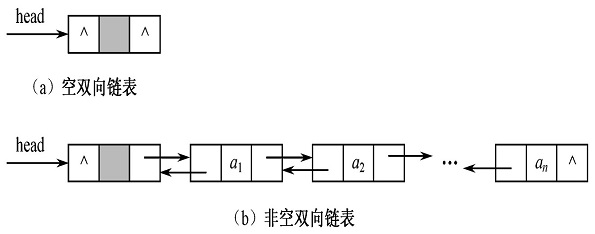
    在循环链表中，虽然从任一结点出发均可以扫描到其他结点，但是要找到其前驱结点则需要遍历整个链表。如果希望快速确定表中任一结点的前驱结点，可以再每个结点中再设置一个指向其前驱结点的指针域，这样就形成的双链表(doubly linked list)，如第一张图所示，prior为前驱指针域，next为后继指针域。

   结点的C++描述为：

template<class Type>
struct DulNode
{
	Type data;																		//数据域
	DulNode<Type> *prior, *next;	        //指向前驱结点的指针和指向后继结点的指针
};

    和单链表类似，双链表一般也是由头指针唯一确定，增加头结点也能使双链表的某些操作变得方便，将头结点和尾结点链接起来就构成了循环双链表，这样无论是插入还是删除操作，对链表中开始结点、终端结点和中间结点的操作过程相同。实际上常用带头结点的循环双链表，实现如下：

dullinklist类的声明：

template<class Type>
class Dullist{
private:
	DulNode<Type>* first;																//头指针指向头结点
public:
	Dullist();																	//显示默认构造函数
	Dullist(Type a [], int len);	//构造函数
	~Dullist();			//析构函数
	int getLength();		//求双链表的长度
	Type Get(int i);		//按位查找数据
	int Locate(Type x);		//按值查找数据位置
	void Insert(int i, Type x);	//在线性表第i个位置上插入值为x的结点
	Type Delete(int i);		//删除第i个元素
	void Print();			//遍历循环双链表
	bool isEqual();			//判断循环双链表是否是对称
																			
};

类实现：

template<class Type>
Dullist<Type>::Dullist(){
	first = new DulNode<Type>;
	first->next = first;
	first->prior = first;
}

template<class Type>
Dullist<Type>::Dullist(Type a [], int len){
	first = new DulNode<Type>;
	first->next = first;
	first->prior = first;
	DulNode<Type>* r = first;
	for (int i = 0; i < len; i++){
		DulNode<Type>* s = new DulNode<Type>;
		s->data = a[i];
		r->next = s;
		s->prior = r;
		r = s;
	}
	r->next = first;
	first->prior = r;
}

template<class Type>
Dullist<Type>::~Dullist(){
	int len = getLength();
	DulNode<Type>* p = first;
	while (len+1){
		p = first;
		first = first->next;
		delete p;
		len--;
	}
}

template<class Type>
int Dullist<Type>::getLength(){
	int count = 0;
	DulNode<Type>* p = first->next;
	while (p != first){
		count++;
		p = p->next;
	}
	return count;
}

template<class Type>
void Dullist<Type>::Print(){
	cout<< "头结点";
	DulNode<Type>* p =first->next;
	while (p != first){
		cout << "-->" << p->data;
		p = p->next;
	}
	cout << "-->头结点" << endl;
}

template<class Type>
Type Dullist<Type>::Get(int i){
	int count = 1;
	DulNode<Type>* p = first->next;
	while (p != first&&count < i){
		count++;
		p = p->next;
	}
	if (p == first)throw"位置";
	else{
		return p->data;
	}
}

template<class Type>
int Dullist<Type>::Locate(Type x){
	int count = 1;
	DulNode<Type>* p = first->next;
	while (p != first){
		if (p->data == x)return count;
		p = p->next;
		count++;
	}
	return 0;
}

template<class Type>
void Dullist<Type>::Insert(int i, Type x){
	int count = 0;
	DulNode<Type>* p = first;
	while (count < i - 1){
		p = p->next;
		count++;
	}
	DulNode<Type>* s = new DulNode<Type>;
	s->data = x;
	s->prior = p;
	s->next = p->next;
	p->next->prior = s;
	p->next = s;
}

template<class Type>
Type Dullist<Type>::Delete(int i){
	DulNode<Type>* p = first;
	int count = 0;
	while (count < i ){
		p = p->next;
		count++;
	}
	if (p == first)throw"位置";
	else{
		p->prior->next = p->next;
		p->next->prior = p->prior;
		delete p;
	}
}

template<class Type>
bool Dullist<Type>::isEqual(){
	DulNode<Type>* p = first->next;
	DulNode<Type>* q = first->prior;
	while (p != q&&p->prior != q){
		if (p->data == q->data){
			p = p->next;
			q = q->prior;
		}
		else return false;
	}
	return true;
}

main.cpp

#include "dullist.cpp"
#include "dullist.h"
int main(){
	int a[7] = { 1, 2, 3, 4,3,2,1 };
	Dullist<int> dl(a, 7);
	dl.Print();
	cout << "dl的长度是：" << dl.getLength() << endl;
	cout << "第6个结点是：" << dl.Get(6) << endl;
	cout << "4是第" << dl.Locate(4) << "个结点" << endl;
	dl.Insert(4, 10);
	cout << "在第四个位置上插入10：";
	dl.Print();
	dl.Delete(1);
	cout << "删除第1个结点：";
	dl.Print();
	cout << "dl" << (dl.isEqual() == true ? "是" : "不是") << "对称的" << endl;
	return 0;
}

测试结果：