扩展欧几里得定理

扩展欧几里德算法（注意：拓展（扩展）欧几里得算法是求解形如ax+by=1的方程组的（而且a和b是互质的，允许通过约分得到，并且求出的x如果是正数的话那一定是最小正整数，如果为负，那加上b的绝度值之后也是满足方程组的最小正整数解），要想求解形如ax+by=n (n!=1) 的方程组，必须先化成ax+by=1（而且a和b是互质的，允许约分）这种形式。最后求出的结果是ax+by=1的结果，那就再乘上n倍即可。

具体步骤 ：

ax  +  by  =  n的步骤如下: 

(1)计算gcd(a,  b).  若gcd(a, b)不能整除n，则方程无整数解；否则，在方程的两边同除以gcd(a, b)，

  得到新的不定方程a'x  +  b'y =  n'，此时gcd(a',  b')  =  1 

(2)求出不定方程a'x  +  b'y  =  1的一组整数解x0,  y0，则n'x0，n'y0是方程a'x  +  b'y  =  n'的一组整数解。 

(3)可得方程a'x +  b'y  =  n'的所有整数解为： 

    x  =  n'x0  +  b't 
    y  =  n'y0  -  a't    (t为整数) 

这也就是方程ax  +  by  =  n的所有整数解 

举个栗子

假如求2x+4y=6的所有解，那么就先两边同时除以,2得到x+2y=3,然后计算x+2y=1的解（缩小了3倍，而且一般考虑到实际情况x会为正整数）x=1,y=0,

但是目的不是求这个，而是它2x+4y=6，所以结果x=1,y=0 再乘以3（因为前面缩小过3倍，所以记得再扩大3倍嘛）得到的x=3，y=0 就是x+2y=3的解，

这也就是2x+4y=6的一个解（只是约分了而已）

总之拓展（扩展）欧几里得算法它求出的是x+2y=1的解，想要求其他问题，你只能借助它来求。

如果gcd(a,b)=d，则存在m,n，使得d = ma + nb，称呼这种关系为a、b组合整数d，m，n称为组合系数。

特殊情况：当最大公约数d=1时，有 ma + nb = 1 ，此时可以看出m是a模b的乘法逆元，n是b模a的乘法逆元。

对于正整数和，如果有，那么把这个同余方程中的最小正整数解叫做模的逆元。

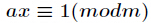
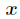
逆元一般用扩展欧几里得算法来求得，如果为素数，那么还可以根据费马小定理得到逆元为。（都要求a和m互质）

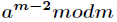
a和b互质是指，a,b的最大公约数只有1，前提是a,b都是正整数，那这两个正整数互质

基本算法：对于不完全为 0 的非负整数 a，b，gcd（a，b）表示 a，b 的最大公约数，必然存在整数对 x，y ，使得 gcd（a，b）=ax+by。

证明：设 a>b。

　　1，显然当 b=0，gcd（a，b）=a。此时 x=1，y=0；

　　2，ab!=0 时

　　设 ax1+by1=gcd(a,b);

　　bx2+(a mod b)y2=gcd(b,a mod b);

　　根据朴素的欧几里德原理有 gcd(a,b)=gcd(b,a mod b);

　　则:ax1+by1=bx2+ (a mod b)y2;

　　即:ax1+by1=bx2+ (a-(a/b)*b)y2=ay2+bx2-(a/b)*by2;//红色部分是相等的

　　根据恒等定理得：x1=y2; y1=x2-(a/b)*y2;

     这样我们就得到了求解 x1,y1 的方法：x1，y1 的值基于 x2，y2.

　  上面的思想是以递归定义的，因为 gcd 不断的递归求解一定会有个时候 b=0，所以递归可以结束。

int exgcd(int a,int b,int &x,int &y)
{
    if(b==0)
    {
        x=1;
        y=0;
        return a;//如果b等于0，直接返回a就结束.否则就继续下面进行递归
    }
    int r=exgcd(b,a%b,x,y);//继续递归，
    //下面这里是所有递归结束后才进行的，也就是说只执行了一次，它们是不在递归里面的，一句话，最后执行一次且只执行一次，不要认为它们也跟着递归了                int t=x;
    x=y;
    y=t-a/b*y;
    return r;//r是最大公约数，x是a的逆元,y是b的逆元
}

#include <iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
int x,y,q;
void ex_Eulid(int a,int b,int &x,int &y)
{
    if(b==0)
    {
        x=1;
        y=0;
        q=a;
    }
    else
    {
        ex_Eulid(b,a%b,x,y);
        double temp=x;
        x=y;
        y=temp-a/b*y;
    }
}
int main()
{
    int a,b;
    while(cin>>a>>b)//求解形如a*x+b*y=gcd(a,b)的方程
    {
        ex_Eulid(a,b,x,y);
        printf("%d=(%d)*%d+(%d)*%d\n",q,x,a,y,b);
        printf("%d的逆元:%d\n",a,x);
        printf("%d的逆元:%d\n",b,y);
    }
    return 0;
}

应用
1：解方程ax+by=gcd(a,b)

2：解不定方程ax+by=c

定理二：对于不定整数方程ax+by=c ，若 c mod gcd(a,b)=0,则该方程存在整数解，否则不存在整数解。 
故当c mod gcd(a,b)=0，先用扩展欧几里得算法求出ax+by=gcd(a,b)的一组解x1,y1。
则x2=x1*c/gcd(a,b)，y2=y1*c/gcd(a,b)为ax+by=c的一组解。
x=x2+b/gcd(a,b)*t,y=y2-a/gcd(a,b)*t,(t为整数)，即为ax+by=c的所有解。