BZOJ2088 POI2010 Teleportation

---

反省一下自己最近的状况。

发现自己写yy题和dp题的水平有所下降（本来就没多高还掉，跟我昨天刚掉的CFrank一样），最近几天的比赛和写题目都非常不顺心。这几天尽量突破逆境吧。

---

POI2010 题解整理

Description

大帝拥有n个星球，因为距离非常遥远，所以大帝在他所居住的1号星球和他的军事基地霸中所在的2号星球建造了两个传送门，这样从1号星球到2号星球就只需要250分钟，回去也一样（双向）。

由于科技的发展，各个星球陆陆续续建造了和自己居民最经常去的星球之间的传送门，并且他们的传送门只需要1个小时（真快啊！），他们发现和别的星球建设传送门对促进经济发展有很大的帮助，于是向和其他所有星球建设传送门发展。

大帝突然发现两两星球的传送门的建设会威胁到他的安全，可是他又想促进自己帝国的发展，于是他请到了他精心培养的你，希望你能帮他解决这个难题。

Input

• 第一行为两个由空格隔开的整数$n(2\le n\le4*10^4)$和$m(0\le m\le 10^6)$，$n$表示星球数，$m$表示其他星球已经建造的传送门的对数（传送门都是两两建造的，但不包括大帝在1号和2号的）。
• 接下来$m$行每行两个由空格隔开的整数$x,y$$(2\le x,y\le4*10^4)$，表示这两个星球建造了传送门连接。

Sample Input

10 10
1 3
3 5
5 7
7 9
2 9
1 4
4 6
6 8
8 10
2 10

Input Details

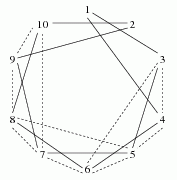
实线连接的是已经造好传送门的两星球，虚线连接表示可以增加建造的传送门两星球。

可以看出，建造了10对以后，从1号到2号星球还是大帝的1->2传送门最快。

Output

• 一个整数，表示还能让多少对传送门建造，但又不会比大帝从1号星球到2号星球快（就是说增加传送门后，从1号星球到2号星球还是大帝的传送门最快）。

Sample Output

10

---

思路转自Spy大神。

---

$Solution$：

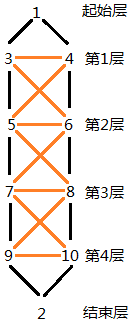
首先我们可以将原图作如下等效的变形：

$\to$ $\to$

每一层都代表着该点最短到1和2的距离。有以下结论：

• 显然除了1,2外，其他点都会被分进这4层里。那么与1相连的，到1的最短距离为2的点只能放在1,2层；与2相连的，到2的最短距离为2的点只能放在4,3层。
• 对于在某一层的点，它只能和本层与相邻层的点连线，如果跨过一层连线，就会导致1,2的最短距离不是5了。

• 其他剩余没有被扔进图里的点，将其视作第2,3层中某层的点。这样首先是不会违背题意的，而且也更优：

  • 如果扔进第1层，那么其增加的边个数是$size_1+1+size_2$。
  • 如果扔进第2层，那么其增加的边个数是$size_1+size_2+size_3$。

  显然$size_3\ge1$，所以扔进中间两层更优。

• 显然增加的数值只会跟每层实际存在的点的个数有关，故可以枚举有多少点进入2层，多少点进入3层，再计算即可。

$Code$：（基本转自Spy大神）

#include <bits/stdc++.h>
#define M 40005
using namespace std;
typedef long long ll;
inline void Rd(int &res){
    res=0;char c;
    while(c=getchar(),c<48);
    do res=(res<<3)+(res<<1)+(c^48);
    while(c=getchar(),c>47);
}
vector<int>G[M];
int id[M],cnt[6],rcnt[6];
int main(){
    int n,m;Rd(n),Rd(m);
    for(int i=1;i<=m;i++){
        int u,v;
        Rd(u),Rd(v);
        G[u].push_back(v);
        G[v].push_back(u);
    }
    memset(id,-1,sizeof(id));
    id[1]=0,id[2]=5;

    for(int j=0;j<G[1].size();j++){
        int v=G[1][j];
        id[v]=1,cnt[id[v]]++;
    }
    for(int j=0;j<G[2].size();j++){
        int v=G[2][j];
        id[v]=4;cnt[id[v]]++;
    }
    for(int i=1;i<=n;i++)
        if(id[i]==1){
            for(int j=0;j<G[i].size();j++){
                int v=G[i][j];
                if(!id[v]){
                    id[v]=2;
                    cnt[id[v]]++;
                }
            }
        }else if(id[i]==4){
            for(int j=0;j<G[i].size();j++){
                int v=G[i][j];
                if(!id[v]){
                    id[v]=3;
                    cnt[id[v]]++;
                }
            }
        }
    int Cnt=0;
    for(int i=1;i<=n;i++)Cnt+=(id[i]==-1);//没有分配到层的元素个数
//  printf("Cnt=%d\n",Cnt);
    rcnt[1]=cnt[1],rcnt[4]=cnt[4];
    int ans=0,res=rcnt[1]*(rcnt[1]-1)/2+rcnt[4]*(rcnt[4]-1)/2+1*rcnt[1]+rcnt[4]*1;
    for(int k=0;k<=Cnt;k++){
        rcnt[2]=cnt[2]+k,rcnt[3]=cnt[3]+Cnt-k;
        int tmp=rcnt[2]*(rcnt[2]-1)/2+rcnt[3]*(rcnt[3]-1)/2+
                rcnt[1]*rcnt[2]+rcnt[2]*rcnt[3]+rcnt[3]*rcnt[4];
        ans=max(tmp,ans);
    }
    cout<<ans+res-m<<endl;
}