基于Linux的C++ Part 4: 算法

4.1 算法概念与特征

算法基本概念

• 算法定义：解决问题的方法与步骤
• 设计算法的目的：给出解决问题的逻辑描述，根据算法描述进行实际编程

算法特征

• 有穷性：算法在每种情况下都可以在有限步后终止
• 确定性：算法步骤的顺序和内容没有二义性
• 输入：算法有零个或多个输入
• 输出：算法至少具有一个输出
• 有效性：所有操作具有明确含义，并能在有限时间内完成
  正确性不是算法的特征，算法的正确性需要数学证明

算法示例

• 示例一：3*3 幻方
  
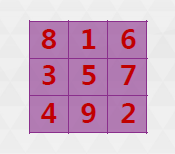
  步骤1：把 1 写在第一行中间一格
  步骤2：在该格右上方的那一格中写入下一自然数
  在此过程中，若该数已超出 3 × 3 幻方范围，则将该数书写在其所在的那一排或列的另一端格子中，即相当于认为幻方外围仍然包含了同样的幻方，而该数就写在外围幻方的同样位置
  每写完三个数，将第四个数写在第三个数下面格子中
  步骤3：重复步骤2，直到所有格子均填满
• 查英文单词
  步骤1：翻开词典任意一页
  步骤2：若所要的词汇按字母排列顺序在本页第一个单词之前，则往前翻开任意一页，重复步骤2；若所查词汇在本页最后一个单词之后，则往后翻开任意一页，重复步骤2
  步骤3：若上述两条件均不满足，则该单词要么在本页上，要么词典中不存在
  依次比较本页单词，或者查出该单词，或者得到该单词查不到的结论

4.2 算法描述

伪代码

• 混合自然语言与计算机语言、数学语言的算法描述方法
• 优点：方便，容易表达设计者思想，能够清楚描述算法流程，便于修改
• 缺点：不美观，复杂算法不容易理解
• 示例1：顺序结构
  执行某任务
  执行下一任务
• 示例2：分支结构

 if( 条件表达式 )
 	处理条件为真的情况
 else 
 	处理条件为假的情况

switch( 条件变量 ){
case 常量表达式 1: 处理分支 1
case 常量表达式 2: 处理分支 2
……
default: 处理默认分支
}

• 示例3：循环结构

for( 初始化表达式; 条件表达式; 步进表达式 ) || while( 条件表达式 )
{
循环体内部代码逻辑描述
}

流程图（程序框图）

• 使用图形表示算法执行逻辑
• 优点：美观，算法表达清晰
• 缺点：绘制复杂，不易修改，占用过多篇幅
• 常用流程图的框图与符号
  
• 示例1：幻方流程图
  
• 示例二： 查英文单词
  

4.3 算法设计与实现

算法设计与实现步骤

• 构造算法解决问题
• 按照自顶向下、逐步求精的方式进行
• 使用程序设计语言编程实现

典型示例1 ：素性判定问题

判断给定的某个自然数 n（大于 2）是否为素数
算法逻辑：

• 输入：大于 2 的正整数 n
• 输出：该数是否为素数，若为素数返回 true，否则返回 false
• 步骤 1：设除数 i 为 2
• 步骤 2：判断除数 i 是否已为 n，若为真返回 true，否则继续
• 步骤 3：判断 n % i 是否为 0，若为 0 返回 false，否则继续
• 步骤 4：将除数 i 递增，重复步骤 2

素数判定函数方法一,循环次数多，效率非常低
bool IsPrime( unsigned int n )
{
unsigned int i = 2;
while( i < n )
{
if( n % i == 0 )
return false;
i++;
}
return true;
}

素数判定函数方法二：程序快于方法一，循环的遍历的次数由n降至sqrt(n)
bool IsPrime( unsigned int n )
{
unsigned int i = 2;
while( i <= (unsigned int)sqrt(n) )//若一个自然数n为和数，则一定存在在2~n之间的两个数p和q（p<=q），且p << sqrt(n)
{
if( n % i == 0 )//如果i能被n整除，则直接返回结果，n不是素数
return false;
i++;
}
return true;
}

素数判定函数方法三：更快，结合了方法一和方法二
bool IsPrime( unsigned int n )
{
unsigned int i = 3;//从3开始循环
if( n % 2 == 0 ) //如果这个数是偶数，则一定不是素数，直接返回结果
return false;
while( i <= (unsigned int)sqrt(n) )
{
if( n % i == 0 )
return false;
i += 2;//每次递增2，因为进入while循环之前已经判断奇偶性
}
return true;
}

素数判定函数方法四，更精确
bool IsPrime( unsigned int n )
{
unsigned int i = 3;
if( n % 2 == 0 )
return false;
while( i <= (unsigned int)sqrt(n) + 1 )//sqrt(n)保存的是浮点型，会有微小误差，会漏掉一些平方数
{
if( n % i == 0 )
return false;
i += 2;
}
return true;
}

素数判定函数方法五，更精确 更快
bool IsPrime( unsigned int n )
{
unsigned int i = 3, t = (unsigned int)sqrt(n) + 1;//只计算一次sqrt(n)，程序就会变快，因为这里n不变。
if( n % 2 == 0 )
return false;
while( i <= t )
{
if( n % i == 0 )
return false;
i += 2;
}
return true;
}

算法选择

• 算法选择的权衡指标
  正确性：算法是否完全正确？
  效率：在某些场合，对程序效率的追求具有重要意义
  可理解性：算法是否容易理解，也是必须要考虑的
• 算法评估：
  衡量算法的好坏，主要是效率

典型示例2 ：最大公约数问题

求两个正整数 x 与 y 的最大公约数
函数原型设计

unsigned int gcd( unsigned int x, unsigned int y );

最大公约数函数：穷举法 效率低
unsigned int gcd( unsigned int x, unsigned int y )
{
unsigned int t;
t = x < y ? x : y;
while( x % t != 0 || y % t != 0 )
t--;
return t;
}

最大公约数函数：欧氏算法*/
输入：正整数 x、y
输出：最大公约数
步骤 1：x 整除以 y，记余数为 r
步骤 2：若 r 为 0，则最大公约数即为 y，算法结束
步骤 3：否则将 y 作为新 x，将 r 作为新 y，重复上述步骤
unsigned int gcd( unsigned int x, unsigned int y )
{
unsigned int r;
while( true )
{
r = x % y;
if( r == 0 )
return y;
x = y;
y = r;
}
}

4.4 递归算法

递归问题

递归问题的引入

• 递推公式：数学上非常常见
  例一：阶乘函数：1! = 1，n! = n × (n-1)!
  例二：斐波那契数列函数：f(1) = f(2) = 1，f(n) = f(n-1) + f(n-2)
• 递推函数一定是分段函数，具有初始表达式
• 递推函数的计算逻辑：逐步简化问题规模

递归的工作步骤

• 递推过程：逐步分解问题，使其更简单
• 回归过程：根据简单情形组装最后的答案

阶乘函数示例

使用循环实现
unsigned int GetFactorial( unsigned int n )
{
unsigned int result = 1, i = 0;
while( ++i <= n )
result *= i;
return result;
}

使用递归实现
unsigned int GetFactorial( unsigned int n )
{
unsigned int result;
if( n == 1 ) result = 1;
else result = n * GetFactorial( n - 1 );
return result;
}

斐波那契数列函数示例

使用循环实现
unsigned int GetFibonacci( unsigned int n )
{
unsigned int i, f1, f2, f3;
if( n == 2 || n == 1 ) return 1;
f2 = 1; f1 = 1;
for( i = 3; i <= n; i++ ){
f3 = f1 + f2; f1 = f2; f2 = f3;
}
return f3;
}

使用递归实现
unsigned int GetFibonacci( unsigned int n )
{
if( n == 2 || n == 1 ) return 1;
else return GetFibonacci( n - 1 ) + GetFibonacci( n - 2 );
}

循环与递归的比较

• 循环使用显式的循环结构重复执行代码段，递归使用重复的函数调用执行代码段
• 循环在满足其终止条件时终止执行，而递归则在问题简化到最简单情形时终止执行
• 循环的重复是在当前迭代执行结束时进行，递归的重复则是在遇到对同名函数的调用时进行
• 循环和递归都可能隐藏程序错误，循环的条件测试可能永远为真，递归可能永远退化不到最简单情形
• 理论上，任何递归程序都可以使用循环迭代的方法解决
  递归函数的码更短小精悍
  一旦掌握递归的思考方法，递归程序更易理解

递归函数调用的栈框架

#include <iostream>
using namespace std;
void PrintWelcomeInfo();
unsigned int GetInteger();
unsigned int GetFactorial( unsigned int n );
int main()
{
unsigned int n, result;
PrintWelcomeInfo();
n = GetInteger();
result = GetFactorial( n );
cout << n << "! = " << result << ".\n";
return 0;
}
void PrintWelcomeInfo()
{
cout << "The program gets a number and computes the factorial.\n";
}
unsigned int GetInteger()
{
unsigned int t;
cout << "Input a non-negative number: ";
cin >> t;
return t;
}
unsigned int GetFactorial( unsigned int n )
{
unsigned int result;
if( n == 0 )
result = 1;
else
result = n * GetFactorial( n - 1 );
return result;
}

• 函数调用栈框架说明
  

汉诺塔问题

假设有三个分别命名为 X、Y 和 Z 的塔座，在塔座 X 上插有 n 个直径大小不同、从小到大分别编号为 1, 2, …, n 的圆盘，如图所示：

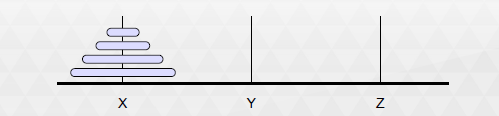
要求将塔座X上的 n 个圆盘移动到塔座 Z 上并按相同顺序叠放，圆盘移动时必须遵循下述规则：

• 每次只能移动一个圆盘；
• 圆盘可以插在X、Y与Z中的任意塔座上；
• 任何时刻都不能将较大的圆盘压在较小的圆盘上。

如何实现移动圆盘的操作呢？
问题分析
待解决的问题

• Q1：是否存在某种简单情形，问题很容易解决
• Q2：是否可将原始问题分解成性质相同但规模较小的子问题，且新问题的解
  答对原始问题有关键意义

解决思维

• A1：只有一个圆盘时是最简单情形
• A2：对于 n > 1，考虑 n – 1 个圆盘，如果能将 n - 1 个圆盘移动到某个塔
  座上，则可以移动第 n 个圆盘
  策略：首先将 n – 1 个圆盘移动到塔座 Y 上，然后将第 n 个圆盘移动到 Z 上，
  最后再将 n - 1 个圆盘从 Y 上移动到 Z 上

伪代码

void MoveHanoi( unsigned int n, HANOI from, HANOI tmp, HANOI to )
{
if( n == 1 )
将一个圆盘从 from 移动到 to
else
{
将 n – 1 个圆盘从 X 以 Z 为中转移动到 Y
将圆盘 n 从 X 移动到 Z
将 n - 1个圆盘从 Y 以 X 为中转移动到 Z
}
}

程序代码

#include <iostream>
using namespace std;
void Welcome();
int GetPlate();
void MoveHanoi(int n,char from,char tmp,char to);
void MovePlate(int n, char from, char to);
int main() {
	int plates;
	int sum=0;
	Welcome();
	plates = GetPlate();
	cout << "Move process: \n";
	MoveHanoi(plates, 'X', 'Y', 'Z');
	cout << "Finish!\n";
	return 0;
}

void Welcome() {
	cout << "This is a Tower of Hanoi problem!" << endl;
}

int GetPlate() {
	int n;
	cout << "Please input the counts of the plates: " << endl;
	cin >> n;
	cout << "You want to move " << n << " plates.\n";
	return n;
}

void MovePlate(int n, char from, char to) {
	cout << "No" << n << ": " << from << "  -  " << to << endl;
}

void MoveHanoi(int n, char from, char tmp, char to){
	if (n == 1) {
		MovePlate(1, from, to);
	}
	else {
		MoveHanoi(n - 1, from, to, tmp);
		MovePlate(n, from, to);
		MoveHanoi(n - 1, tmp, from, to);
	}
}

运行结果：
This is a Tower of Hanoi problem!
Please input the counts of the plates:
4
You want to move 4 plates.
Move process:
No1: X  -  Y
No2: X  -  Z
No1: Y  -  Z
No3: X  -  Y
No1: Z  -  X
No2: Z  -  Y
No1: X  -  Y
No4: X  -  Z
No1: Y  -  Z
No2: Y  -  X
No1: Z  -  X
No3: Y  -  Z
No1: X  -  Y
No2: X  -  Z
No1: Y  -  Z
Finish!

递归信任

• 递归实现是否检查了最简单情形
  在尝试将问题分解成子问题前，首先应检查问题是否已足够简单
  在大多数情况下，递归函数以 if 开头
  如果程序不是这样，仔细检查源程序
• 大量递归错误是由没有正确解决最简单情形导致的
  最简单情形不能调用递归
• 递归分解是否使问题更简单
  只有分解出的子问题更简单，递归才能正确工作，否则将形成无限递
  归，算法无法终止
• 问题简化过程是否能够确实回归最简单情形，还是遗漏了某些情况
  如汉诺塔问题需要调用两次递归过程，程序中如果遗漏了任意一个都
  会导致错误
• 子问题是否与原始问题完全一致
  如果递归过程改变了问题实质，则整个过程肯定会得到错误结果
• 使用递归信任时，子问题的解是否正确组装为原始问题的解
  将子问题的解正确组装以形成原始问题的解也是必不可少的步骤

4.5 容错与算法复杂度

容 错

• 容错的定义：允许错误的发生
• 错误的处理
  很少见的特殊情况或普通错误：忽略该错误不对程序运行结果产生影响
  用户输入错误：通知用户错误性质，提醒用户更正输入
  致命错误：通知用户错误的性质，停止执行
• 典型容错手段
  数据有效性检查
  程序流程的提前终止
• 数据有效性检查

void GetUserInput()
{
获取用户输入数据
while( 用户输入数据无效 )
{
通知用户输入数据有误，提醒用户重新输入数据
重新获取用户输入数据
}
}
void Input()
{
GetInputData();
while( !IsValid() )
{
OutputErrorInfo();
GetinputData();
}
}

• 程序流程的提前终止

const int failed_in_testing_primality = 1;
bool IsPrime( unsigned int n )
{
unsigned int i = 3, t = (unsigned int)sqrt(n) + 1;
if( n <= 1 )
{
cout << "IsPrime: Failed in testing the primality of " << n << endl;
exit( failed_in_testing_primality )//在"stdlib.h"定义的
}
if( n == 2 )
return true;
if( n % 2 == 0 )
return false;
while( i <= t )
{
if( n % i == 0 )
return false;
i += 2;
}
return true;
}

算法复杂度

• 引入算法复杂度的目的
  度量算法的效率与性能
• 大 O 表达式
  算法效率与性能的近似表示（定性描述）
  算法执行时间与问题规模的关系
• 表示原则
  忽略所有对变化趋势影响较小的项，例如多项式忽略高阶项之外的所有项
  忽略所有与问题规模无关的常数，例如多项式的系数
• 标准算法复杂度类型
  O(1)：常数级，表示算法执行时间与问题规模无关
  O(log(n))：对数级，表示算法执行时间与问题规模的对数成正比
  O(sqrt(n))：平方根级，表示算法执行时间与问题规模的平方根成正比
  O(n)：线性级，表示算法执行时间与问题规模成正比
  O(nlog(n))：nlog(n) 级，表示算法执行时间与问题规模的 n*log(n) 成正比
  O(n2)：平方级，表示算法执行时间与问题规模的平方成正比
  ……
• 算法复杂度估计
  以嵌套的循环次数估计：

for( i = 0; i < n; i++ )
	cout << "No. " << I << ": Hello, World!\n";					//O(n)

for( i = 0; i < n; i++ )
	for( j = 0; j < n; j++ )
		cout << "Hello, World!\n";								//O(n2)

for( i = 0; i < n; i++ )
	for( j = i; j < n; j++ )
		cout << "Hello, World!\n";								//O(n2)

4.6 编程实战

• 设计算法，将某个大于1的自然数n分解为其素因子的乘积，如6=23，7=7，8=22*2。

#include <iostream>
#include "stdlib.h"
using namespace std;
const int failed_in_input=1;
void Welcome();
int GetInteger();
void Decompose(int n);
int main(){
    int n;
    n=GetInteger();
    Decompose(n);
    cout << "Finish!\n";
    return 0;
}

void Welcome(){
    cout << "This is a program to decompose a natural number!\n";
}

int GetInteger(){
    int n;
    cout <<"Please enter a number !\n";
    cin >> n; 
    if (n<=1){
        cout << "Failed in decomposing because of your invalid input!!\n";
        exit(failed_in_input);
    }
    return n;
}

void Decompose(int n){
    int i=2;							/循环标志
    cout << n << "= ";
    if(n==2){
        cout << 1 << " * " << 2 << endl;
    }
    else{
        for(i=2;i<=n;i++){				//从最小的质数 2  开始执行循环
        	while (n!=i)				//停止条件
        	{
            	if (n%i==0){			//判断当前i是否能整除n,若能 求商 ，继续
                	cout << i << "*" ;
                	n = (n/i);			//把商赋值给n，继续,直到n<i，跳出
            	}
            	else{
                	break;				//判断当前i是否能整除n,若不能，则i+1
            	}
        	}  
    	} 
    	cout << n << endl;
    }
    
}

运行结果：
Please enter a number !
1
Failed in decomposing because of your invalid input!!

Please enter a number !
2
2= 1 * 2
Finish!

Please enter a number !
8
8= 2*2*2

Please enter a number !
11
11= 11
Finish!

• 设计算法，分别使用循环和递归两种策略求二项式系数C(n,k)。其中，n为自然数，k为不大于n的非负整数。