【主成分分析】详解常用的降维方法-主成分分析（PCA）算法

程序遇上智能星空

已于 2022-06-10 16:41:34 修改

阅读量9.4k

点赞数 8

分类专栏：深入浅出讲解自然语言处理机器学习文章标签：算法机器学习深度学习线性代数

于 2022-06-10 16:33:32 首次发布

本文链接：https://blog.csdn.net/kevinjin2011/article/details/125223420

版权

深入浅出讲解自然语言处理同时被 2 个专栏收录

27 篇文章 640 订阅

订阅专栏

机器学习

12 篇文章 18 订阅

订阅专栏

本文收录于《深入浅出讲解自然语言处理》专栏，此专栏聚焦于自然语言处理领域的各大经典算法，将持续更新，欢迎大家订阅！
个人主页：有梦想的程序星空
个人介绍：小编是人工智能领域硕士，全栈工程师，深耕Flask后端开发、数据挖掘、NLP、Android开发、自动化等领域，有较丰富的软件系统、人工智能算法服务的研究和开发经验。
如果文章对你有帮助，欢迎关注、点赞、收藏、订阅。

1、序言

我们在研究某些问题时，需要处理带有很多变量的数据，比如研究房价的影响因素，需要考虑的变量有物价水平、土地价格、利率、就业率、城市化率等。变量和数据很多，但是可能存在噪音和冗余，因为这些变量中有些是相关的，那么就可以从相关的变量中选择一个，或者将几个变量综合为一个变量，作为代表。用少数变量来代表所有的变量，用来解释所要研究的问题，就能从化繁为简，抓住关键，这也就是降维的思想。

在特征提取与处理时，涉及高维特征向量的问题往往容易陷入维度灾难。随着数据集维度的增加，算法学习需要的样本数量呈现指数级增加。有些应用中，遇到这样的大数据是非常不利的，而且从大数据集中学习需要更多的内存和处理能力。另外，随着维度的增加，数据的稀疏性会越来越高，在高维向量空间中探索数据集比在同样稀疏的数据集中探索更加困难。

2、PCA简介

主成分分析（Principal Components Analysis，简称PCA）是由Hotelling于1933年首先提出的。由于多个维度变量之间往往存在着一定程度的相关性，自然希望通过线性组合的方式，从这些指标中尽可能快地提取信息。主成分分析适用于原有维度变量之间存在较高程度相关的情况。在主成分分析适用的场合，一般可以用较少的主成分得到较多的信息量，从而得到一个更低维的向量。通过主成分既可以降低数据“维数”又保留了原数据的大部分信息。

主成分分析法就是一种运用线性代数的知识来进行数据降维的方法，它将多个变量转换为少数几个不相关的综合变量来比较全面地反映整个数据集。这是因为数据集中的原始变量之间存在一定的相关关系，可用较少的综合变量来综合各原始变量之间的信息。这些综合变量称为主成分，各主成分之间彼此不相关，即所代表的信息不重叠。

主成分分析（PCA）是一种常用的无监督学习方法，利用正交变换把由线性相关变量表示的观测数据转换为几个由线性无关变量表示的数据。线性无关的变量称为主成分。主成分的个数通常小于原始变量的个数，所以PCA是一种降维算法。

主成分分析算法（PCA）是最常用的线性降维方法，它的目标是通过某种线性投影，将高维的数据映射到低维的空间中，并期望在所投影的维度上数据的信息量最大（方差最大），以此使用较少的数据维度，同时保留住较多的原数据点的特性。

3、数学知识

给定一个样本 $X = \{ {X_1},{X_2}, \cdots ,{X_n}\}$ ，

则其均值为：

$\bar X = \frac{{\sum\limits_{i = 1}^n {{X_i}} }}{n}$

标准差为：

上述的标准差、方差都是针对单变量（一维），然而生活中的大多数数据都是二维以上，我们需要去衡量这些维度之间的关系，这时就需要用到协方差。

对于单变量 $X$ 的方差，也可以写成如下形式：

${\mathop{\rm var}} (X) = \frac{{\sum\limits_{i = 1}^n {({X_i} - \bar X)({X_i} - \bar X)} }}{{n - 1}}$

那么，对于两个变量（维度）之间的协方差，也可以写成类似形式：

${\mathop{\rm cov}} (X,Y) = \frac{{\sum\limits_{i = 1}^n {({X_i} - \bar X)({Y_i} - \bar Y)} }}{{n - 1}}$

协方差矩阵中的每个元素都是两个变量之间的协方差。如：在3维情况下，以x、y、z来表示这三个维度，则组成的协方差矩阵如下：

$C = \left( {\begin{array}{*{20}{c}} {{\mathop{\rm cov}} (x,x)}&{{\mathop{\rm cov}} (x,y)}&{{\mathop{\rm cov}} (x,z)}\\ {{\mathop{\rm cov}} (y,x)}&{{\mathop{\rm cov}} (y,y)}&{{\mathop{\rm cov}} (y,z)}\\ {{\mathop{\rm cov}} (z,x)}&{{\mathop{\rm cov}} (z,y)}&{{\mathop{\rm cov}} (z,z)} \end{array}} \right)$

4、PCA步骤

输入样本集 $X = \{ {X_1},{X_2}, \cdots ,{X_n}\}$ ，和指定的主成分个数 $p'$ ，主成分可以按以下步骤计算得出：

（1）先对数据进行去中心化（如Z-score标准化）的规范处理，每个变量减去各自的均值，这样可以将数据的中心归到零点位置，即均值为零。

（2）计算中心化后的样本 $X$ 的协方差矩阵：

$C = \frac{{X{X^T}}}{{n - 1}}$

（3）计算协方差矩阵 $C$ 的特征值，并按从大到小的顺序排列，记为：

${\lambda _1} \ge {\lambda _2} \ge \cdots \ge {\lambda _p}$

（4）计算特征值对应的特征向量，取前 $p'$ 个特征值对应的特征向量构成投影矩阵：

$W = \{ {w_1},{w_2}, \cdots ,{w_{p'}}\}$

（5）将数据转换到上述投影矩阵构建的新空间中，从而达到降维的目的。

5、主成分贡献率

降维后低维空间的维数 $p'$ 通常由用户事先指定，不过不同的 $p'$ 对降维效果有很大的影响，如何靠谱地确定 $p'$ ?

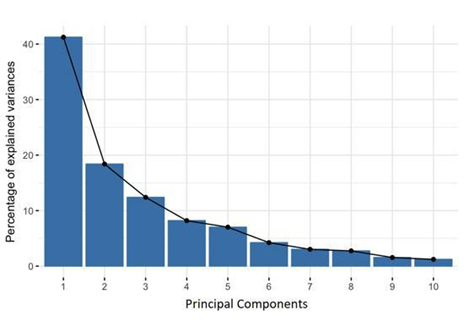
通常有两种方式：根据大于1的特征值的个数确定主成分的个数，如 $p = 10,{\lambda _1} > {\lambda _2} > \cdots > {\lambda _6} > 1$ ，那么 $p' = 6$ ；根据主成分的累计贡献率确定主成分的个数，使累计贡献率>85%或者其他值。对于第 $k$ 个主成分，其对方差的贡献率为：

$\frac{{{\lambda _k}}}{{\sum\limits_{i = 1}^p {{\lambda _i}} }}$

前 $k$ 个主成分贡献率的累计值称为累计贡献率：

$p' = \mathop {\arg \min }\limits_k \frac{{\sum\limits_{i = 1}^k {{\lambda _k}} }}{{\sum\limits_{i = 1}^p {{\lambda _i}} }} > 85\%$

6、python实现

sklearn实现：

class sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False, svd_solver=’auto’, tol=0.0, iterated_power=’auto’, random_state=None)

其主要包含3个参数：

（1）n_components确定要保留的主成分个数，类型为int 或者 string，缺省时默认为None，即所有成分被保留。赋值为int，比如n_components=1，将把原始数据降到一个维度。赋值为string，比如n_components=’mle’，将自动选取特征个数n，使得满足所要求的方差百分比。

（2）copy表示是否在运行算法时，将原始训练数据复制一份。若为True，则运行PCA算法后，原始训练数据的值不会有任何改变，因为是在原始数据的副本上进行运算；若为False，则运行PCA算法后，原始训练数据的值会改，因为是在原始数据上进行降维计算。

（3）whiten表示白化，即使得每个特征具有相同的方差，缺省时默认为False。

# -*- coding: utf-8 -*-

from sklearn.decomposition import PCA
import numpy as np

data = np.array([[1,1],[1.5,1.6],[2,2],[2.4,2.4],[1.95,1.9],[3,3],[3.3,3.1]])

pca = PCA(n_components=1)
newdata = pca.fit_transform(data)

print "原始数据-二维:", data
print "降维后数据-一维:", newdata

7、问题

为什么样本要在“协方差矩阵C的最大K个特征值所对应的特征向量”上进行投影？

PCA降维的目的就是为了在尽量保证“信息量不丢失”的情况下，对原始特征进行降维，也就是尽可能将原始特征往具有最大信息量的维度上进行投影。根据最大方差理论：方差越大，信息量就越大。协方差矩阵的每一个特征向量就是一个投影面，每一个特征向量所对应的特征值就是原始特征投影到这个投影面之后的方差。由于投影过去之后，我们要尽可能保证信息不丢失，所以要选择具有较大方差的投影面对原始特征进行投影，也就是选择具有较大特征值的特征向量。然后将原始特征投影在这些特征向量上，投影后的值就是新的特征值，并且使降维后信息量损失最小。

8、优缺点

优点：

以方差衡量信息的无监督学习，不受样本标签限制。
由于协方差矩阵对称，因此k个特征向量之间两两正交，也就是各主成分之间正交，正交就肯定线性不相关，可消除原始数据成分间的相互影响。
可减少指标选择的工作量，而且计算方法简单，易于在计算机上实现。

缺点：

主成分解释其含义往往具有一定的模糊性，不如原始样本完整。
贡献率小的主成分往往可能含有对样本差异的重要信息，也就是可能对于区分样本的类别（标签）更有用。

关注微信公众号【有梦想的程序星空】，了解软件系统和人工智能算法领域的前沿知识，让我们一起学习、一起进步吧！

程序遇上智能星空

关注

8
点赞
踩
64

收藏

觉得还不错? 一键收藏
打赏
4
评论
【主成分分析】详解常用的降维方法-主成分分析（PCA）算法

主成分分析（PCA）是一种常用的无监督学习方法，利用正交变换把由线性相关变量表示的观测数据转换为几个由线性无关变量表示的数据。线性无关的变量称为主成分。主成分的个数通常小于原始变量的个数，所以PCA是一种降维算法。主成分分析算法（PCA）是最常用的线性降维方法，它的目标是通过某种线性投影，将高维的数据映射到低维的空间中，并期望在所投影的维度上数据的信息量最大（方差最大），以此使用较少的数据维度，同时保留住较多的原数据点的特性。.........
复制链接

扫一扫