运筹系列66：tsp问题求解器concorde介绍

IE06

已于 2023-09-06 21:25:22 修改

阅读量3.1k

点赞数 1

分类专栏：运筹学文章标签： julia

于 2023-02-27 22:40:58 首次发布

本文链接：https://blog.csdn.net/kittyzc/article/details/128995730

版权

运筹学专栏收录该内容

93 篇文章

订阅专栏

Concorde是一个用纯C编写的解决对称TSP问题的工具，最大处理过85900个城市。它利用线性规划求解器QSopt进行边界优化。文章介绍了分枝定界法的原理，列生成和行生成方法，以及如何在Julia环境中使用Concorde。此外，还提供了Mac应用的使用方法和编译、调试代码的步骤。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1. 简介

纯C语言编译，用于对称TSP问题求解。目前最大的应用案例为85900个城市。Concorde支持使用QSopt线性规划求解器获得bound。

1.1 求解算法简介

TSP问题模型如下，第二个约束条件是为了去除环，称为connect cut：
在这里插入图片描述
使用分枝定界法进行求解的原理如下：
首先将整数约束和去除环约束进行松弛，得到lp问题。

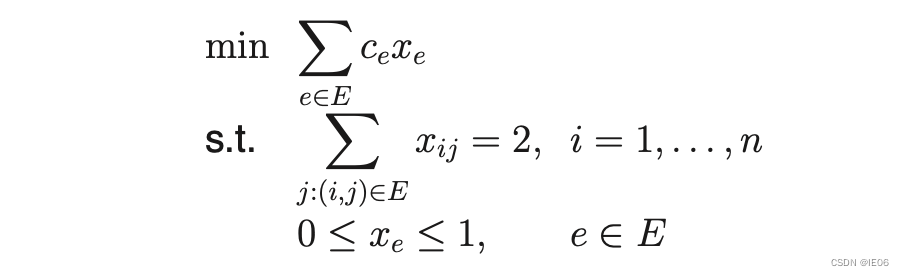
我们使用列生产方法来求解这个问题，令E‘是E的子集，比如说只允许最近的一些点参与组环。
在这里插入图片描述
获得的最优解x‘是原LP问题的可行解。我们通过对偶问题来寻找需要添加进来的变量：

对偶问题为：

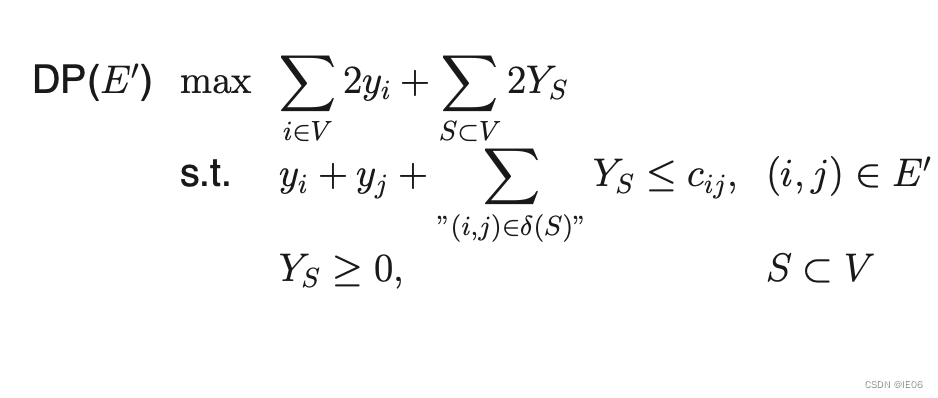
同时我们还需要用行生成法添加防止子环的约束条件。举例如下，为如图的边添加comb约束：

其他常用的cuts包括：
*

Blossom (Padberg and Rao 1982)
Path inequalities (Naddef and Rinaldi 1998)
2-handled clique tree (Padberg and Rinaldi 1991)
Star inequalities (Fleischmann 1988)

在这里插入图片描述

1.2 添加cut的例子

在这里插入图片描述
第一步，求解LP松弛问题，使用行生成不断去除环

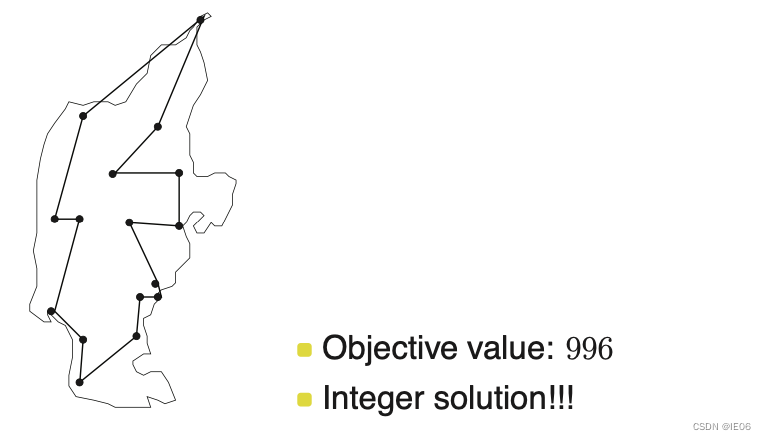
2. 使用方法

2.1 julia

Julia使用方法：

using Concorde
M = [
     0  16   7  14
    16   0   3   5
     7   3   0  16
    14   5  16   0 
]
opt_tour, opt_len = solve_tsp(M)

或者

using Concorde
n_nodes = 10
x = rand(n_nodes) .* 10000
y = rand(n_nodes) .* 10000
opt_tour, opt_len = solve_tsp(x, y; dist="EUC_2D")

或者

opt_tour, opt_len = solve_tsp("gr17.tsp")

2.2 mac应用

在应用商店中搜索concorde TSP即可，安装完成后，主界面如下：
在这里插入图片描述

使用方法：点击exact solver，然后点击下面的load按钮，加载位置文件（每行两个浮点数），返回后，点击下方的run即可，结果如下图：
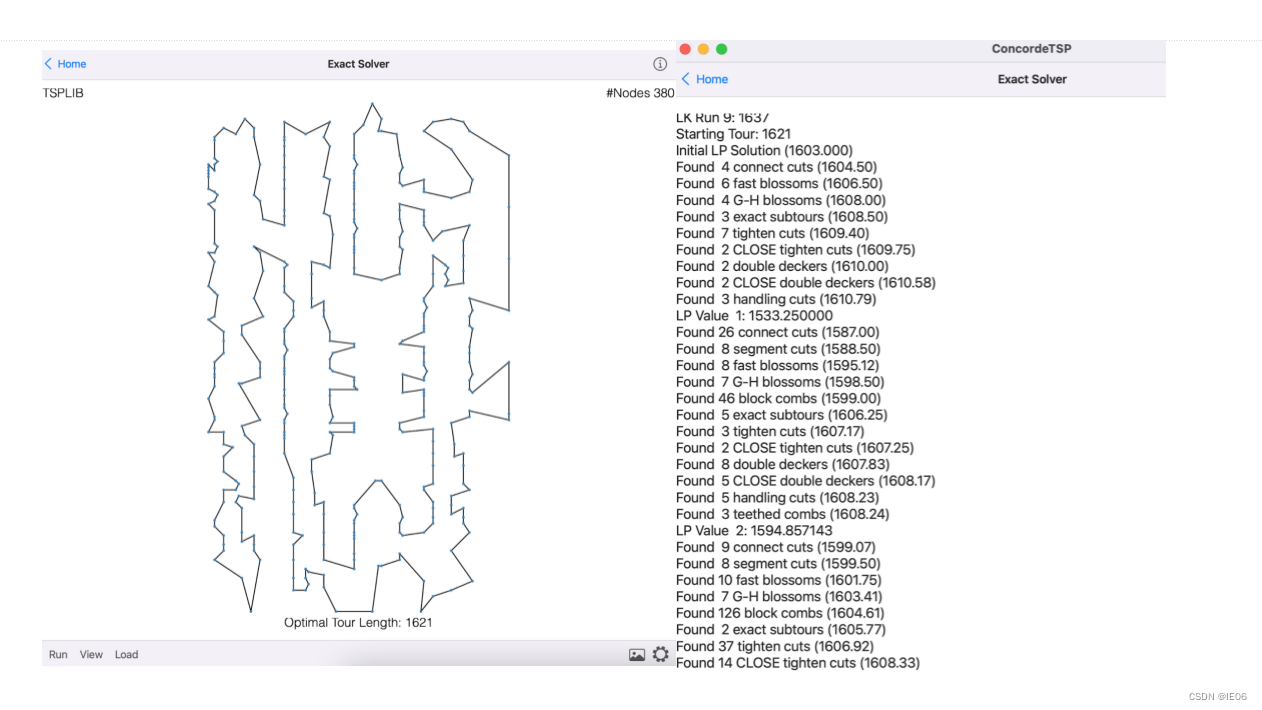
在这里插入图片描述

3. 代码分析

3.1 编译

文件夹结构如下，编译代码：

$ ./configure  --host=avr --with-qsopt=DIR #--with-cplex=DIR
$ make

程序编译生成静态库文件concorde.a，头文件concorde.h，以及一些可执行文件：

 TSP/concorde      the TSP solver
 LINKERN/linkern   the Lin-Kernighan TSP heuristic
 EDGEGEN/edgegen   generates edge sets
 FMATCH/fmatch     solves fractional 2-matching problems

例如concorde程序在TSP文件夹下：
在这里插入图片描述
测试：

$ ./concorde -s 99 -k 100
Current process id: 75398
Using random seed 99
Random 100 point set
XSet initial upperbound to 780 (from tour)
  LP Value  1: 738.500000  (0.00 seconds)
  LP Value  2: 765.000000  (0.01 seconds)
  LP Value  3: 774.660000  (0.04 seconds)
  LP Value  4: 778.000000  (0.06 seconds)
  LP Value  5: 778.465517  (0.09 seconds)
  LP Value  6: 778.705882  (0.12 seconds)
  LP Value  7: 779.538462  (0.15 seconds)
  LP Value  8: 779.937500  (0.19 seconds)
  LP Value  9: 780.000000  (0.20 seconds)
New lower bound: 780.000000
Final lower bound 780.000000, upper bound 780.000000
Exact lower bound: 780.000000
DIFF: 0.000000
Final LP has 180 rows, 336 columns, 2921 nonzeros
Optimal Solution: 780.00
Number of bbnodes: 1
Total Running Time: 0.26 (seconds)

可用参数说明：

Usage: ./concorde [-see below-] [dat_file]
   -B    do not branch
   -C #  maximum chunk size in localcuts (default 16)
   -d    use dfs branching instead of bfs
   -D f  edgegen file for initial edge set
   -e f  initial edge file
   -E f  full edge file (must contain initial edge set)
   -f    write optimal tour as edge file (default is tour file)
   -F f  read extra cuts from file
   -g h  be a grunt for boss h
   -h    be a boss for the branching
   -i    just solve the blossom polytope
   -I    just solve the subtour polytope
   -J #  number of tentative branches
   -k #  number of nodes for random problem
   -K h  use cut server h
   -M f  master file
   -m    use multiple passes of cutting loop
   -n s  problem location (just a name or host:name, not a file name)
   -o f  output file name (for optimal tour)
   -P f  cutpool file
   -q    do not cut the root lp
   -r #  use #x# grid for random points, no dups if #<0
   -R f  restart file
   -s #  random seed
   -S f  problem file
   -t f  tour file (in node node node format)
   -u v  initial upperbound
   -U    do not permit branching on subtour inequalities
   -v    verbose (turn on lots of messages)
   -V    just run fast cuts
   -w    just subtours and trivial blossoms
   -x    delete files on completion (sav pul mas)
   -X f  write the last root fractional solution to f
   -y    use simple cutting and branching in DFS
   -z #  dump the #-lowest reduced cost edges to file xxx.rcn
   -N #  norm (must specify if dat file is not a TSPLIB file)
         0=MAX, 1=L1, 2=L2, 3=3D, 4=USER, 5=ATT, 6=GEO, 7=MATRIX,
         8=DSJRAND, 9=CRYSTAL, 10=SPARSE, 11-15=RH-norm 1-5, 16=TOROIDAL
         17=GEOM, 18=JOHNSON

3.2 代码调试分析

编译完了之后，在vs中打开concorde.c，然后新建launch.json，主要修改program和args：
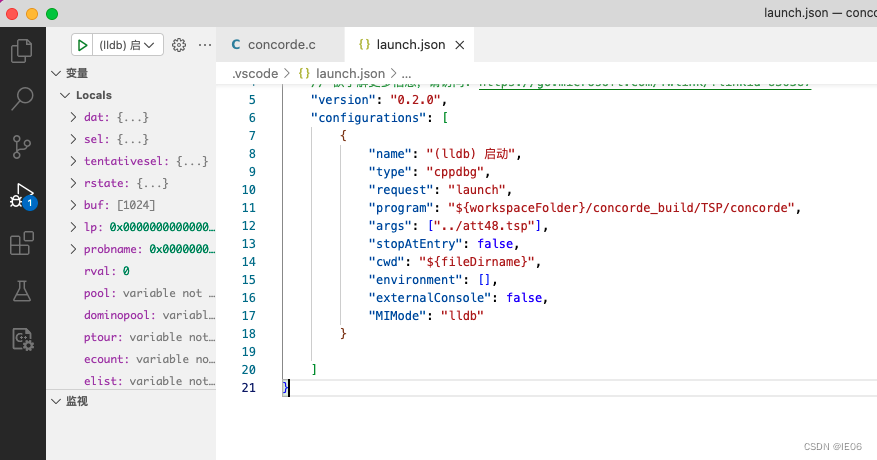
在这里插入图片描述

3.2.1 读取数据

读取命令行参数后，会配置如下参数：
在这里插入图片描述
这些函数在control.c中：

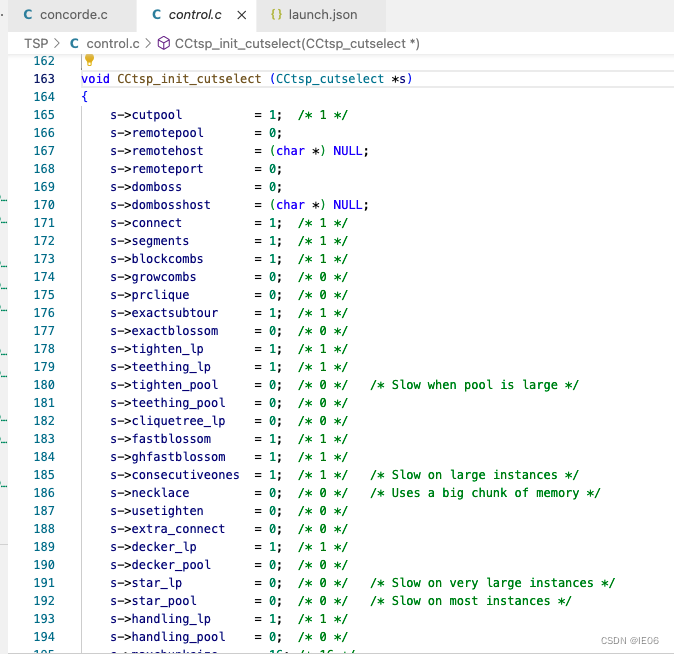
然后在getdata.c中读取tsp数据：

并打印tsp读取后的配置：

3.2.2 获取初始ub

调用findtour函数，获得一个ub。findtour函数又调用CClinkern_tour函数获得一个初始解。linkern算法可以参考之前的文章。
在这里插入图片描述

3.2.3 获取初始lb

调用build_edges或者build_fulledges函数，获取可行边集合，然后使用CCtsp_init_cutpool初始化cut集合。
CCtsp_generate_edges方法用于构造边集合，选取len(i,j) - pi[i] - pi[j]<0的边进入集合。伺候会从10条LK构造的解中添加边进入集合。
使用CCfmatch_fractional_2match方法找到最优解。

besttour初始化为1～n，CCtsp_bfs_restart开启广度搜索。
CCtsp_cutting_loop迭代求解lp问题。具体可参见tsp_lp.c。然后用x_heuristic构造新的路径。所谓x_heuristic，就是将可行边按照x轴进行排序，然后依次访问。如果调用的是CCtsp_x_greedy_tour_lk，则在之后再用lk进行一次优化。