颜色迁移是计算机视觉领域的一个很有趣的问题,它实际上要我们解决这么一个问题:基于图像A和图像B,合成一幅新的图像C,使其同时具有A的颜色和B的形状等遗传信息,即图像B在不改变它自身所表达的形状信息的情况下,学习了图像A的整体颜色基调,我们把这个过程称为图像的颜色迁移合成。其中图像A 称为颜色图像(源图像),图像B 称为形状图像(目的图像)。
在进行各种算法分析总结前,做好准备工作是必须的。先来总结下颜色迁移的必要基础知识——色彩空间及色彩空间的转换。
色彩空间
色彩空间是进行颜色信息研究的理论基础,它将颜色从人们的主观感受量化为具体的表达,为用计算机来记录和表现颜色提供了有力的依据。
一幅图像可以用不同的色彩空间表示,其视觉效果是相同的。但色彩空间的选取对图像的色彩迁移算法是否有效有很大的影响,选择一个合适的色彩空间能够保证色彩迁移结果的准确性。用于彩色图像处理的色彩空间必须同时具有独立性和均匀性。独立性是指色彩空间的三个分量互不影响,对其中某个分量的处理不会导致其它分量相对于人眼感觉发生变化;均匀性是指对色彩空间的每一个分量来说,相同数量的变化能够产生大约相同视觉重要性的变化。
色彩空间的表达形式是多样的,不同的色彩空间具有不同的特性,但因为不同的色彩空间是同构的,所以它们之间可以互相转换。
目前已发展的色彩空间非常多,如RGB,CIE XYZ,LMS,HSV,YCrCb,HSL,CMY(K),YUV,lαβ等。
下面主要介绍RGB色彩空间和lαβ色彩空间以及它们之间的转换。
RGB色彩空间
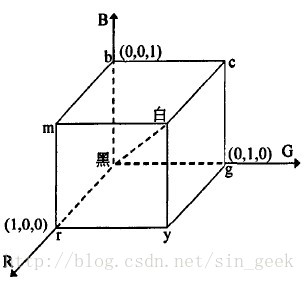
色彩混合的基本定律表明:自然界任何一种色彩均可用红、绿、蓝三种原色光混合产生,这在几何上能够以R、G、B三个互相垂直的轴所构成的空间坐标系统来表示,称为RGB色彩空间。如图1所示,RGB色系坐标中三维空间的三个轴分别于红、绿、蓝三基色相对应,原点对应黑色,离原点最远的顶点对应白色,而立方体内其余各点对应不同的颜色。RGB色彩系统用R、G、B三原色通过不同比例的混合来表示任一种色彩,因而它不能直观地度量色调、饱和度和亮度。而且,各分量之间存在着一定的相关性,它们在大多数情况下都是成正比的,主要表现为自然场景中若某一通道大,则像素的其他通道值也较大。这意味着,如果要对图像的色彩进行处理,常常需要对像素的三个分量同时进行修改才不会影响图像的真实感,这将大大增加颜色调整过程的复杂性。因此,在RGB色彩空间下进行色彩迁移会比较复杂,得到的视觉效果也不自然。
图1 RGB颜色空间
另外,RGB是与设备相关的色彩空间,即:不同的扫描仪扫描同一幅图像,会得到不同色彩的图像数据;不同型号的显示器显示同一幅图像,也会有不同的色彩显示结果。
lαβ色彩空间
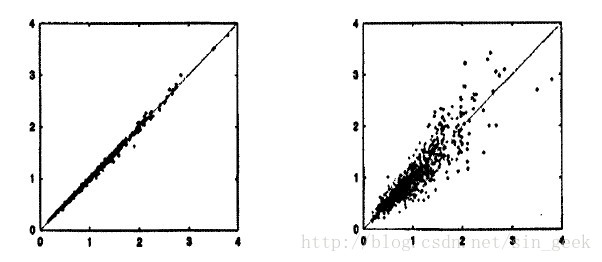
lαβ色彩空间是在LMS空间的基础上建立起来的。LMS空间三通道间的相关性很大。图2是Ruderman等人在一幅用LMS空间表示的图像中随机抽取1000个像素点生成的坐标关系图。从图中可以看出,L、M、S三个通道有很大的相关性,尤其是L与M之间。
图2 LMS色彩空间中L-M和L-S分布图
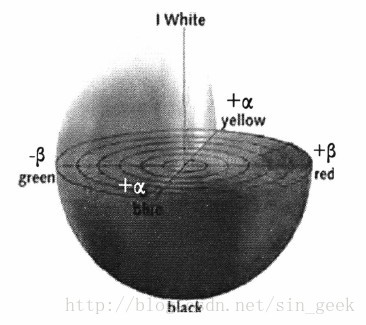
Buchsbaum等人对色彩迁移进行了研究,利用一些正交线性变换将人类视觉系统所能感受到的红、绿、蓝三色信号变换到三个不相关的色彩分量。在他们的研究基础上,Ruderman等人经过对大量的自然界图像进行颜色分布统计,得到了图像的颜色分布统计结果,并用转化色彩空间的方法形成一个统计意义上具有近似正交基的均匀色彩空间lαβ,并给出了简单的3×3矩阵运算实现RGB到lαβ空间的转化。lαβ色彩空间是基于数据驱动对人类感觉的研究,它假设人类的视觉系统理想地适应自然景色的处理,由亮度分量l,和两个色度分量α和β组成。其中,α表示黄一蓝通道(yellow—blue opponent),β表示红一绿通道(red—green opponent),见图3。
图3 lαβ色彩空间
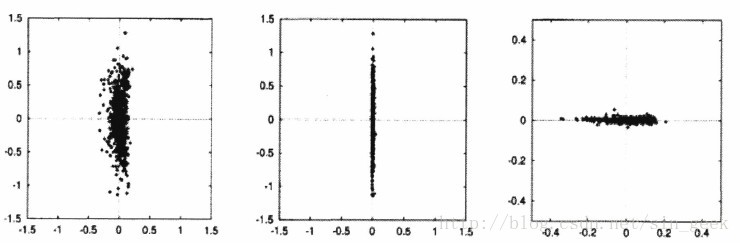
Ruderman等人在一幅用lαβ色彩空间表示的图像中随机抽取1000个像素点,生成了图4所示的坐标关系图。从中可以看出,lαβ色彩空间不仅基本消除了颜色分量之间的强相关性,而且有效地将图像的灰度信息和颜色信息分离开来。所以可以分别对三个通道图像进行独立的运算,而不需要修改另外两个通道的信息,从而不会影响原图像的自然效果。
图4 lab空间l-a、l-b、a-b关系图
色彩空间的转换
色彩空间一方面要符合人眼的视觉感知特性,另一方面应方便图像的处理。图像色彩迁移的过程是一个改变图像颜色基调的过程,通常希望在改变图像的一个颜色属性时,不改变图像其它的颜色属性。由前面的介绍可知,RGB空间的三通道具有很强的相关性,而lαβ空间的各通道具有最小的相关性。所以,在lαβ空间对图像的颜色进行出来将会变得十分方便。因此,选择在lαβ空间进行图像间的色彩迁移,这就需要将图像从RGB空间转换到lαβ空间。
1.从RGB空间到lαβ空间的转换
需要进行3次变换,即RGB->CIEXYZ->LMS->lαβ,具体步骤如下:
1)从RGB空间到CIE XYZ空间的转换
2)从CIE XYZ空间到LMS空间的转换
通过1、2可以得到RGB空间到LMS空间的转换
由于数据在LMS空间比较分散,所以进一步将其转换到以10为底的对数空间,这样不仅使数据分布更加聚敛,而且符号人类对于颜色感觉的心理物理学研究结果。
3)从LMS空间到lαβ空间的转换
这一变换是基于对数据的主成分分析(PCA,Principal ComponentAnalysis)得到的,其中l为第一主成分,α为第二主成分,β为第三主成分。
经过这三个步骤就完成了从RGB空间到lαβ空间的转换。
色彩空间的逆转换
当图像在lαβ空间进行处理之后,为了显示处理的结果,需要把图像转换到RGB空间,具体步骤为:
1)从lαβ空间到LMS对数空间的转换
2)从LMS对数空间到LMS线性空间的转换
3)从LMS空间到RGB空间的转换
添加上C/C++代码
- void RgbToLab(BYTE R,BYTE G,BYTE B,double& l,double& a,double& b)
- {
- double L = 0.3811*R + 0.5783*G + 0.0402*B;
- double M = 0.1967*R + 0.7244*G + 0.0782*B;
- double S = 0.0241*R + 0.1288*G + 0.8444*B;
- //若RGB值均为0,则LMS为0,防止数学错误log0
- if(L!=0) L = log(L)/log(10);
- if(M!=0) M = log(M)/log(10);
- if(S!=0) S = log(S)/log(10);
- l = (L + M + S)/sqrt(3);
- a = (L + M - 2*S)/sqrt(6);
- b = (L - M)/sqrt(2);
- }
- void LabToRgb(double l,double a,double b,BYTE& R,BYTE& G,BYTE& B)
- {
- l /= sqrt(3);
- a /= sqrt(6);
- b /= sqrt(2);
- double L = l + a + b;
- double M = l + a - b;
- double S = l - 2*a;
- L = pow(10,L);
- M = pow(10,M);
- S = pow(10,S);
- double dR = 4.4679*L - 3.5873*M + 0.1193*S;
- double dG = -1.2186*L + 2.3809*M - 0.1624*S;
- double dB = 0.0497*L - 0.2439*M + 1.2045*S;
- //防止溢出,若求得RGB值大于255则置为255,若小于0则置为0
- if (dR>255) R=255;
- else if (dR<0) R=0;
- else R = BYTE(dR);
- if (dG>255) G=255;
- else if (dG<0) G=0;
- else G = BYTE(dG);
- if (dB>255) B=255;
- else if (dB<0) B=0;
- else B = BYTE(dB);
- }








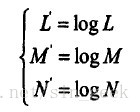
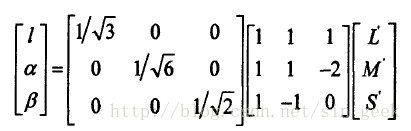
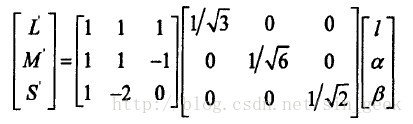
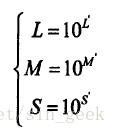

















 874
874

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








