打印输出1-n的所有全排序列

刷题的时候看到这样一个题：打印输出1-9的所有全排序列。后来想了一会，算是理会了，好记性不如烂笔头赶紧写一写加深一点理解。

看到这个问题，我们比较直观的想法就是每交换一次就做一次打印输出，但是要求控制好不能出现重复的序列。接下来以1-4的情况来作分析。

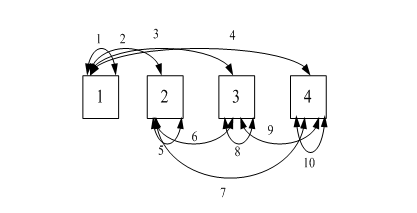
如上图，把第一位的交换（第1位与第1,2,3,4位的交换）分别编号为1,2,3,4. 类似的第2位的交换（第2位与第2,3,4位的交换）分别编号为5，6,7,。同理第3位的交换（第3位的与第3,4位的交换），第4位与自己的交换记为10 。

我们知道对于1-n个数的所有全排数为n!  我们可以这样考虑：

第1位我们做4次交换，对于第1位的每一种情况，后面3位再做全排，同样的第2位的每一种情况后两位也做一次全排，这样到了最后一位就打印输出。

当第一位取1时，我们知道这种全排种类数为 3！= 6 。当第一位和后面3位分别交换变成2,3,4后分别有6种情况，而后面除最后一位外的交换情况又是类似的，因此可以考虑利用递归的方法实现。

递归实现的步骤如下：

1）做第一位编号为1的交换（即1和自己交换），完了到下一位去做编号为5的交换࿰