1. 编辑距离定义
今天我们来研究一个有趣的算法题,叫做字符串编辑距离。编辑距离研究的问题和最长公共子序列有相似之处,都是比较两个字符串之间的相似性,只是采用的标准不太相同。
先给出编辑距离的定义:设A和B是2个字符串,要用最少的字符操作将字符串A转换为字符串B。这里所说的字符操作包括:
(1)删除一个字符(delete);
(2)插入一个字符(insert);
(3)将一个字符改为另一个字符(substitute)。
将字符串A变换为字符串B所用的最少字符操作数称为字符串A到B的编辑距离(edit distance)。通常情况下,三种操作的代价是一样的,也即每种字符操作都会导致一次变换,这也符合我们平常的认知。但是,有时也可以对这三种操作施加不同的影响因子,使算法倾向于某种变换,可以通过修改三种操作的代价来实现。
事实上,也可以包含更多的字符操作。例如,在英文输入的过程中经常会出现不小心交换两个字符的问题(trueàture),所以可以增加一个新的操作—置换(transposition),表示互换相邻的两个字符,此时编辑距离升级为Damerau–Levenshteindistance距离,它包含插入、删除、替换和置换四种操作。在OCR应用中还存在其他操作:将两个字符合并(merge)成一个或者将一个字符展开(split)成两个。当然,也可以减少字符操作,例如求两个等长字符串的汉明距离只用到了替换操作;还有,在求最长公共子序列(LCS)的问题中,其实等价于我们只采用插入和删除两种操作,虽然在LCS问题中求的是公共序列,我们也可以求它们之间的简化版编辑距离。
2. 编辑距离性质
编辑距离具有下面几个性质:
- 两个字符串的最小编辑距离至少是两个字符串的长度差;
- 两个字符串的最大编辑距离至多是两字符串中较长字符串的长度;
- 两个字符串的编辑距离是零的充要条件是两个字符串相同;
- 如果两个字符串等长,编辑距离的上限是汉明距离(Hamming distance);
- 编辑距离满足三角不等式,即d(a, c) ≤ d(a, b) + d(b, c);
- 如果两个字符串有相同的前缀或后缀,则去掉相同的前缀或后缀对编辑距离没有影响,其他位置不能随意删除。
3. 编辑距离的应用
编辑距离应用很广,最初的应用是拼写检查和近似字符串匹配。在生物医学领域,科学家将DNA看成有A,S,G,T构成的字符串,然后采用编辑距离判断不同DNA的相似度。关于近似字符串匹配,LCS也是一个不错的选择,在不同的问题中都有自己的用武之地。
编辑距离另一个很好的用途在语音识别中,它被当作一个评测指标。语音测试集的每一句话都有一个标准答案,然后利用编辑距离判断识别结果和标准答案之间的不同。不同的错误可以反映识别系统存在的问题。假如识别结果中插入错误较多,表示识别结果丢字很多,一个可能的原因是VAD做得不好;又或者识别结果中替换错误较多,则很有可能是训练过程中的语言模型不好。
再看一个应用,在linux下我们经常会用diff命令或者vimdiff命令按行比较两个文件的不同。运行命令之后会展示出两个文件的不同,展示方式其实就是按照编辑距离来定义的:哪个位置插入多少行或者删除多少行或者替换哪几行。所以我们可以用编辑距离来实现diff命令。
3. 算法实现
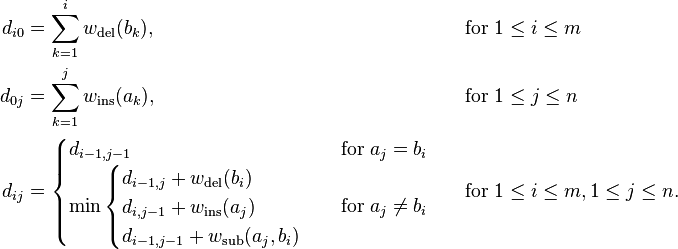
该问题和LCS一样,也是利用动态规划来解决。定义dij表示长度为i的字符串a变为长度为j的字符串b需要的编辑距离。需要注意的一点是,如果字符串a的最终长度为m,字符串b的最终长度为n,则d矩阵是一个(m+1)*(n+1)的矩阵,因为它可以表示长度为0的字符串之间的转换。它的递推式满足:
我们解释一下上面的公式,前两行是初始化,分别表示字符串b和a为空时对应的编辑距离计算。当字符串b为空时,我们将a变为b只需要不停地删除字符即可,反之则不停地添加字符。初始化完矩阵d的最初一行和一列之后我们就可以按照第三行公式去计算矩阵的剩余元素。第(i,j)个元素在计算的时候依赖于和它相邻的三个位置 (i-1,j-1)、(i,j-1)和(i-1,j)。公式的整体结构和LCS,DTW都非常像,唯一存在的难点就是到底哪一个位置对应删除操作,哪一个位置对应插入操作。 **由公式可以看出,(i-1,j)对应删除操作,(i,j-1)对应插入操作。可以这样理解,现在耗费了di-1,j步操作将字符串a(1,i-1)转换成了b(1,j),则在将a(1,i)转换成b(1,j)时,我们可以直接删掉字符a(i),问题变成a(1,i-1)转换成b(1,j),从而dij就等于di-1,j+1。同理,现在耗费了di,j-1步操作将字符串a(1,i)转换成了b(1,j-1),则在将a(1,i)转换成b(1,j)时,我们可以将b(j)添加到a(1,i)末尾(此时a(1,i)已转换成b(1,j-1))构成b(1,j)。**对应的代码实现如下:
/*
* 计算a->b的编辑距离
* dist[i][j]表示长度为i的字符串变为长度为j的字符串需要的编辑距离
* operation[i][j]表示变换过程中对应的操作
* 0:正确;1:字符替换;2:插入;3:删除
*/int edit_distance(char* a,char* b)
{
int len_a=strlen(a);
int len_b=strlen(b);
//b为空字符串,将a变为b需要不停地删除a的字符
for (int i=0;i<=len_a;i++)
{
dist[i][0]=i;
operation[i][0]=3;
}
//a为空字符串,将a变为b需要不停地添加b的字符
for (int j=0;j<=len_b;j++)
{
dist[0][j]=j;
operation[0][j]=2;
}
operation[0][0]=0;
for (int i=1;i<=len_a;i++)
{
for (int j=1;j<=len_b;j++)
{
int cost = (a[i-1] == b[j-1] ? 0 : 1);
int deletion = dist[i-1][j] + 1;
int insertion = dist[i][j-1] + 1;
int substitution = dist[i-1][j-1] + cost;
//如果不回溯直接利用下面这句
//dist[i][j] = MIN(deletion,MIN(insertion,substitution));
if(deletion>insertion)
{
if(substitution>insertion)
{
dist[i][j]=insertion;
operation[i][j]=2;
}
else
{
dist[i][j]=substitution;
operation[i][j]=cost;
}
}
else
{
if(substitution>deletion)
{
dist[i][j]=deletion;
operation[i][j]=3;
}
else
{
dist[i][j]=substitution;
operation[i][j]=cost;
}
}
}
}
return dist[len_a][len_b];
}
很多情况下,我们并不单纯地求编辑距离,还要把具体的操作步骤求出来,这可以通过回溯上面代码计算出的operation矩阵完成,回溯代码如下:
void backtrace(int operation[][MAX_LEN+1],char* a,char* b)
{
int insertion=0,deletion=0,substitution=0;
int i,j;
int len1=strlen(a);
int len2=strlen(b);
for (i=len1,j=len2;i>=0&&j>=0;)
{
switch(operation[i][j])
{
case 0:
//printf("(%d,%d) right\n",i,j);
printf("pos %d right\n",i);
i--;
j--;
continue;
case 1:
//printf("(%d,%d) substitute\n",i,j);
printf("pos %d substitute (%c-->%c)\n",i,a[i-1],b[j-1]);
i--;
j--;
substitution++;
continue;
case 2:
//printf("(%d,%d) insert\n",i,j);
printf("pos %d insert (%c)\n",i,b[j-1]);
j--;
insertion++;
continue;
case 3:
//printf("(%d,%d) delete\n",i,j);
printf("pos %d delete (%c)\n",i,a[i-1]);
i--;
deletion++;
continue;
}
}
printf("insert:%d,delete:%d,substitute:%d\n",insertion,deletion,substitution);
}
编辑距离作为一个经典的字符串动态规划题目,具有非常重要的应用,希望大家能熟练掌握。






















 1238
1238

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








