信息率失真函数

 

信息率失真函数

       在实际问题中，信号有一定得失真是可以容忍的。但是当失真大于某一个限度时，信息质量就会有严重损伤。要规定失真限度，必须有一个定量的失真测度。为此，可以引入失真函数。

       失真函数：

       假若一个数据处理系统，输入样值为x_i，x_i∈{a₁,...,a_n}，输出y_j，y_j∈{b₁,...,b_m}。此时定义失真函数：

 

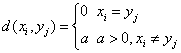
将所有的d(x_i,y_j)排列起来，用矩阵表示：

 

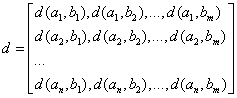
通常情况下，失真函数d(xi,yj)都是人为设定的。常用的失真函数如下：

均方失真：d(x_i,y_j)=(x_i-y_j)²

绝对失真：d(x_i,y_j)=| x_i-y_j|

相对失真：d(x_i,y_j)=| x_i-y_j|/|x_i|

误码失真：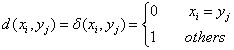

平均失真：

定义失真的数学期望为平均失真：

 

其中p(a_i,b_j)是联合分布概率。平均失真是对于信源编码器产生失真后的总体度量。对于长度为L的序列编码情况，平均失真为：

信息率失真函数R(D)：

信源X经过有失真的信源编码器输出Y，将这样的编码器看作存在干扰的假象信道，Y作为接收端信号。信源编码器的目的是使所需的信息传输率R尽量小，但R越小，引起的平均失真就越大。给出一个失真的限制值D，在满足平均失真的条件下，选择一种编码使时，信息率R尽可能小。信息率R就是所需输出的有关信源X的信息量。而信息率R其实就是互信息I(X,Y)。

可知，当信源的分布概率已知时，互信息I是关于转移概率p(y_j|x_i)的∪型凸函数，存在极小值。因此定义率失真函数R(D)：

 

对于离散无记忆信源，R(D)可以写成：

 

率失真函数的性质：

定义D_min=0对应着无失真情况，相当于无噪声信道，此时：

R(D_min)=R(0)=H(X)

定义 ，即R(D_max)=0。

可知R(D)的定义域为[0,D_max]。R(D)=0的情况就是I(X,Y)=0，这时候信道的输入和输出相互独立，所以条件概率p_ij与x_i无关，即：p_ij=p(y_j|x_i)=p(y_j)=p_j

此时平均失真为： 。

现在要记住： 。要求的 。在这个式子中，当某项∑p_id_ij最小，而该j所对应的p_j=1时，D_max达到最小。此时上式可以简化为： 。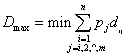

R(D)的重要性质：下凸性、连续性、单调递减性(就是JPEG2000那条著名的曲线)。