matlab——NN代码(nnsetup)解析

本片主要介绍一种对于网络参数的改进方式，这也是大牛Hinton在前两年对深度网络的一个工作，主要的方法就是dropout，思想就是在训练网络的时候随机扔掉一些网络权值进行训练，其方法在前面的

DeepLearnToolbox

工具箱中也有集成，通过在这个工具箱中设置dropout参数可以直接实现网络中加入dropout的算法思想，本文旨在研究该工具箱时涉及到了dropout这块然后希望弄明白这块。

关于dropout，工具箱中给出的参考文献为：http://www.cs.toronto.edu/~hinton/absps/dropout.pdf

源文章来源于:Improving neural networks by preventing co-adaptation of feature detectors

另外一个也是Hinton讲该方法的应用的： 
Dropout: A Simple Way to Prevent Neural Networks from Overtting

这个网络改进方法实质上就是为了防止网络参数的过拟合，尤其是小样本训练的时候是机器容易过拟合的。 
关于dropout，网上大神tornadomeet已经写的很详细了，并且附带一些这个工具箱下的实验，非常棒的，可以直接去看：(Dropout简单理解)

这里再简单分享一下我看的Dropout: A Simple Way to Prevent Neural Networks from Overtting 这篇文献下的一些笔记：

文章的摘要简单翻如下： 
深度神经网络是一个拥有众多参数的强大的机器学习系统。然而对于这种的网络来说过拟合是一个非常严重的问题。大型网络使用起来也很慢，从而在测试时面对如此大的网络是很难克服过拟合问题的。丢失数据技术(dropout)能够解决这个问题。这种方法的关键步骤在于训练时随机丢失网络的单元包括与之连接网络权值。在训练的时候，丢失网络单元的方法也可以是的网络变得更为稀薄紧凑。在测试阶段，也可以使用这种稀薄的网络更容易的预测网络的输出。这种方式有效的减少了网络的过拟合问题，并且比其他的规则化的方法有了明显的提升。同时我们也展示了这种丢失数据的方法用于监督学习实例上，比如视觉处理、语音识别、文本分类和计算机生物学上对应用，在大多数数据集上该方法都表现出目前最优的效果。

一个典型的dropout小结构就如下面这样子： 
 
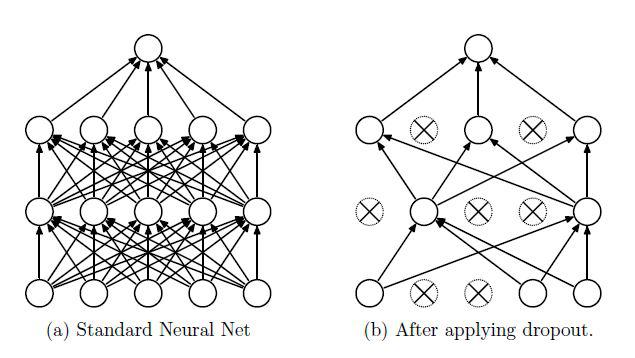
这就是一般正规的网络与随机dropout网络，其实那些没有连接上的单元也有连接，不过其上面的权值为0而已，这样表现出来就是相当于丢掉了一些单元了。至于丢掉的是那些单元呢？这个就是随机的了，丢掉的比例也是可以设置的。

其实说白了dropout就这么点东西，训练的时候随机丢掉一些权值，这样为什么可以防止过拟合呢？很自然，选择的单元少了，那么就没有那么苛刻的要求，自然训练起来的自由度大，也就是不太容易过拟合了。

上述文章后面是对DBN网络的dropout一些数学上的表述等等，然后是实验结果证明了这种方法的可靠性与防止过拟合性，并且确实能够带来性能一定程度的提升。

下面看看DeepLearnToolbox这个工具箱中关于dropout部分说明。 
这里先拿第五节

深度学习系列（五）：一个简单深度学习工具箱

中的nnsetup来说，这是网络的初始化函数，该工具箱的所有的网络都是需要先通过这个函数建立：

function nn = nnsetup(architecture)
%NNSETUP创建前向反馈神经网络
% nn = nnsetup(architecture) 返回一个神经网络结构，architecture为结构参数
% architecture 是一个n x 1 向量，表示每一层神经元的个数
%比如architecture=[784 100 10]，表示输入层为784维输入，100个隐含层，10个输出层
%为什么是输入为784：因为每一个手写体大小为28*28的，也就是784维度
%隐含层为什么是100：随便设置的，可以随意修改，需要设计
%输出为什么是10：手写体有0-9这10种结果，所以为10
 
    nn.size   = architecture;
    nn.n      = numel(nn.size);

    nn.activation_function              = 'tanh_opt';   % 隐含层激活函数: 'sigm' (sigmoid) or 'tanh_opt' (默认 tanh).
    nn.learningRate                     = 2;            %  学习率: typically needs to be lower when using 'sigm' activation function and non-normalized inputs.
    nn.momentum                         = 0.5;          %  Momentum 权值动量因子
    nn.scaling_learningRate             = 1;            %  学习率变化因子 (each epoch)
    nn.weightPenaltyL2                  = 0;            %  L2 regularization
    nn.nonSparsityPenalty               = 0;            %  非稀疏惩罚
    nn.sparsityTarget                   = 0.05;         %  稀疏目标值
    nn.inputZeroMaskedFraction          = 0;            %  自动编码的去噪作用
    nn.dropoutFraction                  = 0;            %  一种网络改进方式（dropout）Dropout level (http://www.cs.toronto.edu/~hinton/absps/dropout.pdf)
    nn.testing                          = 0;            %  一个标志参数--在nntest.m这个函数中会用到
    nn.output                           = 'sigm';       %  输出激活output unit 'sigm' (=logistic), 'softmax' and 'linear'

    for i = 2 : nn.n   
        % weights and weight momentum
        nn.W{i - 1} = (rand(nn.size(i), nn.size(i - 1)+1) - 0.5) * 2 * 4 * sqrt(6 / (nn.size(i) + nn.size(i - 1)));
        nn.vW{i - 1} = zeros(size(nn.W{i - 1}));

        % average activations (for use with sparsity)
        nn.p{i}     = zeros(1, nn.size(i));   
    end
end
 
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

在这里可以详细说明各个设置的详细含义了，注释上也可以看出。这里在一一说明一下：

（1） nn.activation_function 隐含层激活函数（不包括输出层，输出层的在nn.output ）。 
也就是下面这个东西，它有2个激活函数： ‘sigm’ (sigmoid) or ‘tanh_opt’ 

（2）nn.learningRate学习率，就是权值更新的时候增加或者减少的速率。这个在所有网络权值误差都计算好了以后会用到。像在这个工具箱下网络训练函数nntrain中有下面3行：

nn = nnff(nn, batch_x, batch_y);
nn = nnbp(nn);
nn = nnapplygrads(nn);
 
 
1
2
3

这三个函数可谓核心函数， 
第一个计算正向网络的每一层网络的输出； 
第二个函数利用反向传播算法计算各层的误差； 
第三个函数就是利用上述的误差来依次更新整个网络的权值；

那么这个nn.learningRate学习率很明显就会存在第三个函数中，打开如下：

function nn = nnapplygrads(nn)
%NNAPPLYGRADS updates weights and biases with calculated gradients
% nn = nnapplygrads(nn) returns an neural network structure with updated
% weights and biases
    for i = 1 : (nn.n - 1)
        %L2范数约束项
        if(nn.weightPenaltyL2>0)
            dW = nn.dW{i} + nn.weightPenaltyL2 * [zeros(size(nn.W{i},1),1) nn.W{i}(:,2:end)];
        else
            dW = nn.dW{i};
        end
        %误差学习速率
        dW = nn.learningRate * dW;
        %误差动量学习率
        if(nn.momentum>0)
            nn.vW{i} = nn.momentum*nn.vW{i} + dW;%因为初始化nn.vW{i}为0，所以nn.vW{i}最先的赋给的值就是 dw，然后在下次循环中，得出求导得到的dw乘上学习率就是应用的dw,在通过nn.vW{i} = nn.momentum*nn.vW{i} + dw，得到最终应用的dw            dW = nn.vW{i};
        end
        %更新
        nn.W{i} = nn.W{i} - dW;
    end
end
 
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

可以看到是有吧，同时还包括了L2范数约束项和动量学习率这两个参数，这也是nnsetup中有的。

（3）nn.momentum权值动量因子，这个东西的位置就是上面我们说到了的。这个加上到底什么意思呢，我们知道每一次误差反向传播的时候都会在每一层出现权值误差增量吧，新的权值是旧权值加上这个增量。但是我们还想考虑这一次的权值与上一次的权值误差增量之间的关系，不光是这一次权值误差增量，这样我们就设计了在不同代之间误差增量之间的一个量，这个量就是权值动量。直白的说就是这一次的权值更新还要考虑以前代的误差，不至于让权值跳的太快了，至于考虑以前的权值考虑多少就是这个因子了momentum。所以表现出来就是这样子

  %误差动量学习率
        if(nn.momentum>0)
            nn.vW{i} = nn.momentum*nn.vW{i} + dW;
            dW = nn.vW{i};
        end
 
 
1
2
3
4
5

可以看到nn.vW{i}就是上一次记录下的误差然后更新，最后在送给dw。

（4）nn.scaling_learningRate这个参数什么呢？对于不同的循环代数，学习率变化因子 (each epoch)。也就是不同的大循环次数，nn.learningRate的变化率。这个大循环是什么呢？就是opts.numepochs = 1;设置的参数，就是来回循环的次数，在nnstrain中也可以看到一个循环

for i = 1 : numepochs
 
 
1

在这个循环中然后执行一次大的训练，之后再拿训练好的网络以及原始的样本在进行numepochs次训练。在这个循环的末尾可以看到：

nn.learningRate = nn.learningRate * nn.scaling_learningRate;
 
 
1

就是nn.learningRate变化，默认nn.scaling_learningRate=1的话，也就是每一次大循环nn.learningRate是不变的。一般numepochs也就等于1，循环一次行了。当然肯定是越多网络训练的越好的。

那么再来谈谈这个值得用途，我们知道nn.learningRate太大，权值就跳的太快，不容易收敛，太小，收敛太慢，无法在指定的步内达到最优，所以nn.learningRate的设置是很重要的。那么一般的优化思想是什么样子的呢？首先给定一个较大的nn.learningRate让其广度搜索，逐步减小nn.learningRate的值，让其进行深度搜索，在这种思想下，一般就可以很好的收敛了，这种思想典型的就是用在模拟退火算法中，在那里降温的速率上就是如此，详细的可以翻我很前面的关于优化算法中模拟退火部分。

（5）nn.weightPenaltyL2 这一项就是L2范数约束项，其实也是为了限制权值的范围的。类似的还有L1范数约束，那么它在程序中的位置也是上面说的的那个nnapplygrads函数：

        %L2范数约束项
        if(nn.weightPenaltyL2>0)
            dW = nn.dW{i} + nn.weightPenaltyL2 * [zeros(size(nn.W{i},1),1) nn.W{i}(:,2:end)];
        else
            dW = nn.dW{i};
        end
 
 
1
2
3
4
5
6

这一项就是使得权值误差的大小与权值本身建立联系，至于为什么L2范数是这么表示的还不清楚，求高手解答。

（6）nn.nonSparsityPenalty非稀疏惩罚，目的就是使得每一层的权值之和尽可能小，这样就强迫每一个权值不能太大，从而使得大多数权值较小以至于为0，这就是稀疏性。这在前面稀疏性表达的时候详细介绍过，可以去看看。

（7）nn.sparsityTarget 稀疏目标值，这和nn.nonSparsityPenalty联合在一起使用。其目标值就是每一层的网络权值之和的这个值。比如说为0.05，那么这一层的网络权值在优化的时候，其权值之和就会往0.05上面靠近。 
在程序中就是在nnbp函数里面，在那里可以找到：

  if(nn.nonSparsityPenalty>0)
            pi = repmat(nn.p{i}, size(nn.a{i}, 1), 1);
            sparsityError = [zeros(size(nn.a{i},1),1) nn.nonSparsityPenalty * (-nn.sparsityTarget ./ pi + (1 - nn.sparsityTarget) ./ (1 - pi))];
        end
 
 
1
2
3
4

（8）nn.inputZeroMaskedFraction在输入中加入噪声的作用，其本质上也是增加网络的抗噪能力与过拟合效应。这个是怎么加的呢？其实就是使得原始输入的一个样本中中某一些数据随机置为0。我们说dropout是在网络上使得网络的权值随机置为0，而这里是把数据输入随机一部分置为0，这简直是一个对外抗干扰，一个对内抗干扰，目的都是在于增加系统的鲁棒性。 
这一项在nntrain中可以看到：

 %Add noise to input (for use in denoising autoencoder)
        if(nn.inputZeroMaskedFraction ~= 0)
            batch_x = batch_x.*(rand(size(batch_x))>nn.inputZeroMaskedFraction);
        end
 
 
1
2
3
4

（9）再就是本文开头说的改进方式,nn.dropoutFraction ,一种网络改进方式（dropout）。详细的说明在开始已经说了就不再说了。

回头看看，其实可以发现，这个工具箱其实把大多数该考虑的、目前有的优化思想都集成到里面去了，确是不错的。 
好了，至于更详细的可以看论文，以及去看这个工具箱的代码来理解吧。