batch normalization

20210702

深度学习中的五种归一化（BN、LN、IN、GN和SN）方法简介
https://blog.csdn.net/u013289254/article/details/99690730

https://cloud.tencent.com/developer/article/1500846
常用的 Normalization 方法：BN、LN、IN、GN

常用的 Normalization 方法：BN、LN、IN、GN（附代码＆链接）
https://mp.weixin.qq.com/s/j4LS4rDE5nfRy3CcWAre4A

https://blog.csdn.net/kyle1314608/article/details/118422495
白化

https://mp.weixin.qq.com/s/eeIF9zWf-dWmvXvbXmfhCg
深入理解Batch Normalization

20210614

https://www.cnblogs.com/wlk12580/p/13651673.html

pytorch torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)

此函数的作用是对输入的每个batch数据做归一化处理,目的是数据合理分布，加速计算过程，函数为：

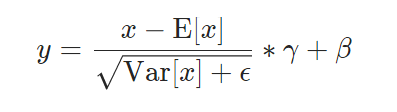
num_features:为输入的数据的通道数,
eps：使分母不为零，保持数据的稳定
momentum:用于在训练时对均值和方差的估计
affine：为True时表示γ和β是可学习的参数，为False表示γ和β是不可学习的参数，此时γ=1，β=0；
track_running_stats=True;整个batch的方差和均值

https://blog.csdn.net/qq_39777550/article/details/108038677
重点

一、背景意义

本篇博文主要讲解2015年深度学习领域，非常值得学习的一篇文献：《Batch Normalization: Accelerating Deep Network Training by  Reducing Internal Covariate Shift》，这个算法目前已经被大量的应用，最新的文献算法很多都会引用这个算法，进行网络训练，可见其强大之处非同一般啊。

近年来深度学习捷报连连、声名鹊起，随机梯度下架成了训练深度网络的主流方法。尽管随机梯度下降法对于训练深度网络简单高效，但是它有个毛病，就是需要我们人为的去选择参数，比如学习率、参数初始化、权重衰减系数、Drop out比例等。这些参数的选择对训练结果至关重要，以至于我们很多时间都浪费在这些的调参上。那么学完这篇文献之后，你可以不需要那么刻意的慢慢调整参数。BN算法（Batch Normalization）其强大之处如下：

(1)你可以选择比较大的初始学习率，让你的训练速度飙涨。以前还需要慢慢调整学习率，甚至在网络训练到一半的时候，还需要想着学习率进一步调小的比例选择多少比较合适，现在我们可以采用初始很大的学习率，然后学习率的衰减速度也很大，因为这个算法收敛很快。当然这个算法即使你选择了较小的学习率，也比以前的收敛速度快，因为它具有快速训练收敛的特性；

(2)你再也不用去理会过拟合中drop out、L2正则项参数的选择问题，采用BN算法后，你可以移除这两项了参数，或者可以选择更小的L2正则约束参数了，因为BN具有提高网络泛化能力的特性；

(3)再也不需要使用使用局部响应归一化层了（局部响应归一化是Alexnet网络用到的方法，搞视觉的估计比较熟悉），因为BN本身就是一个归一化网络层；

(4)可以把训练数据彻底打乱（防止每批训练的时候，某一个样本都经常被挑选到，文献说这个可以提高1%的精度，这句话我也是百思不得其解啊）。

原理

开始讲解算法前，先来思考一个问题：我们知道在神经网络训练开始前，都要对输入数据做一个归一化处理，那么具体为什么需要归一化呢？归一化后有什么好处呢？原因在于神经网络学习过程本质（重点）就是为了学习数据分布，一旦训练数据与测试数据的分布不同，那么网络的泛化能力也大大降低；另外一方面，一旦每批训练数据的分布各不相同(batch 梯度下降)，那么网络就要在每次迭代都去学习适应不同的分布，这样将会大大降低网络的训练速度，这也正是为什么我们需要对数据都要做一个归一化预处理的原因。

对于深度网络的训练是一个复杂的过程，只要网络的前面几层发生微小的改变，那么后面几层就会被累积放大下去。一旦网络某一层的输入数据的分布发生改变，那么这一层网络就需要去适应学习这个新的数据分布，所以如果训练过程中，训练数据的分布一直在发生变化，那么将会影响网络的训练速度。

我们知道网络一旦train起来，那么参数就要发生更新，除了输入层的数据外(因为输入层数据，我们已经人为的为每个样本归一化)，后面网络每一层的输入数据分布是一直在发生变化的，因为在训练的时候，前面层训练参数的更新将导致后面层输入数据分布的变化。以网络第二层为例：网络的第二层输入，是由第一层的参数和input计算得到的，而第一层的参数在整个训练过程中一直在变化，因此必然会引起后面每一层输入数据分布的改变。我们把网络中间层在训练过程中，数据分布的改变称之为：“Internal  Covariate Shift”。Paper所提出的算法，就是要解决在训练过程中，中间层数据分布发生改变的情况，于是就有了Batch  Normalization，这个牛逼算法的诞生。

二、初识BN(Batch  Normalization)

1、BN概述

就像激活函数层、卷积层、全连接层、池化层一样，BN(Batch Normalization)也属于网络的一层。在前面我们提到网络除了输出层外，其它层因为低层网络在训练的时候更新了参数，而引起后面层输入数据分布的变化。这个时候我们可能就会想，如果在每一层输入的时候，再加个预处理操作那该有多好啊，比如网络第三层输入数据X3(X3表示网络第三层的输入数据)把它归一化至：均值0、方差为1，然后再输入第三层计算，这样我们就可以解决前面所提到的“Internal Covariate Shift”的问题了。

而事实上，paper的算法本质原理就是这样：在网络的每一层输入的时候，又插入了一个归一化层，也就是先做一个归一化处理，然后再进入网络的下一层。不过文献归一化层，可不像我们想象的那么简单，它是一个可学习、有参数的网络层。既然说到数据预处理，下面就先来复习一下最强的预处理方法：白化。

2、预处理操作选择

说到神经网络输入数据预处理，最好的算法莫过于白化预处理。然而白化计算量太大了，很不划算，还有就是白化不是处处可微的，所以在深度学习中，其实很少用到白化。经过白化预处理后，数据满足条件：a、特征之间的相关性降低，这个就相当于pca；b、数据均值、标准差归一化，也就是使得每一维特征均值为0，标准差为1。如果数据特征维数比较大，要进行PCA，也就是实现白化的第1个要求，是需要计算特征向量，计算量非常大，于是为了简化计算，作者忽略了第1个要求，仅仅使用了下面的公式进行预处理，也就是近似白化预处理：

公式简单粗糙，但是依旧很牛逼。因此后面我们也将用这个公式，对某一个层网络的输入数据做一个归一化处理。需要注意的是，我们训练过程中采用batch 随机梯度下降，上面的E(xk)指的是每一批训练数据神经元xk的平均值；然后分母就是每一批数据神经元xk激活度的一个标准差了。

三、BN算法实现

1、BN算法概述

经过前面简单介绍，这个时候可能我们会想当然的以为：好像很简单的样子，不就是在网络中间层数据做一个归一化处理嘛，这么简单的想法，为什么之前没人用呢？然而其实实现起来并不是那么简单的。其实如果是仅仅使用上面的归一化公式，对网络某一层A的输出数据做归一化，然后送入网络下一层B，这样是会影响到本层网络A所学习到的特征的。打个比方，比如我网络中间某一层学习到特征数据本身就分布在S型激活函数的两侧，你强制把它给我归一化处理、标准差也限制在了1，把数据变换成分布于s函数的中间部分，这样就相当于我这一层网络所学习到的特征分布被你搞坏了，这可怎么办？于是文献使出了一招惊天地泣鬼神的招式：变换重构，引入了可学习参数γ、β，这就是算法关键之处：

 

每一个神经元xk都会有一对这样的参数γ、β。这样其实当：

、

是可以恢复出原始的某一层所学到的特征的。因此我们引入了这个可学习重构参数γ、β，让我们的网络可以学习恢复出原始网络所要学习的特征分布。（重点）最后Batch Normalization网络层的前向传导过程公式就是：

 

上面的公式中m指的是mini-batch size。

2、源码实现

            m = K.mean(X, axis=-1, keepdims=True)#计算均值
            std = K.std(X, axis=-1, keepdims=True)#计算标准差
            X_normed = (X - m) / (std + self.epsilon)#归一化
            out = self.gamma * X_normed + self.beta#重构变换

3、实战使用

(1)可能学完了上面的算法，你只是知道它的一个训练过程，一个网络一旦训练完了，就没有了min-batch这个概念了。测试阶段我们一般只输入一个测试样本，看看结果而已。因此测试样本，前向传导的时候，上面的均值u、标准差σ 要哪里来？其实网络一旦训练完毕，参数都是固定的，这个时候即使是每批训练样本进入网络，那么BN层计算的均值u、和标准差都是固定不变的。我们可以采用这些数值来作为测试样本所需要的均值、标准差，于是最后测试阶段的u和σ 计算公式如下：

上面简单理解就是：对于均值来说直接计算所有batch u值的平均值；然后对于标准偏差采用每个batch σB的无偏估计。最后测试阶段，BN的使用公式就是：

(2)根据文献说，BN可以应用于一个神经网络的任何神经元上。文献主要是把BN变换，置于网络激活函数层的前面。在没有采用BN的时候，激活函数层是这样的：

z=g(Wu+b)

也就是我们希望一个激活函数，比如s型函数s(x)的自变量x是经过BN处理后的结果。因此前向传导的计算公式就应该是：

z=g(BN(Wu+b))

其实因为偏置参数b经过BN层后其实是没有用的，最后也会被均值归一化，当然BN层后面还有个β参数作为偏置项，所以b这个参数就可以不用了。因此最后把BN层+激活函数层就变成了：

z=g(BN(Wu))

四、Batch Normalization在CNN中的使用

通过上面的学习，我们知道BN层是对于每个神经元做归一化处理，甚至只需要对某一个神经元进行归一化，而不是对一整层网络的神经元进行归一化。既然BN是对单个神经元的运算，那么在CNN中卷积层上要怎么搞？假如某一层卷积层有6个特征图，每个特征图的大小是100*100，这样就相当于这一层网络有6*100*100个神经元，如果采用BN，就会有6*100*100个参数γ、β，这样岂不是太恐怖了。因此卷积层上的BN使用，其实也是使用了类似权值共享的策略，把一整张特征图当做一个神经元进行处理。

卷积神经网络经过卷积后得到的是一系列的特征图，如果min-batch sizes为m，那么网络某一层输入数据可以表示为四维矩阵(m,f,p,q)，m为min-batch sizes，f为特征图个数，p、q分别为特征图的宽高。在cnn中我们可以把每个特征图看成是一个特征处理（一个神经元），因此在使用Batch Normalization，mini-batch size 的大小就是：m*p*q，于是对于每个特征图都只有一对可学习参数：γ、β。说白了吧，这就是相当于求取所有样本所对应的一个特征图的所有神经元的平均值、方差，然后对这个特征图神经元做归一化。下面是来自于keras卷积层的BN实现一小段主要源码：

           input_shape = self.input_shape
            reduction_axes = list(range(len(input_shape)))
            del reduction_axes[self.axis]
            broadcast_shape = [1] * len(input_shape)
            broadcast_shape[self.axis] = input_shape[self.axis]
            if train:
                m = K.mean(X, axis=reduction_axes)
                brodcast_m = K.reshape(m, broadcast_shape)
                std = K.mean(K.square(X - brodcast_m) + self.epsilon, axis=reduction_axes)
                std = K.sqrt(std)
                brodcast_std = K.reshape(std, broadcast_shape)
                mean_update = self.momentum * self.running_mean + (1-self.momentum) * m
                std_update = self.momentum * self.running_std + (1-self.momentum) * std
                self.updates = [(self.running_mean, mean_update),
                                (self.running_std, std_update)]
                X_normed = (X - brodcast_m) / (brodcast_std + self.epsilon)
            else:
                brodcast_m = K.reshape(self.running_mean, broadcast_shape)
                brodcast_std = K.reshape(self.running_std, broadcast_shape)
                X_normed = ((X - brodcast_m) /
                            (brodcast_std + self.epsilon))
            out = K.reshape(self.gamma, broadcast_shape) * X_normed + K.reshape(self.beta, broadcast_shape)

个人总结：2015年个人最喜欢深度学习的一篇paper就是Batch Normalization这篇文献，采用这个方法网络的训练速度快到惊人啊，感觉训练速度是以前的十倍以上，再也不用担心自己这破电脑每次运行一下，训练一下都要跑个两三天的时间。另外这篇文献跟空间变换网络《Spatial Transformer Networks》的思想神似啊，都是一个变换网络层。

参考文献：

1、《Batch Normalization: Accelerating Deep Network Training by  Reducing Internal Covariate Shift》

2、《Spatial Transformer Networks》

3、https://github.com/fchollet/keras

20201203 1.nn.BatchNorm1d(num_features)

        1.对小批量(mini-batch)的2d或3d输入进行批标准化(Batch Normalization)操作
        2.num_features：
                来自期望输入的特征数，该期望输入的大小为'batch_size x num_features [x width]'
                意思即输入大小的形状可以是'batch_size x num_features' 和 'batch_size x num_features x width' 都可以。
                （输入输出相同）
                输入Shape：（N, C）或者(N, C, L)
                输出Shape：（N, C）或者（N，C，L）

          eps：为保证数值稳定性（分母不能趋近或取0）,给分母加上的值。默认为1e-5。
          momentum：动态均值和动态方差所使用的动量。默认为0.1。
          affine：一个布尔值，当设为true，给该层添加可学习的仿射变换参数。
        3.在每一个小批量（mini-batch）数据中，计算输入各个维度的均值和标准差。gamma与beta是可学习的大小为C的参数向量（C为输入大小）
          在训练时，该层计算每次输入的均值与方差，并进行移动平均。移动平均默认的动量值为0.1。
          在验证时，训练求得的均值/方差将用于标准化验证数据。 
        4.例子
                >>> # With Learnable Parameters
                >>> m = nn.BatchNorm1d(100) #num_features指的是randn(20, 100)中（N, C）的第二维C
                >>> # Without Learnable Parameters
                >>> m = nn.BatchNorm1d(100, affine=False)
                >>> input = autograd.Variable(torch.randn(20, 100)) #输入Shape：（N, C）
                >>> output = m(input)  #输出Shape：（N, C）

2.nn.BatchNorm2d(num_features)

        1.对小批量(mini-batch)3d数据组成的4d输入进行批标准化(Batch Normalization)操作
        2.num_features： 
                来自期望输入的特征数，该期望输入的大小为'batch_size x num_features x height x width'
                （输入输出相同）
                    输入Shape：（N, C，H, W)
                    输出Shape：（N, C, H, W）
          eps： 为保证数值稳定性（分母不能趋近或取0）,给分母加上的值。默认为1e-5。
          momentum： 动态均值和动态方差所使用的动量。默认为0.1。
          affine： 一个布尔值，当设为true，给该层添加可学习的仿射变换参数。
        3.在每一个小批量（mini-batch）数据中，计算输入各个维度的均值和标准差。gamma与beta是可学习的大小为C的参数向量（C为输入大小）
          在训练时，该层计算每次输入的均值与方差，并进行移动平均。移动平均默认的动量值为0.1。
          在验证时，训练求得的均值/方差将用于标准化验证数据。
        4.例子
            >>> # With Learnable Parameters
            >>> m = nn.BatchNorm2d(100) #num_features指的是randn(20, 100, 35, 45)中（N, C，H, W)的第二维C
            >>> # Without Learnable Parameters
            >>> m = nn.BatchNorm2d(100, affine=False)
            >>> input = autograd.Variable(torch.randn(20, 100, 35, 45))  #输入Shape：（N, C，H, W)
            >>> output = m(input)

3.nn.BatchNorm3d(num_features)

        1.对小批量(mini-batch)4d数据组成的5d输入进行批标准化(Batch Normalization)操作
        2.num_features： 
                来自期望输入的特征数，该期望输入的大小为'batch_size x num_features depth x height x width'
                （输入输出相同）
                 输入Shape：（N, C，D, H, W)
                 输出Shape：（N, C, D, H, W）

          eps： 为保证数值稳定性（分母不能趋近或取0）,给分母加上的值。默认为1e-5。
          momentum： 动态均值和动态方差所使用的动量。默认为0.1。
          affine： 一个布尔值，当设为true，给该层添加可学习的仿射变换参数。

        3.在每一个小批量（mini-batch）数据中，计算输入各个维度的均值和标准差。gamma与beta是可学习的大小为C的参数向量（C为输入大小）
          在训练时，该层计算每次输入的均值与方差，并进行移动平均。移动平均默认的动量值为0.1。
          在验证时，训练求得的均值/方差将用于标准化验证数据。
        4.例子
            >>> # With Learnable Parameters
            >>> m = nn.BatchNorm3d(100)  #num_features指的是randn(20, 100, 35, 45, 10)中（N, C, D, H, W）的第二维C
            >>> # Without Learnable Parameters
            >>> m = nn.BatchNorm3d(100, affine=False)  #num_features指的是randn(20, 100, 35, 45, 10)中（N, C, D, H, W）的第二维C
            >>> input = autograd.Variable(torch.randn(20, 100, 35, 45, 10)) #输入Shape：（N, C, D, H, W） 
            >>> output = m(input)

20201203
对特征维进行归一化

[batchsize feature] 用 BatchNorm1d
[batchsize feature H W] 用batchNorm2d
[batchsize feature X H W] x是什么 用 batchnorm3d

20201229
几种batch normalization的使用
笔者近来在tensorflow中使用batch_norm时，由于事先不熟悉其内部的原理，因此将其错误使用，从而出现了结果与预想不一致的结果。事后对其进行了一定的调查与研究，在此进行一些总结。

一、错误使用及结果
笔者最先使用时只是了解到了在tensorflow中tf.layers.batch_normalization这个函数，就在函数中直接将其使用，该函数中有一个参数为training，在训练阶段赋值True，在测试阶段赋值False。但是在训练完成后，出现了奇怪的现象时，在training赋值为True时，测试的正确率正常，但是training赋值为False时，测试正确率就很低。上述错误使用过程可以精简为下列代码段

is_traing = tf.placeholder(dtype=tf.bool)
input = tf.ones([1, 2, 2, 3])
output = tf.layers.batch_normalization(input, training=is_traing)
loss = ...
train_op = optimizer.minimize(loss)

with tf.Session() as sess:
	sess.run(tf.global_variables_initializer())
	sess.run(train_op)

二、batch_normalization
下面首先粗略的介绍一下batch_normalization，这种归一化方法的示意图和算法如下图，

总的来说就是对于同一batch的input，假设输入大小为[batch_num, height, width, channel]，逐channel地计算同一batch中所有数据的mean和variance，再对input使用mean和variance进行归一化，最后的输出再进行线性平移，得到batch_norm的最终结果。伪代码如下：

for i in range(channel):
	x = input[:,:,:,i]
	mean = mean(x)
	variance = variance(x)
	x = (x - mean) / sqrt(variance)
	x = scale * x + offset
	input[:,:,:,i] = x

在实现的时候，会在训练阶段记录下训练数据中平均mean和variance，记为moving_mean和moving_variance，并在测试阶段使用训练时的moving_mean和moving_variance进行计算，这也就是参数training的作用。另外，在实现时一般使用一个decay系数来逐步更新moving_mean和moving_variance，moving_mean = moving_mean * decay + new_batch_mean * (1 - decay)

三、tensorflow中的三种实现
tensorflow中关于batch_norm现在有三种实现方式。
1、tf.nn.batch_normalization（最底层的实现）

tf.nn.batch_normalization(
    x,
    mean,
    variance,
    offset,
    scale,
    variance_epsilon,
    name=None
)

该函数是一种最底层的实现方法，在使用时mean、variance、scale、offset等参数需要自己传递并更新，因此实际使用时还需自己对该函数进行封装，一般不建议使用，但是对了解batch_norm的原理很有帮助。
封装使用的实例如下：

import tensorflow as tf

def batch_norm(x, name_scope, training, epsilon=1e-3, decay=0.99):
    """ Assume nd [batch, N1, N2, ..., Nm, Channel] tensor"""
    with tf.variable_scope(name_scope):
        size = x.get_shape().as_list()[-1]
        scale = tf.get_variable('scale', [size], initializer=tf.constant_initializer(0.1))
        offset = tf.get_variable('offset', [size])

        pop_mean = tf.get_variable('pop_mean', [size], initializer=tf.zeros_initializer(), trainable=False)
        pop_var = tf.get_variable('pop_var', [size], initializer=tf.ones_initializer(), trainable=False)
        batch_mean, batch_var = tf.nn.moments(x, list(range(len(x.get_shape())-1)))
        train_mean_op = tf.assign(pop_mean, pop_mean * decay + batch_mean * (1 - decay))
        train_var_op = tf.assign(pop_var, pop_var * decay + batch_var * (1 - decay))

        def batch_statistics():
            with tf.control_dependencies([train_mean_op, train_var_op]):
                return tf.nn.batch_normalization(x, batch_mean, batch_var, offset, scale, epsilon)
        def population_statistics():
            return tf.nn.batch_normalization(x, pop_mean, pop_var, offset, scale, epsilon)

        return tf.cond(training, batch_statistics, population_statistics)

is_traing = tf.placeholder(dtype=tf.bool)
input = tf.ones([1, 2, 2, 3])
output = batch_norm(input, name_scope='batch_norm_nn', training=is_traing)

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    saver = tf.train.Saver()
    saver.save(sess, "batch_norm_nn/Model")

在batch_norm中，首先先计算了x的逐通道的mean和var，然后将pop_mean和pop_var进行更新，并根据是在训练阶段还是测试阶段选择将当批次计算的mean和var或者训练阶段保存的mean和var与新定义的变量scale和offset一起传递给tf.nn.batch_normalization

2、tf.layers.batch_normalization

tf.layers.batch_normalization(
    inputs,
    axis=-1,
    momentum=0.99,
    epsilon=0.001,
    center=True,
    scale=True,
    beta_initializer=tf.zeros_initializer(),
    gamma_initializer=tf.ones_initializer(),
    moving_mean_initializer=tf.zeros_initializer(),
    moving_variance_initializer=tf.ones_initializer(),
    beta_regularizer=None,
    gamma_regularizer=None,
    beta_constraint=None,
    gamma_constraint=None,
    training=False,
    trainable=True,
    name=None,
    reuse=None,
    renorm=False,
    renorm_clipping=None,
    renorm_momentum=0.99,
    fused=None,
    virtual_batch_size=None,
    adjustment=None
)

该函数也就是笔者之前使用的函数，在官方文档中写道

Note: when training, the moving_mean and moving_variance need to be updated. By default the update ops are placed in tf.GraphKeys.UPDATE_OPS, so they need to be added as a dependency to the train_op. Also, be sure to add any batch_normalization ops before getting the update_ops collection. Otherwise, update_ops will be empty, and training/inference will not work properly. For example:

  x_norm = tf.layers.batch_normalization(x, training=training)

  # ...

  update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS)
  with tf.control_dependencies(update_ops):
    train_op = optimizer.minimize(loss)

可以看到，与笔者之前的错误实现方法的差异主要在

update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS)
  with tf.control_dependencies(update_ops):

这两句话，同时可以看到在第一种方法tf.nn.batch_normalization的封装过程中也用到了类似的处理方法，具体会在下一段进行说明。

3、tf.contrib.layers.batch_norm(slim)

tf.contrib.layers.batch_norm(
    inputs,
    decay=0.999,
    center=True,
    scale=False,
    epsilon=0.001,
    activation_fn=None,
    param_initializers=None,
    param_regularizers=None,
    updates_collections=tf.GraphKeys.UPDATE_OPS,
    is_training=True,
    reuse=None,
    variables_collections=None,
    outputs_collections=None,
    trainable=True,
    batch_weights=None,
    fused=None,
    data_format=DATA_FORMAT_NHWC,
    zero_debias_moving_mean=False,
    scope=None,
    renorm=False,
    renorm_clipping=None,
    renorm_decay=0.99,
    adjustment=None
)

这种方法与tf.layers.batch_normalization的使用方法差不多，两者最主要的差别在参数scale和centre的默认值上，这两个参数即是我们之前介绍原理时所说明的对input进行mean和variance的归一化之后采用的线性平移中的scale和offset，可以看到offset的默认值两者都是True，但是scale的默认值前者为True后者为False，也就是说明在tf.contrib.layers.batch_norm中，默认不对处理后的input进行线性缩放，只是加一个偏移。

四、关于tf.GraphKeys.UPDATA_OPS
介绍到这里，还有两个概念没有介绍，一个是tf.GraphKeys.UPDATE_OPS，另一个是tf.control_dependencies。

1、tf.control_dependencies
首先我们先介绍tf.control_dependencies，该函数保证其辖域中的操作必须要在该函数所传递的参数中的操作完成后再进行。请看下面一个例子。

import tensorflow as tf
a_1 = tf.Variable(1)
b_1 = tf.Variable(2)
update_op = tf.assign(a_1, 10)
add = tf.add(a_1, b_1)

a_2 = tf.Variable(1)
b_2 = tf.Variable(2)
update_op = tf.assign(a_2, 10)
with tf.control_dependencies([update_op]):
    add_with_dependencies = tf.add(a_2, b_2)

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    ans_1, ans_2 = sess.run([add, add_with_dependencies])
    print("Add: ", ans_1)
    print("Add_with_dependency: ", ans_2)

输出：
Add:  3
Add_with_dependency:  12

可以看到两组加法进行的对比，正常的计算图在计算add时是不会经过update_op操作的，因此在加法时a的值为1，但是采用tf.control_dependencies函数，可以控制在进行add前先完成update_op的操作，因此在加法时a的值为10，因此最后两种加法的结果不同。

2、tf.GraphKeys.UPDATE_OPS
关于tf.GraphKeys.UPDATE_OPS，这是一个tensorflow的计算图中内置的一个集合，其中会保存一些需要在训练操作之前完成的操作，并配合tf.control_dependencies函数使用。
关于在batch_norm中，即为更新mean和variance的操作。通过下面一个例子可以看到tf.layers.batch_normalization中是如何实现的。

import tensorflow as tf

is_traing = tf.placeholder(dtype=tf.bool)
input = tf.ones([1, 2, 2, 3])
output = tf.layers.batch_normalization(input, training=is_traing)

update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS)
print(update_ops)
# with tf.control_dependencies(update_ops):
    # train_op = optimizer.minimize(loss)

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    saver = tf.train.Saver()
    saver.save(sess, "batch_norm_layer/Model")
    
 输出：
 [<tf.Tensor 'batch_normalization/AssignMovingAvg:0' shape=(3,) dtype=float32_ref>, <tf.Tensor 'batch_normalization/AssignMovingAvg_1:0' shape=(3,) dtype=float32_ref>]

可以看到输出的即为两个batch_normalization中更新mean和variance的操作，需要保证它们在train_op前完成。
这两个操作是在tensorflow的内部实现中自动被加入tf.GraphKeys.UPDATE_OPS这个集合的，在tf.contrib.layers.batch_norm的参数中可以看到有一项updates_collections的默认值即为tf.GraphKeys.UPDATE_OPS，而在tf.layers.batch_normalization中则是直接将两个更新操作放入了上述集合。

五、关于最初的错误使用的思考
最后我对于一开始的使用方法为什么会导致错误进行了思考，tensorflow中具体实现batch_normalization的代码在tensorflow\python\layers\normalization.py中，下面展示一些关键代码。

if self.scale:
    self.gamma = self.add_variable(
          name='gamma',
          shape=param_shape,
          dtype=param_dtype,
          initializer=self.gamma_initializer,
          regularizer=self.gamma_regularizer,
          constraint=self.gamma_constraint,
          trainable=True)
else:
    self.gamma = None
      
if self.center:
    self.beta = self.add_variable(
          name='beta',
          shape=param_shape,
          dtype=param_dtype,
          initializer=self.beta_initializer,
          regularizer=self.beta_regularizer,
          constraint=self.beta_constraint,
          trainable=True)
else:
    self.beta = None
    
scale, offset = _broadcast(self.gamma), _broadcast(self.beta)

self.moving_mean = self._add_tower_local_variable(
          name='moving_mean',
          shape=param_shape,
          dtype=param_dtype,
          initializer=self.moving_mean_initializer,
          trainable=False)

self.moving_variance = self._add_tower_local_variable(
          name='moving_variance',
          shape=param_shape,
          dtype=param_dtype,
          initializer=self.moving_variance_initializer,
          trainable=False)

def _assign_moving_average(self, variable, value, momentum):
    with ops.name_scope(None, 'AssignMovingAvg', [variable, value, momentum]) as scope:
        decay = ops.convert_to_tensor(1.0 - momentum, name='decay')
        if decay.dtype != variable.dtype.base_dtype:
            decay = math_ops.cast(decay, variable.dtype.base_dtype)
        update_delta = (variable - value) * decay
        return state_ops.assign_sub(variable, update_delta, name=scope)
 
def _do_update(var, value):
    return self._assign_moving_average(var, value, self.momentum)



# Determine a boolean value for `training`: could be True, False, or None.
training_value = utils.constant_value(training)
if training_value is not False:
    mean, variance = nn.moments(inputs, reduction_axes, keep_dims=keep_dims)
    moving_mean = self.moving_mean
    moving_variance = self.moving_variance
    mean = utils.smart_cond(training,
                              lambda: mean,
                              lambda: moving_mean)
    variance = utils.smart_cond(training,
                                  lambda: variance,
                                  lambda: moving_variance)
else:
    new_mean, new_variance = mean, variance
    
mean_update = utils.smart_cond(
          training,
          lambda: _do_update(self.moving_mean, new_mean),
          lambda: self.moving_mean)
variance_update = utils.smart_cond(
          training,
          lambda: _do_update(self.moving_variance, new_variance),
          lambda: self.moving_variance)
if not context.executing_eagerly():
    self.add_update(mean_update, inputs=inputs)
    self.add_update(variance_update, inputs=inputs)
outputs = nn.batch_normalization(inputs,
                                     _broadcast(mean),
                                     _broadcast(variance),
                                     offset,
                                     scale,
                                     self.epsilon)

可以看到其内部逻辑和我在介绍tf.nn.batch_normalization一节中展示的封装时所使用的方法类似。
如果不在使用时添加tf.control_dependencies函数，即在训练时(training=True)每批次时只会计算当批次的mean和var，并传递给tf.nn.batch_normalization进行归一化，由于mean_update和variance_update在计算图中并不在上述操作的依赖路径上，因为并不会主动完成，也就是说，在训练时mean_update和variance_update并不会被使用到，其值一直是初始值。因此在测试阶段(training=False)使用这两个作为mean和variance并进行归一化操作，这样就会出现错误。而如果使用tf.control_dependencies函数，会在训练阶段每次训练操作执行前被动地去执行mean_update和variance_update，因此moving_mean和moving_variance会被不断更新，在测试时使用该参数也就不会出现错误。