神经网络

最新推荐文章于 2022-06-16 12:16:57 发布

snoowood

最新推荐文章于 2022-06-16 12:16:57 发布

阅读量1.4k

点赞数 1

分类专栏：机器学习文章标签：机器学习神经网络 neural networks

本文链接：https://blog.csdn.net/l01w29/article/details/19996405

版权

机器学习专栏收录该内容

4 篇文章 0 订阅

订阅专栏

1. 神经细胞

神经元，又称神经细胞，是构成神经系统结构和功能的基本单位。神经元是具有长突触(轴突)的细胞，它由细胞体和细胞突起构成。细胞突起是由细胞体延伸出来的细长部分，又可分为树突和轴突。每个神经元可以有一或多个树突，可以接受刺激并将兴奋传入细胞体。每个神经元只有一个轴突，可以把兴奋从胞体传送到另一个神经元。如下图所示

我们已经知道，神经元把所有从树突进来的信号进行叠加处理（并不是简单的相加），如果叠加结果超过某个阈值，就会激发神经元进入兴奋状态，这时就会有一个电信号经过轴突传向其它神经元。如果叠加结果没有超过这个阈值，就不会有电信号产生。（当然神经元的真实反应要比上面的描述复杂得多）

2. 人工神经细胞

了解了神经细胞的工作原理，我们可以构造一个有n个输入（ $x_{1}, x_{2}, ..., x_{n}$ ）的人工神经细胞（以下简称神经细胞）

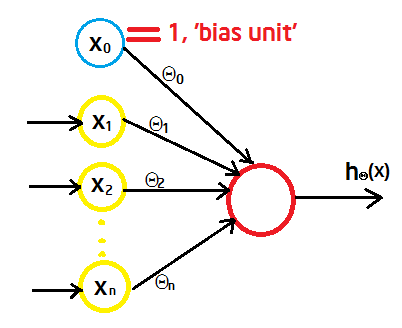
假设这n条到神经细胞体的输入边的权重分别为（ $\Theta_{1}, \Theta_{2}, ..., \Theta_{n}$ ），我们再为神经细胞增加一个边权重为 $\Theta_{0}$ 的输入 $x_{0}$ （叫做bias unit），且始终有 $x_{0}$ = 1（这里可以把 $\Theta_{0}x_{0}$ 的值想像成神经细胞的阈值）。则神经细胞的输出

$h_{\mathbf{\Theta}}(\mathbf{x}) = \frac{1}{1+e^{-\mathbf{\Theta }^{T}X}}$

其中

$\mathbf{\Theta } = \begin{pmatrix} \\ \Theta _{0} \\ \Theta _{1} \\ \Theta _{2} \\ ... \\ \Theta _{n} \end{pmatrix}$ ， $\mathbf{X} = \begin{pmatrix} x_{0}\\ x_{1}\\ x_{2}\\ ...\\ x_{n}\\ \end{pmatrix}$

3. 人工神经网络

已经了解了神经细胞的结构，下面我们可以构造一个4层K类的人工神经网络（以下简称神经网络）

其中第1层是输入层，输入是样例的特征；最后一层是输出层，表示神经网络选择某一类别的几率，和Logistic Regression类似，我们选择几率最大的输出代表类别；介于输入层和输出层之间的是隐藏层，隐藏层通常由1到多层组成，当然也可以没有。注意到除了输出层，我们在每一层都增加了一个'bias unit‘，其值为1，它的作用我们在上一节讲过。我们用

L表示神经网络总的层数

$a_{j}^{(i)}$ 表示第i层第j个神经细胞的激励值，即第i层第j个神经细胞的输出

$s_{i}$ 表示第i层神经细胞的数量（不包括bias unit）

$\mathbf{\Theta}_{p, q}^{(i)}$ 表示第i层第q个神经细胞到第i+1层第p个神经细胞的边的权重

$\mathbf{\Theta}^{(i)}$ 表示第i层神经细胞到第i+1层神经细胞的所有边的权重的矩阵， $\mathbf{\Theta}^{(i)}$ 是一个 $s_{i+1}\times (s_{i}+1)$ 的矩阵

则有

$a_{j}^{(i+1)} = g(z^{(i+1)}) = g(a_{0}^{(i)}\mathbf{\Theta }_{j,0}^{(i)}+a_{1}^{(i)}\mathbf{\Theta }_{j,1}^{(i)}+...+a_{s_{i}}^{(i)}\mathbf{\Theta }_{j,s_{i}}^{(i)})$ ，其中 $z^{(i+1)} = a_{0}^{(i)}\mathbf{\Theta }_{j,0}^{(i)}+a_{1}^{(i)}\mathbf{\Theta }_{j,1}^{(i)}+...+a_{s_{i}}^{(i)}\mathbf{\Theta }_{j,s_{i}}^{(i)}$

$g(x)$ 为Sigmoid函数。如果使用矩阵的形式，则有

$\begin{pmatrix} a_{1}^{(i+1)}\\ a_{2}^{(i+1)}\\ ...\\ a_{s_{i+1}}^{(i+1)} \end{pmatrix} = \mathbf{\Theta }^{i}\begin{pmatrix} a_{0}^{(i)}\\ a_{1}^{(i)}\\ ...\\ a_{s_{i}}^{(i)}\\ \end{pmatrix}$

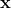这样逐层向前，我们最终可以计算得到输出层K个神经细胞的输出 $\mathbf{y} = \begin{pmatrix} h_\mathbf{\Theta}^{(1)}(\mathbf{x})\\ h_\mathbf{\Theta}^{(2)}(\mathbf{x})\\ ...\\ h_\mathbf{\Theta}^{(K)}(\mathbf{x})\\ \end{pmatrix}$ ，假设 $h_\mathbf{\Theta}^{(i)}(\mathbf{x})$ 最大，则i即为输入 $\mathbf{x}$ 的类别。这个过程叫做Forward Propagation。

4. 训练神经网络

前面讲了怎样使用神经网络进行分类，在能得到正确的结果前，我们还需要还对神经网络进行训练。假设有K个类别，则神经网络的输出 $\mathbf{y}\in \mathbb{R}^{(K)}$ ；有一个样例 $(\mathbf{x}^{(i)},\mathbf{y}^{(i)})$ ，同样的 $\mathbf{y}^{(i)}\in \mathbb{R}^{(K)}$ ，其中 $\mathbf{y}^{(i)}_{j}=1$ 表示 $\mathbf{x}^{(i)}$ 属于第j个类别。比如，K=5， $\mathbf{x}^{(i)}$ 属于类别3，则有 $\mathbf{y}^{(i)}=\begin{pmatrix} 0\\ 0\\ 1\\ 0\\ 0 \end{pmatrix}$ 。

假设神经网络的输出为 $\mathbf{y} = \begin{pmatrix} h_\mathbf{\Theta}^{(1)}(\mathbf{x})\\ h_\mathbf{\Theta}^{(2)}(\mathbf{x})\\ ...\\ h_\mathbf{\Theta}^{(K)}(\mathbf{x})\\ \end{pmatrix}$ ，

定义其Cost Function为

$J\left ( \mathbf{\Theta } \right )=-\frac{1}{m}\sum_{i=1}^{m} \sum_{k=1}^{K}[\mathbf{y}_{k}^{(i)}log(h_{\mathbf{\Theta }}(\mathbf{x}^{(i)}))_{k} + (1-\mathbf{y}_{k}^{(i)})log(1-{\color{Blue} }h_{\mathbf{\Theta }}(\mathbf{x}^{(i)}))_{k})]$

$+\frac{\lambda }{2m}\sum_{l=1}^{L}\sum_{i=1}^{s_{l}}\sum_{j=1}^{s_{l+1}}(\mathbf{\Theta }_{j,i}^{(l)})^{2}$

下面我们介绍一下Back Propagation（反射传播）算法：

令 $\Delta_{ij}^{(l)} = 0, ( l=1 \to L, i=0 \to s_{l+1}, j=0 \to s_{l} )$

for p = 1 to m

令 $a^{(1)} = \mathbf{x}^{(p)}$

使用forward propagation计算 $z^{(2)}, z^{(3)}, ..., z^{(L)}$ ； $a^{(2)}, a^{(3)}, ..., a^{(L)}$ ；其中 $z^{(i+1)} = \mathbf{\Theta } ^{(i)}a^{(i)}$ ， $a^{(i+1)} = g(z^{(i+1)})$

计算 $\delta ^{(L)} = a^{(L)} - \mathbf{y}^{(p)}$

计算 $\delta ^{(L-1)},\delta ^{(L-2)},...,\delta ^{(2)}$ ，其中 $\delta ^{(i)} = (\mathbf{\Theta}^{(i)})^{T}*\delta ^{(i+1)}.*{g}'(z^{(i)})$ ，注意 $\delta ^{(i+1)}$ 不包括 $\delta _{0}^{(i+1)}$ ，因为每一层的第一个细胞都没有输入

更新 $\Delta _{ij}^{(l)} = \Delta _{ij}^{(l)} + a_j^{(l)}\delta _i^{(l+1)},(l=1 \to L-1,i=0\to s_{l+1}, j=0 \to s_l)$

$\left\{\begin{matrix} D _{ij}^{(l)} = \frac{1}{m}\Delta _{ij}^{(l)} & if &j=0 \\ D _{ij}^{(l)} = \frac{1}{m}\Delta _{ij}^{(l)}+\lambda \mathbf{\Theta }_{ij}^{(l)} & if &j\neq 0 \end{matrix}\right.\left.\begin{matrix} \\ \end{matrix}\right|\frac{\partial }{\partial \mathbf{\Theta }_{ij}^{(l)}}J(\mathbf{\Theta }) = D _{ij}^{(l)}$

－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－

补充一点： ${g}'(x)=g(x)*(1-g(x))$ ，它的推导比较简单，这里不再给出。

Back Propagation只是计算了 $\frac{\partial }{\partial \mathbf{\Theta }_{ij}^{(l)}}J(\mathbf{\Theta })$ ，后面可以使用Gradient Descent对 $\mathbf{\Theta }$ 进行更新，直到 $\mathbf{\Theta }$ 收敛。