1. 正交(Orthogonality)
如果两个向量
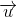 和
和
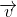 的内积为0,我们说向量
的内积为0,我们说向量
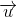 和
和
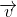 正交。在二维平面中,两个向量正交就是它们的夹角为
正交。在二维平面中,两个向量正交就是它们的夹角为
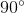 。
。
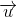 和
和
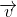 的内积为0,我们说向量
的内积为0,我们说向量
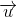 和
和
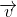 正交。在二维平面中,两个向量正交就是它们的夹角为
正交。在二维平面中,两个向量正交就是它们的夹角为
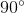 。
。
如果矩阵
 满足
满足
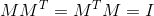 ,其中
,其中
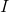 是单位矩阵,则
是单位矩阵,则
 是正交矩阵。
是正交矩阵。
 满足
满足
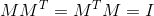 ,其中
,其中
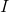 是单位矩阵,则
是单位矩阵,则
 是正交矩阵。
是正交矩阵。
若
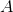 是正交矩阵,则有:
是正交矩阵,则有:
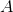 是正交矩阵,则有:
是正交矩阵,则有:
是正交矩阵;
的各行是单位向量且两两正交;
的各列是单位向量且两两正交;
;
- 若
是正交矩阵,则
也是正交矩阵;
2. 线性变换(Linear Transformation)
我们有一个对角矩阵
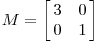
考虑平面上任意一点(x, y)经
 线性变换后得到新的点
线性变换后得到新的点
 线性变换后得到新的点
线性变换后得到新的点
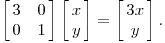
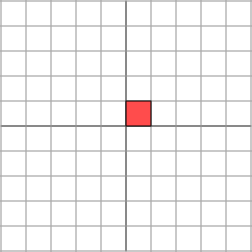
变换后的效果如下图所示,平面在水平方向上被拉伸了3倍,在垂直方向没有改变:
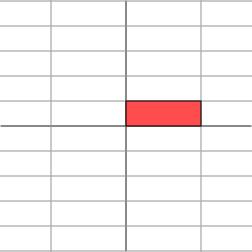
当
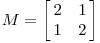
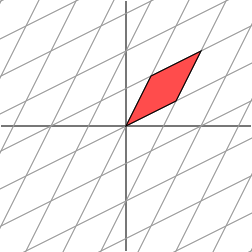
时,变换效果如下

如果我们将第1个网络旋转
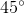 ,再做相同的线性变换,会有下面的效果
,再做相同的线性变换,会有下面的效果
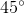 ,再做相同的线性变换,会有下面的效果
,再做相同的线性变换,会有下面的效果
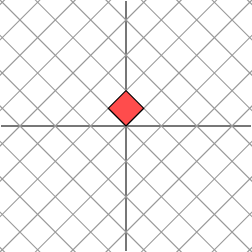
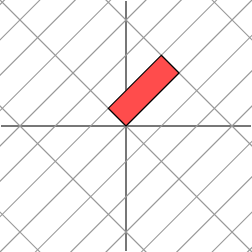
我们发现,旋转后的网格与原来的网格发生了相同的变化,都是在一个方向上拉伸了3倍。
上面的例子比较特殊,因为
 是一个2x2的对称矩阵。事实上,对于任意的2x2的对称矩阵
是一个2x2的对称矩阵。事实上,对于任意的2x2的对称矩阵
 ,我们都可以通过把原始的网格旋转一定的角度,然后通过
,我们都可以通过把原始的网格旋转一定的角度,然后通过
 做一个线性变换后,使其表现为一个方向或两个正交的方向上产生拉伸。
做一个线性变换后,使其表现为一个方向或两个正交的方向上产生拉伸。
 是一个2x2的对称矩阵。事实上,对于任意的2x2的对称矩阵
是一个2x2的对称矩阵。事实上,对于任意的2x2的对称矩阵
 ,我们都可以通过把原始的网格旋转一定的角度,然后通过
,我们都可以通过把原始的网格旋转一定的角度,然后通过
 做一个线性变换后,使其表现为一个方向或两个正交的方向上产生拉伸。
做一个线性变换后,使其表现为一个方向或两个正交的方向上产生拉伸。
3. 特征值分解
更一般的,对于方阵
 ,如果存在标量
,如果存在标量
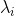 和非零列向量
和非零列向量
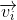 ,使得
,使得
 ,如果存在标量
,如果存在标量
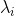 和非零列向量
和非零列向量
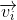 ,使得
,使得
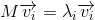
则称向量
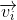 是方阵
是方阵
 的特征向量(eigenvector),而把
的特征向量(eigenvector),而把
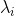 叫做方阵
叫做方阵
 的特征值(eigenvalue)。从几何学的角度讲,上式表示向量
的特征值(eigenvalue)。从几何学的角度讲,上式表示向量
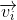 在使用矩阵
在使用矩阵
 进行变换后,只是发生了拉伸或收缩,而方向并没有改变。我们对上式做一个变换,可以得到
进行变换后,只是发生了拉伸或收缩,而方向并没有改变。我们对上式做一个变换,可以得到
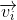 是方阵
是方阵
 的特征向量(eigenvector),而把
的特征向量(eigenvector),而把
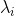 叫做方阵
叫做方阵
 的特征值(eigenvalue)。从几何学的角度讲,上式表示向量
的特征值(eigenvalue)。从几何学的角度讲,上式表示向量
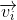 在使用矩阵
在使用矩阵
 进行变换后,只是发生了拉伸或收缩,而方向并没有改变。我们对上式做一个变换,可以得到
进行变换后,只是发生了拉伸或收缩,而方向并没有改变。我们对上式做一个变换,可以得到
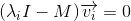
我们如果把
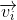 看作变量,则上式有非零解的充要条件是
看作变量,则上式有非零解的充要条件是
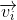 看作变量,则上式有非零解的充要条件是
看作变量,则上式有非零解的充要条件是
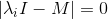
通过解上述方程,可以得到方阵M的特征向量和特征值。
4. 奇异值分解
先看一个简单的例子,假设向量
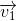 和
和
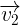 是两个正交的单位向量,则
是两个正交的单位向量,则
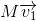 和
和
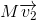 也正交
也正交
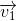 和
和
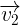 是两个正交的单位向量,则
是两个正交的单位向量,则
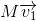 和
和
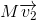 也正交
也正交
:
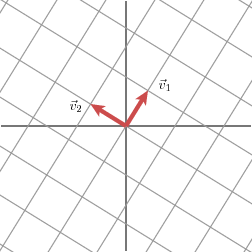
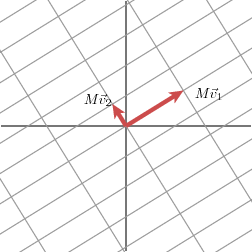


我们用向量
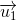 和
和
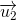 分别表示沿向量
分别表示沿向量
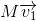 和
和
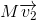 方向的单位向量;
方向的单位向量;
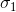 和
和
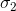 分别表示向量
分别表示向量
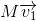 和
和
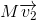 的长度,则
的长度,则
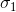 和
和
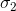 分别分别描述了网格沿某个特定方向拉伸或收缩的数量,我们把
分别分别描述了网格沿某个特定方向拉伸或收缩的数量,我们把
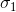 和
和
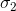 叫做矩阵
叫做矩阵
 的奇异值(singular value)。因此我们有
的奇异值(singular value)。因此我们有
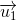 和
和
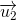 分别表示沿向量
分别表示沿向量
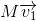 和
和
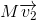 方向的单位向量;
方向的单位向量;
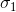 和
和
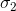 分别表示向量
分别表示向量
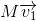 和
和
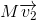 的长度,则
的长度,则
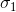 和
和
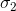 分别分别描述了网格沿某个特定方向拉伸或收缩的数量,我们把
分别分别描述了网格沿某个特定方向拉伸或收缩的数量,我们把
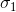 和
和
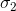 叫做矩阵
叫做矩阵
 的奇异值(singular value)。因此我们有
的奇异值(singular value)。因此我们有
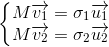
对于任意向量
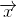 ,由于
,由于
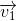 和
和
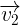 正交,可以得到
正交,可以得到
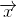 ,由于
,由于
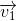 和
和
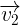 正交,可以得到
正交,可以得到
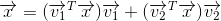
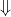
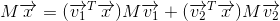
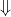
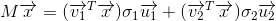
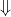
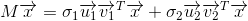
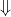
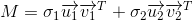
通常把
 表示为
表示为
 表示为
表示为
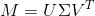
其中
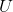 的列向量是
的列向量是
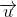 ;
;
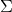 是对角矩阵,对角线上的每一项分别是
是对角矩阵,对角线上的每一项分别是
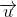 对应的
对应的
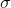 ;
;
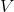 的列向量是
的列向量是
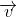 。可以看到,奇异值分解把矩阵M分解为三个部分,
。可以看到,奇异值分解把矩阵M分解为三个部分,
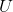 表示目标域中的一组正交基,
表示目标域中的一组正交基,
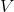 表示原始域中的一组正交基,
表示原始域中的一组正交基,
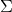 描述了
描述了
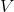 中的一组向量变换为
中的一组向量变换为
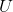 中的向量时拉伸或收缩的数量。
中的向量时拉伸或收缩的数量。
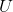 的列向量是
的列向量是
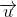 ;
;
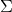 是对角矩阵,对角线上的每一项分别是
是对角矩阵,对角线上的每一项分别是
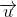 对应的
对应的
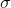 ;
;
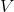 的列向量是
的列向量是
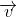 。可以看到,奇异值分解把矩阵M分解为三个部分,
。可以看到,奇异值分解把矩阵M分解为三个部分,
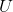 表示目标域中的一组正交基,
表示目标域中的一组正交基,
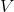 表示原始域中的一组正交基,
表示原始域中的一组正交基,
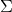 描述了
描述了
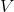 中的一组向量变换为
中的一组向量变换为
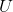 中的向量时拉伸或收缩的数量。
中的向量时拉伸或收缩的数量。
参考:






















 568
568

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








