基于张量网络的机器学习（一）

在这篇文章里，我会对前面所提到过的张量进行一定的拓展！

张量

如果你是第一次看到这个名词，可能首先会想到张力，毕竟高中物理肯定曾告诉你，

   张力是物体受到拉力作用时，存在于其内部而垂直于两个相邻邻部分接触面上的相互牵引力。

显然张力是一个物理量，那这和张量又有什么关系？张量很便于表达各种物理量！我看了一些关于张量的文章，有关于科普的，也有较为数学化的，我认为我最大的收获就是：相比前面文章的万物皆可傅里叶（通过傅里叶变换画出图像，具体怎么画的其实还不太懂，想要多了解这方面的知识的可以进入下面链接瞧一瞧），张量带给我的认知便是万物皆可张量。
万物皆可傅里叶！

一.张量怎么让钱缩水的?

首先让我们回顾一下高中曾学习过的知识。

1.基向量

在我们的认知中，向量是一个包含了大小和方向信息的量，而基向量顾名思义就是表示其他向量的基础构件。在我们所接触的空间直角坐标系下，通常情况下三个相互正交的基向量分别是：$\vec{i}$= $(1,0,0)$ ,$\vec{j}$= $(0,1,0)$,$\vec{k}$= $(0,0,1)$

到了这里，再去看三个及以上非正交的大小不一定为1的基向量就很好理解了。

2.分量

现在，我们找到一组基向量$\vec{i}$，$\vec{j}$，$\vec{k}$,则一个向量$\vec{a}$= $(3,4,0)$=3$\vec{i}$+4$\vec{j}$+0$\vec{k}$，3、4、0就是$\vec{a}$在各自基向量下的分量。

3.张量让钱缩水和增值的神奇功能

现在网上流传着两种“高级”的数学题，一种是这样的：

另一种是这样的：

   为了不让我的钱包缩水，我决定小小的证明一下第一个命题的错误。
   对于这个命题，小学生都可以很清楚的知道问题出在单位（量纲）上，而更加本质的却是张量。现在，我们把这元、角、分三个金额，并将他们作为基画在一条直线上（这三种金额本质是在一维线性空间的基）


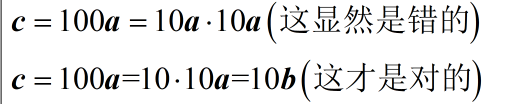
所以我可怜的钱包并不会莫名其妙的缩水！至于为什么会这样，请细细琢磨下面这句话。

张量所描述的物理量是不随观察者或者说参考系而变化的，当参考系变化时（其实就是基向量变化）

你品，你细品！

---

二.回到张量开始的地方

   张量这一术语起源于力学，它最初是用来表示弹性介质中各点应力状态的，后来张量理论发展成
为力学和物理学的一个有力的数学工具。张量之所以重要，在于它可以满足一切物理定律必须与坐标
系的选择无关的特性。张量是一个可用来表示在一些矢量、标量和其他张量之间的线性关系的多线性
函数。

   物体由于外因（受力、湿度、温度场变化等）而变形时，在物体内各部分之间产生相互作用的内
力，以抵抗这种外因的作用，并试图使物体从变形后的位置恢复到变形前的位置。在所考察的截面某
一点单位面积上的内力称为应力。同截面垂直的称为正应力或法向应力，同截面相切的称为剪应力或
切应力。

现在，我们面前有一根钢梁，并在其内部任取一个点，图是这样的：

然后我们对这根钢梁进行切割并以该点为原点建立空间直角坐标系：

那么我们如何描述在该点所有方向上的应力状态呢？

   可以注意到，每一个量都有两个下标，第一个下标代表截面的法线方向，第二个下标代表做功的方向，其中 p_xx，p_yy，p_zz为相应截面的正应力，其他的力都为相应截面的切应力，（对于第二个下标相同的分量，是不能合并起来表示的，毕竟力的来源是不同的，比如说我们曾接触过的作用力和反作用力）然后我们可以得到一个二阶张量：

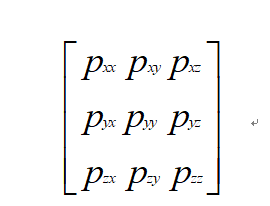
   上面共有9个分量，每一个分量里含有两个基向量的信息（相当于两个基组成了一个新基），所以这是一个二阶张量，那么相应的，如果一个分量里具有n个基向量的信息（如果是在三维下，能够拥有3ⁿ个分量），那得来的新张量就是一个n阶的张量了。
   在日常生活中，即便是标量都可以用0阶张量来表示，那么对于蕴含着更多信息的物理量，对于一个初学者来说，我很愿意去相信现实生活中的一切物理量都是可以借助张量来表示，那不就是万物皆可张量吗，但是很遗憾的是，很多的物理量（比如工程应变）是不可以通过张量来描述的，但即便如此，张量强大的表示能力又不会随着观察者（坐标系）不同而变化，能够有效的表示宇宙的万物。
   而对于前面所讲过的那个想让我钱包缩水的古怪问题，我跟倾向于这样的解释：一个一阶张量不能分解成两个一阶张量的乘积。那么同样的，同阶张量也不能分解成同阶张量的乘积。

三.张量的基础知识

到了这里，我才开始去搭一栋楼的地基，好吧，我不是土木工程师，但是我的一个高中同学以后没准就会是一个很会打地基的土木工程师。

1.张量的定义

• 张量是多维数组，这个定义和图像视频的原理牵扯很深；
• 张量是某种几何对象，不会随基的改变而改变，就像是“横看成岭侧成峰，远近高低各不同”，它的本来面目不会变。
• 张量是多重线性映射，对于一个映射$\Phi$，若：
  
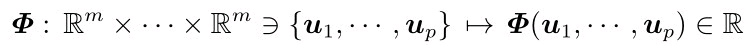
  满足对第i个变量的线性性，即
  
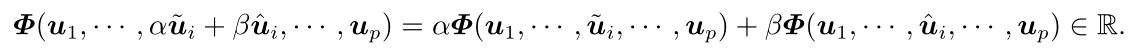
  映射$\Phi$对p个变量具有线性性，则该映射就称为p阶张量或p重线性函数。

现在，这里有一张图，可能能够帮助你理解张量：

   在m维空间的n阶张量具有mⁿ个分量，另外，上图可能会让你陷入一个误区，二阶张量可以由矩阵表示，但是矩阵并不等于张量，张量蕴含的信息（大小和）要比简单的矩阵蕴含的更多，相信看过前面内容的你能够明白这点。

2.爱因斯坦标记法

   其实我真的很讨厌这些符号，我经常读不准这些怪异的希腊字母的读音，但是，想到了如果在对张量进行一些变换时，如果不用这些符号，可能我的笔芯有点撑不住，所以，我有必要讲述一下爱因斯坦标记法。

   在数学里，特别是将线性代数套用到物理时，爱因斯坦求和约定是一种标记的约定，又称为爱因
斯坦标记法，在处理关于坐标的方程式时非常有用。这约定是由阿尔伯特·爱因斯坦于1916年提出的。
后来，爱因斯坦与友人半开玩笑地说：“这是数学史上的一大发现，若不信的话，可以试着返回那不
使用这方法的古板日子。”

现在有一个线性方程组：

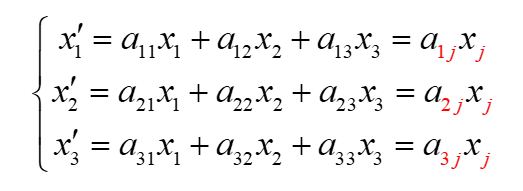
如果使用爱因斯坦标记法，我们可以得到：

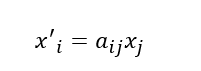
简单吧！其中等号右边的一项里只出现一次的i是自由指标，出现了两次的j是哑指标，再来一个例子：

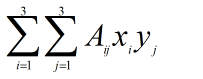
如果使用爱因斯坦标记法，我们可以得到：

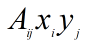
因此聪明的你已经可以发现：
1.哑指标就是表示要把该项在该指标的取值范围内遍历求和；
2.自由指标在每一项中只出现一次，一个公式中必须相同；
3.凡是遇到求和符号下界字母和同项下标相同的情况，则需要去掉求和符号；
4.如果你是个程序员，可以很清晰的看出，哑指标相当于求内层循环，自由指标相当于求外层循环。
5.哑指标和自由指标都有范围，然后就又有了一个规定：如果不标明取值范围，则拉丁指标 i, j, k, …表示三维指标，取值1, 2, 3；希腊指标$\alpha$,$\beta$,$\gamma$…均为二维指标，取值1, 2。

3.偏导数的下标记法

   我们有时候会发现在弹性力学中也有一种标记的约定，名为逗号约定，用于当分量为偏导数的情况。
   逗号约定：为了缩写含有一对直角坐标x_i取偏导数的表达式，我们规定当逗号后面紧跟一个下标i时，表示某物理量对x_i求偏导数。

意思很简单，比如：

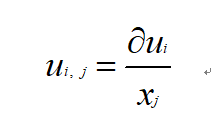
到这里也就为止了，还想了解多一点偏导数的下标记法可以进入下面这个链接看一看：
张量的定义

4.特殊的张量符号

• 克罗内克符号$\delta$_ij
  
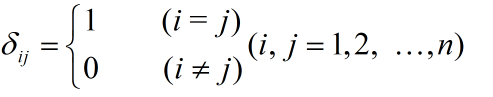
  在一个三维空间里，$\delta$_ij的分量集合为一个单位矩阵，见下图：
  
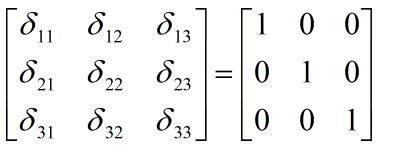
  $\delta$_ij还具有一个很重要的换标作用，比如：
  
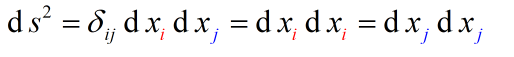
  如果符号 $\delta$ 的两个指标中，有一个和同项中其它因子的指标相重，则可以把该因子的那个重指标换成 $\delta$ 的另一个指标，而 $\delta$ 自动消失。
• 置换符号e_rst
  
  那么显然会有下面这种情况：
  

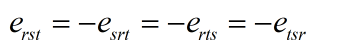
5.张量的运算

• 相等
  若两个张量 T=T_ij$\vec{e}$_i$\vec{e}$_j，S=S_ij$\vec{e}$_i$\vec{e}$_j相等，则对应分量T_ij=S_ij

• 和差
  若两个同阶张量 T=T_ij$\vec{e}$_i$\vec{e}$_j，S=S_ij$\vec{e}$_i$\vec{e}$_j之和或差为另一个同阶张量 A=A_ij$\vec{e}$_i$\vec{e}$_j，
  则分量关系为A_ij=T_ij$\pm$S_ij

• 数积
  一个张量 A=A_ij$\vec{e}$_i$\vec{e}$_j和一个数$\lambda$相乘得到另一个张量 B=B_ij$\vec{e}$_i$\vec{e}$_j，则 B_ij=$\lambda$A_ij

• 并积
  两个同维张量 T=T_ijk$\vec{e}$_i$\vec{e}$_j$\vec{e}$_k，S=S_lm$\vec{e}$_l$\vec{e}$_m的并积 A 是一个同维但阶数为两个张量阶数之和的新张量，则 A =T S=A_ijklm$\vec{e}$_i$\vec{e}$_j$\vec{e}$_k$\vec{e}$_l$\vec{e}$_m，对应分量关系为A_ijklm=T_ijkS_lm

• 缩并
  若对基张量（基矢量的张量积）中的任意两个基矢量求点积，张量将缩并为低二阶的新张量。比如新张量 S=T_ijk ( $\vec{e}$_i $\cdot$ $\vec{e}$_j)$\vec{e}$_k= T_ijk$\delta$_ij$\vec{e}$_k=T_iik$\vec{e}$_j=S_j$\vec{e}$_j，分量关系为：T_iik=S_k

• 内积
  并积加缩并为内积。

• 点积
  前张量 A 的最后基矢量与后张量 B 的第一基矢量缩并的结果。

• 双点积
  对前、后张量中两对近挨着的基矢量缩并的结果称为双点积，但是由于下标的顺序问题，从而出现了两种双点积，一种叫并双点积，另一种叫串双点积。

• 并矢
  把 K 个独立矢量并写在一起称为并矢量，它们的并积是一个 K 阶张量。
  
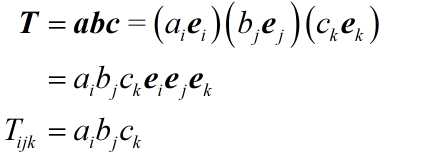
  并矢量中各矢量的顺序不得任意调换。

张量的运算规则很多，但只要记住两点即可万变不离其宗:
1.克罗内克符号的换标作用；
2.基矢量的顺序不得随意改变。

6.张量的三种记法（补充）

可以注意到张量的分量记法和克罗内克符号很类似，但是两者并不是一样的。

四.张量的应用

1.表达万物

   其实看过前面的内容就可以知道，张量可以拿来表示许多量，从标量到矢量，再到更加复杂的量，张量的各种符号使得张量能更简洁地表达一系列复杂的推导过程，当然，再复杂的就暂时不在我的了解范围之内了，我只需要知道张量的这种用途就好了

2.存储信息

   张量是现代机器学习的基础。它的核心是一个数据容器，顾名思义张量可以用来存储信息。相信现在的你已经对张量有了一定程度的了解，现在开始这篇文章的最后一个内容：

   也许你还有点没看懂，那还记得前面张量的定义中提到的张量是多维数组吗？这样你就能够稍微理解上面这张图所展示的内容了。
   对于一段数据，当时间（对这段数据很重要时，应该将数据存储在带有时间轴timesteps）的3D张量中每个样本（sample）可以被编码为一个向量序列（即2D张量），因此一个数据批量就被编码为一个3D张量，比如股票价格的数据集；

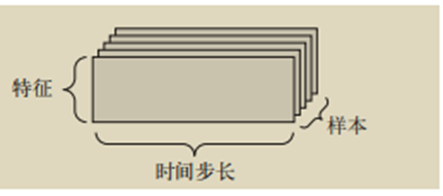
   图像一般具有三个维度，可以存储在3D张量里；
   4D张量则可以存储一个图片集；

   5D张量可以用来存储视频数据。
因为自知掌握的这方面的知识还不够深，也就不便献丑，所以下面顺便附上一篇写了关于这方面知识的文章：
张量的通俗理解!这方面讲的很详细