分析
复健,一题回溯。
与其他的二染色不同,本题需要穷尽所有可能,求其最多可染黑多少个点。
思路
对第i个点
如果i>V,是一个虚点,表示所有点已经探测完毕
比较染点个数,保存结果
如果i<V,是一个实点
遍历该点的所有路
如果相邻的点未染色,则染色并进入第i+1个点
将第i个点不染色(如过相邻的点染色也表示不染色),并进入第i+1个点
代码
#include <cstdio>
#include <cstring>
#define MAX_V 105
int G[MAX_V][MAX_V];
int V, E, max;
int color[MAX_V], r[MAX_V];
void dfs(int v, int s)
{
if (v > V) {
if (s > max) {
max = s;
for (int i = 1; i <= V; i++)
r[i] = color[i];
}
return;
}
bool flag = true;
for (int i = 1; i <= V; i++)
if (G[v][i] && color[i]) {
flag = false;
break;
}
if (flag) { color[v] = 1; dfs(v+1, s+1); }
color[v] = 0; dfs(v+1, s);
}
void solve()
{
memset(color, 0, sizeof(color));
max = 0;
dfs(1, 0);
printf("%d\n", max);
for (int i = 1, j = 1; i <= V; i++)
if (r[i]) {
printf("%d", i);
if (j++ != max) printf(" ");
}
printf("\n");
}
int main()
{
int T;
scanf("%d", &T);
while (T--) {
scanf("%d %d", &V, &E);
memset(G, 0, sizeof(G));
for (int i = 0; i < E; i++) {
int v1, v2;
scanf("%d%d", &v1, &v2);
G[v1][v2] = 1; G[v2][v1] = 1;
}
solve();
}
return 0;
}题目
Description
You are to write a program that tries to find an optimal coloring for a given graph. Colors are applied to the nodes of the graph and the only available colors are black and white. The coloring of the graph is called optimal if a maximum of nodes is black. The coloring is restricted by the rule that no two connected nodes may be black.
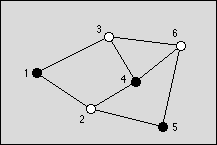
Figure: An optimal graph with three black nodes
Input and Output
The graph is given as a set of nodes denoted by numbers 1...n,n≤100 , and a set of undirected edges denoted by pairs of node numbers (n1,n2),n1≠n2 . The input file contains m graphs. The number m is given on the first line. The first line of each graph contains n and k, the number of nodes and the number of edges, respectively. The following k lines contain the edges given by a pair of node numbers, which are separated by a space.
The output should consists of 2 m lines, two lines for each graph found in the input file. The first line of should contain the maximum number of nodes that can be colored black in the graph. The second line should contain one possible optimal coloring. It is given by the list of black nodes, separated by a blank.
Sample Input
2
6 8
1 2
1 3
2 4
2 5
3 4
3 6
4 6
5 6
12 11
1 2
3 1
4 1
5 1
6 1
7 1
8 2
9 2
10 2
11 2
12 2
Sample Output
3
1 4 5
10
3 4 5 6 7 8 9 10 11 12







 本文深入分析了图论中一个关于最优着色的问题,通过详细解析算法逻辑和代码实现,旨在找到最多可染黑的点数。文中包括算法思路、代码实现以及实例解析,为读者提供了一个全面理解复杂图论问题解决方法的视角。
本文深入分析了图论中一个关于最优着色的问题,通过详细解析算法逻辑和代码实现,旨在找到最多可染黑的点数。文中包括算法思路、代码实现以及实例解析,为读者提供了一个全面理解复杂图论问题解决方法的视角。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








