关于PID的几种整定方法

作者：吴 宇 航

一、ZN整定法

       1.1、阶跃响应法（开环法）

       1.2、等幅振荡法（闭环法）

二、衰减振荡法

一、ZN整定法

ZN整定法适用于串联型PID公式如公式1和理想型PID公式如公式2

公式 1

公式 2

两种公式需根据项目的自身条件选定，理想型公式的Kp比例增益会大于串联型公式的Kp。且ZN整定法另一限制是被控对象的系统特征要能够用一阶时滞系统近似表达，如温度模型就是典型的一阶时滞系统。

ZN整定法有此限制的原因是因为其并不是通过理论分析推导而出，而是他们根据大量实验数据总结归纳出来的。

1.1、阶跃响应法（开环法）

图1为阶跃响应法的公式

图 1

纯比例控制采用第一行公式，比例加积分控制采用第二行公式，比例加积分和微分控制采用第三行公式。

接下来以加热温度的PID控制为例，讲解其公式的使用。

首先我们以一个恒定加热功率M加热其温度达到稳态，得到如图2的一条曲线：

图 2

图中L 为控制器响应时间，T为被控对象从初始值到达稳态的时间系数。

L和T我们都可从图中直接得出而K则需要通过计算得出，在计算中我们应用到最小--最大归一法，先将加热功率归一化（加热功率M-最小加热功率）/（最大加热功率-最小加热功率）得到比例a，再将温度归一化（稳态温度-最小温度）/（最大温度-最小温度）得到比例b，将a/b得到K。

接着将K、T、L带入公式中就可求出Kp、Ti、Td。

1.2、等幅振荡法（闭环法）

等幅振荡法是ZN整定的第二种方法，其为闭环控制方法。还是以加热温度为例，但与阶跃响应法不同的是临界震荡法需要采用纯比例控制器，如图3:

图 3

纯比例控制会让曲线出现稳态误差，继续增大Kp会让曲线出现振荡如图4：

图 4

而我们就是要继续增大Kp让曲线出现等幅振荡，既不能是发散如图5，也不能是收敛如图6：

图 5

图 6

要出现如图7的等幅振荡，所以这种方法被称之为等幅振荡法。

图 7

在增大Kp时应注意Kp的大小，要一点一点往上加，因为一不小心就会出现发散的趋势很容易把系统搞坏，这个方法用起来是不那么安全的。

我们以一个实际曲线为例如图8：

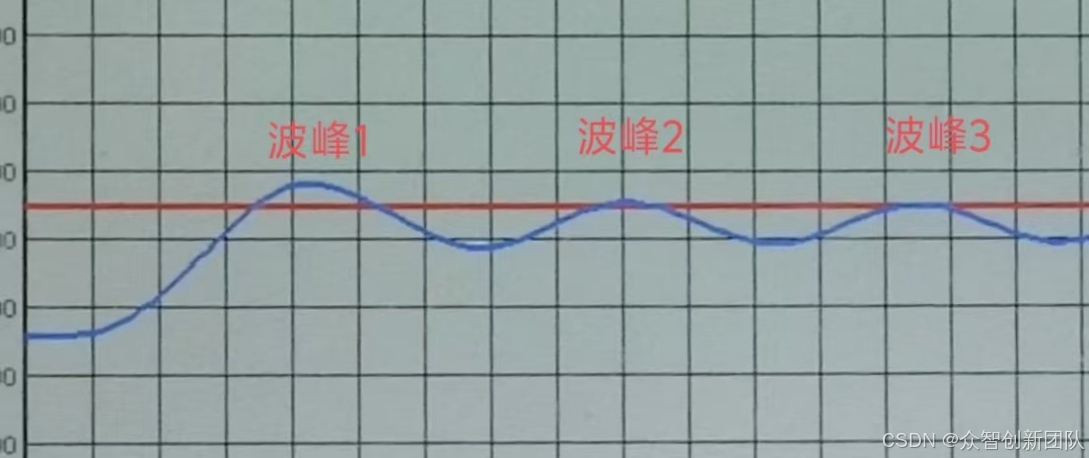
图 8

理论上我们要取波峰1和波峰2的时间间隔，但实际波形并不是完全等幅的，第一个波峰与后面的波峰并不相等，是稍微高一点的，那我们就转为取波峰2和波峰3的时间间隔。波峰2的时间是618，波峰3的时间是924，相减得出周期为314，该曲线的比例增益Kp为16。

图9为等幅振荡法的参数公式：

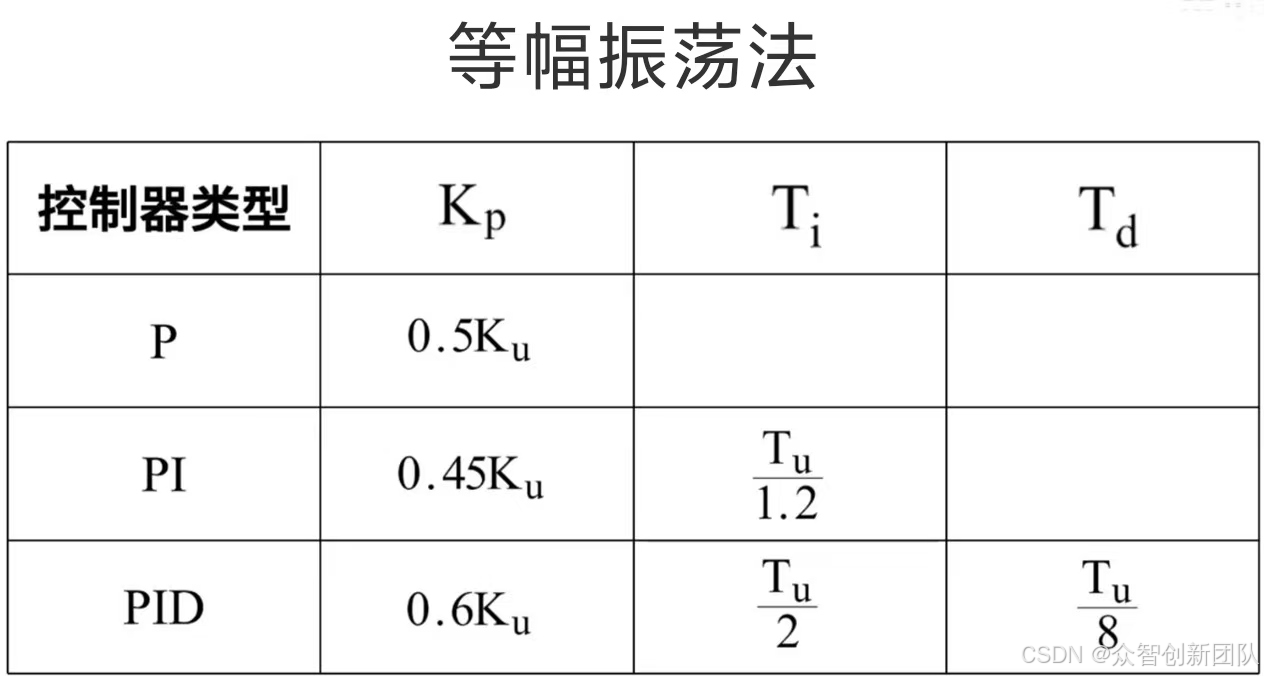
图 9

纯比例控制采用第一行公式，比例加积分控制采用第二行公式，比例加积分和微分控制采用第三行公式。

以PID控制为例，公式中的Ku就是该曲线等幅振荡的Kp值，所以PID控制的Kp就是16*0.6=9.6，Tu就是两个峰值的时间相减的周期，所以Ti就是314/2=157，Tu就是314/8=39.25,这里的时间单位是与采样周期一致。

等幅振荡法的计算步骤是比较简洁的，相比于阶跃响应法的计算，其既不需要做切线，也不用计算交点和归一化处理，唯一费点时间的就是要试出能让曲线等幅振荡的比例增益。

图10为参数的实际测试图：

图 10

等幅振荡法有一定的局限性：

① 如果工艺方面不允许被控变量做长时间的等幅振荡，这种方法就不能应用；

②如果在纯比例条件下不能出现等幅振荡，也不能用这种方法。这种方法只适用于高阶对象或具有纯滞后的对象，否则，在纯比例的作用下，系统将不会出现等幅振荡；

③如果对象时间常数较大，要使系统产生等幅振荡，临界增益 Kp可能较大，调节阀容易处于大开度变化状态，导致生产负荷大幅度变化，对生产不利。

二、衰减振荡法

衰减振荡法与ZN整定法有密切联系，其控制上做出了调整无需等幅振荡，而是直接规定了衰减比。其并非由某一单一学者提出，而是源于经典控制理论的发展，并在工业控制中逐步形成。

衰减震荡法也如临界振荡法一样需在纯比例控制的情况下调节Kp，但无需曲线出现等幅振荡，而是4/1衰减振荡。

如图11为4/1的控制曲线：

图 11

当前曲线的比例增益为Ks，第一个波峰时间减去第二个波峰时间差值为Ts。

图12为衰减振荡法的参数公式：

图 12

纯比例控制采用第一行公式，比例加积分控制采用第二行公式，比例加积分和微分控制采用第三行公式。

以PID控制为例，比例增益K=1.25Ks，积分时间Ti=9.3Ts，微分时间Td=0.1Ts。

如果4/1衰减得出的PID参数控制效果并不理想可以改用10/1衰减如图13：

图 13

其也有一定局限性：

①对于时间常数较小的系统不易测取衰减振荡周期万，干扰频繁的系统也不宜使用；

②有时4：1衰减不太好确定，只能近似。有些对象中，由于响应过程较快，从记录曲线上读出衰减比有困难。

代替的方法：观察控制器输出的变化。如果控制器输出来回摆动两次就达到稳定状态，则可以认为该过是4.1的。而波动一次的时间即T后。再根据此时控制器的Ks值就可以按照经验公式计算控制器参数。