数值分析——牛顿插值

牛顿插值

为什么要有牛顿插值

拉格朗日插值简单方便，可以一下计算出基函数，但有其本身的缺陷，回忆下拉格朗日插值基函数的形式：$$l_k(x)=\frac{(x-x_0)(x-x_1)...(x-x_{k-1})(x-x_{k+1})...(x-x_n)}{(x_k-x_0)(x_k-x_1)...(x_k-x_{k-1})(x_k-x_{k+1})...(x_k-x_n)}$$

每一个插值基函数都与所有数据点有关，这意味着如果增加一个数据点，所有基函数要重新计算。

因此我们需要一个可以逐步生成插值多项式的基函数，它应当在插值时，满足：

$$p_{n+1}(x)=p_n(x)+u_{n+1}(x)$$，其中$p_{n+1}(x)，p_n(x)$分别是$n+1$和$n$次插值多项式，这样增加一个节点时只需在当前插值多项式上加一个多余项就可以。牛顿插值就是这样一种方法。

牛顿插值基函数

现在来尝试构造一下插值基函数，虽然其形式课件里给了，但通过之前的要求未必不能自己来尝试一下找规律。

首先，如果只有一个数据点，那必然要求$p(x_0)=f(x_0)$，这可以视为系数为$f(x_0)$，基函数为${\omega }_0(x)=1$。

当增加一个数据点时，则有$p(x_0)=f(x_0)+a_1{\omega }_1(x_0)=f(x_0),p(x_1)=f(x_0)+a_1{\omega }_1(x_1)=f(x_1)$，这样可以明确的是${\omega }_1(x)$一定含有$x-x_0$项，系数$a_1$不能直接取$f(x_1)$，而是与$f(x_1)-f(x_0)$有关。如果把系数全部撇到$a_1$里先不管，那么基函数第二项为${\omega }_1(x)=(x-x_0)$，系数$a_1=\frac{f(x_1)-f(x_0)}{x_1-x_0}$。

在增加一个数据点时，同理可推出${\omega }_2(x)=(x-x_0)(x-x_1)$。且此时有：$$p(x_2)=f(x_0)+a_1{\omega }_1(x_2)+a_2{\omega }_2(x_2)=f(x_2)$$。可以解得：$$a_2=\frac{f(x_2)-f(x_0)-a_1(x_2-x_0)}{(x_2-x_0)(x_2-x_1)}=\frac{\frac{f(x_2)-f(x_1)}{x_2-x_1}-\frac{f(x_1)-f(x_0)}{x_1-x_0}}{x_2-x_0}$$

可以发现系数有明显的规律。

如果定义一阶差商：$f[x_0,x_1]=\frac{f(x_1)-f(x_0)}{x_1-x_0}$

定义n阶差商：$f[x_0,x_1,...,x_n]=\frac{f[x_1,...,x_n]-f[x_0,...,x_{n-1}]}{x_n-x_0}$

那么显然，每一项系数是：$a_k=f[x_0,x_1,...,x_k]$

每一项基函数是：${\omega }_k=(x-x_0)(x-x_1)...(x-x_{k-1})$

那么牛顿插值公式就是：$$p(x)=\sum _{k=0}^n{a}_k{\omega }_k(x)$$

等距牛顿插值

当推出牛顿插值函数通用的表达后，有一种常见情况值得单独讨论一下。

差商实际上并不好计算，但某些情况下（数据点自变量距离相等）可以用差分表示。

定义差分：$\Delta f_i=f(x_i+h)-f(x_i),...,{\Delta }^n{f}_i=\Delta ({\Delta }^{n-1}{f}_i)={\Delta }^{n-1}{f}_{i+1}-{\Delta }^{n-1}{f}_i$

那么如果$x_0,x_1,...,x_n$等距，假设这个距离是$h$，差分与差商就有一个简单对应关系：

$$f[x_0,x_1]=\frac{f(x_1)-f(x_0)}{x_1-x_0}=\frac{\Delta f_0}{h}$$

$$f[x_0,x_1,x_2]=\frac{f[x_1,x_2]-f[x_0,x_1]}{x_2-x_0}=\frac{{\Delta }^2{f}_0}{2h^2}$$

易推出：

$$f[x_0,x_1,...,x_n]=\frac{{\Delta }^m{f}_0}{m!h^m}$$

代码示例

对函数$f=cosx$进行等距插值，从$0$开始，数据点间距$0.1$。

import numpy as np
import matplotlib.pyplot as plt

# 定义数据点间距
h = 0.1
# 定义插值次数
n = 4

# 取数据点
xdata = np.linspace(0, h * (n - 1), n)
ydata = np.cos(xdata)

# 计算各阶差分
def data_different(xdata, ydata):
    num = len(xdata)
    h = xdata[1] - xdata[0]
    dif = np.zeros((num, 1))
    dif_table = ydata
    for i in range(num):
        dif[i] = dif_table[0] / (np.math.factorial(i) * h ** i)
        dif_table = np.diff(dif_table)
    return dif

# 计算插值函数
def px(factor, x, xdata, ydata):
    w = np.zeros((len(x), len(factor)))
    wk = np.ones(len(x))
    for i in range(len(factor)):
        w[:,i] = wk
        wk = wk*(x-xdata[i])
    return w@factor

plot_x = np.linspace(-2, 2, 40*n)
plot_y = px(data_different(xdata,ydata), plot_x, xdata, ydata)
p1, = plt.plot(plot_x, plot_y)
p2, = plt.plot(plot_x, np.cos(plot_x))
p3 = plt.scatter(xdata, ydata)
p3 = plt.scatter(xdata, ydata)
plt.legend([p1, p2], ["p(x)", "f(x)"])
plt.show()

当数据点数为$4$时，插值多项式的图像如下：

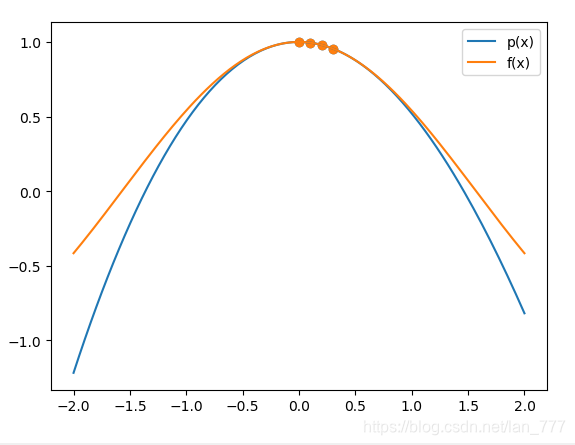
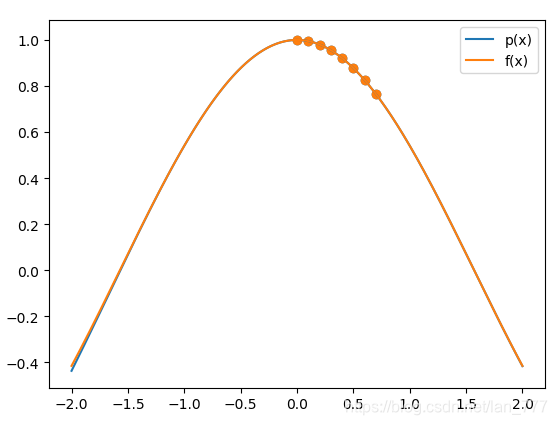
当数据点数目为$8$时，插值多项式图像如下：

现在，取$n=16$，并画出更大范围图像时，得到结果如下：

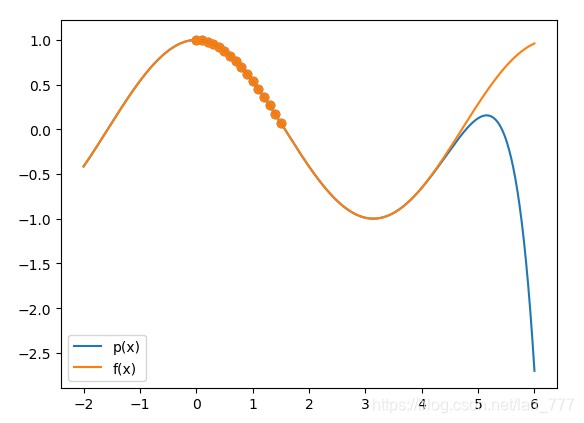
可以看出，插值并不能预知数据点范围外部的图像变化，插值插值，一般只用来计算数据点之间的函数值。

牛顿插值和拉格朗日插值比较

事实上，牛顿插值函数和拉格朗日插值函数完全一样，之前已经证明过这个定理，多项式插值函数唯一。
两者的区别仅仅是不同情形的计算方式上的优劣。