潜语义分析LSA介绍
Latent Semantic Analysis (LSA), also known as Latent Semantic Indexing (LSI) literally means analyzing documents to find the underlying meaning or concepts of those documents. If each word only meant one concept, and each concept was only described by one word, then LSA would be easy since there is a simple mapping from words to concepts.
Latent Semantic Analysis (LSA)也被叫做Latent Semantic Indexing (LSI),从字面上的意思理解就是通过分析文档去发现这些文档中潜在的意思和概念。假设每个词仅表示一个概念,并且每个概念仅仅被一个词所描述,LSA将非常简单(从词到概念存在一个简单的映射关系)

Unfortunately, this problem is difficult because English has different words that mean the same thing (synonyms), words with multiple meanings, and all sorts of ambiguities that obscure the concepts to the point where even people can have a hard time understanding.
不幸的是,这个问题并没有如此简单,因为存在不同的词表示同一个意思(同义词),一个词表示多个意思,所有这种二义性(多义性)都会混淆概念以至于有时就算是人也很难理解。

For example, the word bank when used together with mortgage, loans, and rates probably means a financial institution. However, the word bank when used together with lures, casting, and fish probably means a stream or river bank.
例如,银行这个词和抵押、贷款、利率一起出现时往往表示金融机构。但是,和鱼饵,投掷、鱼一起出现时往往表示河岸。
How Latent Semantic Analysis Works
潜语义分析工作原理
Latent Semantic Analysis arose from the problem of how to find relevant documents from search words. The fundamental difficulty arises when we compare words to find relevant documents, because what we really want to do is compare the meanings or concepts behind the words. LSA attempts to solve this problem by mapping both words and documents into a "concept" space and doing the comparison in this space.
潜语义分析(Latent Semantic Analysis)源自问题:如何从搜索query中找到相关的文档。当我们试图通过比较词来找到相关的文本时,存在着难以解决的局限性,那就是在搜索中我们实际想要去比较的不是词,而是隐藏在词之后的意义和概念。潜语义分析试图去解决这个问题,它把词和文档都映射到一个‘概念’空间并在这个空间内进行比较(注:也就是一种降维技术)。
Since authors have a wide choice of words available when they write, the concepts can be obscured due to different word choices from different authors. This essentially random choice of words introduces noise into the word-concept relationship. Latent Semantic Analysis filters out some of this noise and also attempts to find the smallest set of concepts that spans all the documents.
当文档的作者写作的时候,对于词语有着非常宽泛的选择。不同的作者对于词语的选择有着不同的偏好,这样会导致概念的混淆。这种对于词语的随机选择在 词-概念 的关系中引入了噪音。LSA滤除了这样的一些噪音,并且还能够从全部的文档中找到最小的概念集合(为什么是最小?)。
In order to make this difficult problem solvable, LSA introduces some dramatic simplifications.
1. Documents are represented as "bags of words", where the order of the words in a document is not important, only how many times each word appears in a document.
2. Concepts are represented as patterns of words that usually appear together in documents. For example "leash", "treat", and "obey" might usually appear in documents about dog training.
3. Words are assumed to have only one meaning. This is clearly not the case (banks could be river banks or financial banks) but it makes the problem tractable.
To see a small example of LSA, take a look at the next section.
为了让这个难题更好解决,LSA引入一些重要的简化:
1. 文档被表示为”一堆词(bags of words)”,因此词在文档中出现的位置并不重要,只有一个词的出现次数。
2. 概念被表示成经常出现在一起的一些词的某种模式。例如“leash”(栓狗的皮带)、“treat”、“obey”(服从)经常出现在关于训练狗的文档中。
3. 词被认为只有一个意思。这个显然会有反例(bank表示河岸或者金融机构),但是这可以使得问题变得更加容易。(这个简化会有怎样的缺陷呢?)
A Small Example
一个例子
As a small example, I searched for books using the word “investing” at Amazon.com and took the top 10 book titles that appeared. One of these titles was dropped because it had only one index word in common with the other titles. An index word is any word that:
- appears in 2 or more titles, and
- is not a very common word such as “and”, “the”, and so on (known as stop words). These words are not included because do not contribute much (if any) meaning.
In this example we have removed the following stop words: “and”, “edition”, “for”, “in”, “little”, “of”, “the”, “to”.
一个小例子,我在amazon.com上搜索”investing”(投资) 并且取top 10搜索结果的书名。其中一个被废弃了,因为它只含有一个索引词(index word)和其它标题相同。索引词可以是任何满足下列条件的词:
1. 在2个或者2个以上标题中出现 并且
2. 不是那种特别常见的词例如 “and”, ”the” 这种(停用词-stop word)。这种词没有包含进来是因为他们本身不存在什么意义。
在这个例子中,我们拿掉了如下停用词:“and”, “edition”, “for”, “in”, “little”, “of”, “the”, “to”.
Here are the 9 remaining tiles. The index words (words that appear in 2 or more titles and are not stop words) are underlined.
下面就是那9个标题,索引词(在2个或2个以上标题出现过的非停用词)被下划线标注:
1. The Neatest Little Guide to Stock Market Investing
2. Investing For Dummies, 4th Edition
3. The Little Book of Common Sense Investing: The Only Way to Guarantee Your Fair Share ofStock Market Returns
4. The Little Book of Value Investing
5. Value Investing: From Graham to Buffett and Beyond
6. Rich Dad's Guide to Investing: What the Rich Invest in, That the Poor and the Middle Class Do Not!
7. Investing in Real Estate, 5th Edition
8. Stock Investing For Dummies
9. Rich Dad's Advisors: The ABC's of Real Estate Investing: The Secrets of Finding Hidden Profits Most Investors Miss
Once Latent Semantic Analysis has been run on this example, we can plot the index words and titles on an XY graph and identify clusters of titles. The 9 titles are plotted with blue circles and the 11 index words are plotted with red squares. Not only can we spot clusters of titles, but since index words can be plotted along with titles, we can label the clusters. For example, the blue cluster, containing titles T7 and T9, is about real estate. The green cluster, with titles T2, T4, T5, and T8, is about value investing, and finally the red cluster, with titles T1 and T3, is about the stock market. The T6 title is an outlier, off on its own.
在这个例子里面应用了LSA,我们可以在XY轴的图中画出词和标题的位置(只有2维),并且识别出标题的聚类。蓝色圆圈表示9个标题,红色方块表示11个索引词。我们不但能够画出标题的聚类,并且由于索引词可以被画在标题一起,我们还可以给这些聚类打标签。例如,蓝色的聚类,包含了T7和T9,是关于real estate(房地产)的,绿色的聚类,包含了标题T2,T4,T5和T8,是讲value investing(价值投资)的,最后是红色的聚类,包含了标题T1和T3,是讲stock market(股票市场)的。标题T6是孤立点(outlier)

In the next few sections, we'll go through all steps needed to run Latent Semantic Analysis on this example.
在下面的部分,我们会通过这个例子介绍LSA的整个流程。
Part 1 - Creating the Count Matrix
第一部分 - 创建计数矩阵
The first step in Latent Semantic Analysis is to create theword by title (or document) matrix. In this matrix, each index word is a rowand each title is a column. Each cell contains the number of times that wordoccurs in that title. For example, the word "book" appears one timein title T3 and one time in title T4, whereas "investing" appears onetime in every title. In general, the matrices built during LSA tend to be verylarge, but also very sparse (most cells contain 0). That is because each titleor document usually contains only a small number of all the possible words.This sparseness can be taken advantage of in both memory and time by moresophisticated LSA implementations.
LSA的第一步是要去创建词到标题(文档)的矩阵。在这个矩阵里,每一个索引词占据了一行,每一个标题占据一列。每一个单元(cell)包含了这个词出现在那个标题中的次数。例如,词”book”出现在T3中一次,出现在T4中一次,而” investing”在所有标题中都出现了一次。一般来说,在LSA中的矩阵会非常大而且会非常稀疏(大部分的单元都是0)。这是因为每个标题或者文档一般只包含所有词汇的一小部分。更复杂的LSA算法会利用这种稀疏性去改善空间和时间复杂度。
In the following matrix, we have left out the 0's to reduceclutter.
| Index Words | Titles | ||||||||
| T1 | T2 | T3 | T4 | T5 | T6 | T7 | T8 | T9 | |
| book | 1 | 1 | |||||||
| dads | 1 | 1 | |||||||
| dummies | 1 | 1 | |||||||
| estate | 1 | 1 | |||||||
| guide | 1 | 1 | |||||||
| investing | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| market | 1 | 1 | |||||||
| real | 1 | 1 | |||||||
| rich | 2 | 1 | |||||||
| stock | 1 | 1 | 1 | ||||||
| value | 1 | 1 | |||||||
Python - Getting Started
Download the python code here.
Throughout this article, we'll givePython code that implements all the steps necessary for doing Latent SemanticAnalysis. We'll go through the code section by section and explain everything.The Python code used in this article can be downloaded here and then run in Python. You need to havealready installed the Python NumPy and SciPy libraries.
在这篇文章中,我们用python代码去实现LSA的所有步骤。我们将介绍所有的代码。Python代码可以在这里被下到(见上)。需要安装NumPy 和 SciPy这两个库。
Python - Import Functions
First we need to import a few functions from Python librariesto handle some of the math we need to do. NumPy is the Python numericallibrary, and we'll import zeros, a function that creates a matrix of zeros thatwe use when building our words by titles matrix. From the linear algebra partof the scientific package (scipy.linalg) we import the svd function thatactually does the singular value decomposition, which is the heart of LSA.
NumPy是python的数值计算类,用到了zeros(初始化矩阵),scipy.linalg这个线性代数的库中,我们引入了svd函数也就是做奇异值分解,LSA的核心。
from numpy import zeros
from scipy.linalg import svdPython - Define Data
Next, we define the data that we are using. Titles holds the9 book titles that we have gathered, stopwords holds the 8 common words that weare going to ignore when we count the words in each title, and ignorechars hasall the punctuation characters that we will remove from words. We use Python'striple quoted strings, so there are actually only 4 punctuation symbols we areremoving: comma (,), colon (:), apostrophe ('), and exclamation point (!).
Stopwords 是停用词 ignorechars是无用的标点
titles =
[
"The Neatest Little Guide to Stock Market Investing",
"Investing For Dummies, 4th Edition",
"The Little Book of Common Sense Investing: The Only Way to Guarantee Your Fair Share of Stock Market Returns",
"The Little Book of Value Investing",
"Value Investing: From Graham to Buffett and Beyond",
"Rich Dad's Guide to Investing: What the Rich Invest in, That the Poor and the Middle Class Do Not!",
"Investing in Real Estate, 5th Edition",
"Stock Investing For Dummies",
"Rich Dad's Advisors: The ABC's of Real Estate Investing: The Secrets of Finding Hidden Profits Most Investors Miss"
]
stopwords = ['and','edition','for','in','little','of','the','to']
ignorechars = ''',:'!'''
Python - Define LSA Class
The LSA class has methods for initialization, parsingdocuments, building the matrix of word counts, and calculating. The firstmethod is the __init__ method, which is called whenever an instance of the LSAclass is created. It stores the stopwords and ignorechars so they can be usedlater, and then initializes the word dictionary and the document countvariables.
这里定义了一个LSA的类,包括其初始化过程wdict是词典,dcount用来记录文档号。
class LSA(object):
def __init__(self, stopwords, ignorechars):
self.stopwords = stopwords
self.ignorechars = ignorechars
self.wdict = {}
self.dcount = 0
Python - Parse Documents
The parse method takes a document, splits it into words, removesthe ignored characters and turns everything into lowercase so the words can becompared to the stop words. If the word is a stop word, it is ignored and wemove on to the next word. If it is not a stop word, we put the word in thedictionary, and also append the current document number to keep track of whichdocuments the word appears in.
The documents that each word appears in are kept in a listassociated with that word in the dictionary. For example, since the word bookappears in titles 3 and 4, we would have self.wdict['book'] = [3, 4] after alltitles are parsed.
After processing all words from the current document, weincrease the document count in preparation for the next document to be parsed.
这个函数就是把文档拆成词并滤除停用词和标点,剩下的词会把其出现的文档号填入到wdict中去,例如,词book出现在标题3和4中,则我们有self.wdict['book'] = [3, 4]。相当于建了一下倒排。
def parse(self, doc):
words = doc.split(); for w in words:
w = w.lower().translate(None, self.ignorechars)
if w in self.stopwords:
continue
elif w in self.wdict:
self.wdict[w].append(self.dcount)
else:
self.wdict[w] = [self.dcount]
self.dcount += 1Python - Build the Count Matrix
Once all documents are parsed, all the words (dictionarykeys) that are in more than 1 document are extracted and sorted, and a matrix isbuilt with the number of rows equal to the number of words (keys), and thenumber of columns equal to the document count. Finally, for each word (key) anddocument pair the corresponding matrix cell is incremented.
所有的文档被解析之后,所有出现的词(也就是词典的keys)被取出并且排序。建立一个矩阵,其行数是词的个数,列数是文档个数。最后,所有的词和文档对所对应的矩阵单元的值被统计出来。
def build(self):
self.keys = [k for k in self.wdict.keys() if len(self.wdict[k]) > 1]
self.keys.sort()
self.A = zeros([len(self.keys), self.dcount])
for i, k in enumerate(self.keys):
for d in self.wdict[k]:
self.A[i,d] += 1
Python - Print the Count Matrix
The printA() method is very simple, it just prints out thematrix that we have built so it can be checked.
把矩阵打印出来
def printA(self):
print self.APython - Test the LSA Class
After defining the LSA class, it's time to try it out on our9 book titles. First we create an instance of LSA, called mylsa, and pass itthe stopwords and ignorechars that we defined. During creation, the __init__method is called which stores the stopwords and ignorechars and initializes theword dictionary and document count.
Next, we call the parse method on each title. This methodextracts the words in each title, strips out punctuation characters, convertseach word to lower case, throws out stop words, and stores remaining words in adictionary along with what title number they came from.
Finally we call the build() method to create the matrix ofword by title counts. This extracts all the words we have seen so far, throwsout words that occur in less than 2 titles, sorts them, builds a zero matrix ofthe right size, and then increments the proper cell whenever a word appears ina title.
mylsa = LSA(stopwords, ignorechars)
for t in titles:
mylsa.parse(t)
mylsa.build()
mylsa.printA()Here is the raw output produced by printA(). As you can see,it's the same as the matrix that we showed earlier.
在刚才的测试数据中验证程序逻辑,并查看最终生成的矩阵:
[[ 0. 0. 1. 1. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 1. 0. 0. 1.]
[ 0. 1. 0. 0. 0. 0. 0. 1. 0.]
[ 0. 0. 0. 0. 0. 0. 1. 0. 1.]
[ 1. 0. 0. 0. 0. 1. 0. 0. 0.]
[ 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[ 1. 0. 1. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 1. 0. 1.]
[ 0. 0. 0. 0. 0. 2. 0. 0. 1.]
[ 1. 0. 1. 0. 0. 0. 0. 1. 0.]
[ 0. 0. 0. 1. 1. 0. 0. 0. 0.]]Part 2 - Modify the Counts with TFIDF
计算TFIDF替代简单计数
In sophisticated Latent Semantic Analysis systems, the raw matrix countsare usually modified so that rare words are weighted more heavily than commonwords. For example, a word that occurs in only 5% of the documents shouldprobably be weighted more heavily than a word that occurs in 90% of thedocuments. The most popular weighting is TFIDF (Term Frequency - InverseDocument Frequency). Under this method, the count in each cell is replaced bythe following formula.
在复杂的LSA系统中,为了重要的词占据更重的权重,原始矩阵中的计数往往会被修改。例如,一个词仅在5%的文档中应该比那些出现在90%文档中的词占据更重的权重。最常用的权重计算方法就是TFIDF(词频-逆文档频率)。基于这种方法,我们把每个单元的数值进行修改:
TFIDFi,j = ( Ni,j / N*,j ) * log( D / Di) where
- Ni,j = the number of times word i appears in document j (the original cell count).
- N*,j = the number of total words in document j (just add the counts in column j).
- D = the number of documents (the number of columns).
- Di = the number of documents in which word i appears (the number of non-zero columns in row i).
Nij = 某个词i出现在文档j的次数(矩阵单元中的原始值)
N*j= 在文档j中所有词的个数(就是列j上所有数值的和)
D = 文档个数(也就是矩阵的列数)
Di= 包含词i的文档个数(也就是矩阵第i行非0列的个数)
In this formula, words that concentrate in certain documents areemphasized (by the Ni,j / N*,jratio) and words that onlyappear in a few documents are also emphasized (by the log( D / Di )term).
Since we have such a small example, we will skip this step and move on theheart of LSA, doing the singular value decomposition of our matrix of counts.However, if we did want to add TFIDF to our LSA class we could add the followingtwo lines at the beginning of our python file to import the log, asarray, andsum functions.
在这个公式里,在某个文档中密集出现的词被加强(通过Nij/N*j),那些仅在少数文档中出现的词也被加强(通过log(D/Di))
因为我们的例子过小,这里将跳过这一个步骤直接进入LSA的核心部分,对我们的计数矩阵做SVD。然而,如果我们需要增加TFIDF到这个LSA类中,我们需要加入以下两行代码。
from math importlog
from numpy import asarray, sumThen we would add the following TFIDF method to our LSA class. WordsPerDoc(N*,j) just holds the sum of each column, which is the total numberof index words in each document. DocsPerWord (Di) uses asarray tocreate an array of what would be True and False values, depending on whetherthe cell value is greater than 0 or not, but the 'i' argument turns it into 1'sand 0's instead. Then each row is summed up which tells us how many documentseach word appears in. Finally, we just step through each cell and apply theformula. We do have to change cols (which is the number of documents) into afloat to prevent integer division.
接下来需要增加下面这个TFIDF方法到我们的LSA类中。WordsPerDoc 就是矩阵每列的和,也就是每篇文档的词语总数。DocsPerWord 利用asarray方法创建一个0、1数组(也就是大于0的数值会被归一到1),然后每一行会被加起来,从而计算出每个词出现在了多少文档中。最后,我们对每一个矩阵单元计算TFIDF公式
def TFIDF(self):
WordsPerDoc = sum(self.A, axis=0)
DocsPerWord = sum(asarray(self.A > 0,'i'), axis=1)
rows, cols = self.A.shape
for i in range(rows):
for j in range(cols):
self.A[i,j] = (self.A[i,j] /WordsPerDoc[j]) * log(float(cols) / DocsPerWord[i])Part 3 - Usingthe Singular Value Decomposition
使用奇异值分解
Oncewe have built our (words by titles) matrix, we call upon a powerful but littleknown technique called Singular Value Decomposition or SVD to analyze thematrix for us. The"SingularValue Decomposition Tutorial" is a gentle introduction for readers that want to learn moreabout this powerful and useful algorithm.
一旦我们建立了词到标题的矩阵,我们就能够利用一个非常强大的工具“奇异值分解”去为我们分析这个矩阵。“"Singular Value DecompositionTutorial”是其的一个介绍。
Thereason SVD is useful, is that it finds a reduced dimensional representation ofour matrix that emphasizes the strongest relationships and throws away thenoise. In other words, it makes the best possible reconstruction of the matrixwith the least possible information. To do this, it throws out noise, whichdoes not help, and emphasizes strong patterns and trends, which do help. Thetrick in using SVD is in figuring out how many dimensions or"concepts" to use when approximating the matrix. Too few dimensionsand important patterns are left out, too many and noise caused by random wordchoices will creep back in.
SVD非常有用的原因是,它能够找到我们矩阵的一个降维表示,他强化了其中较强的关系并且扔掉了噪音(这个算法也常被用来做图像压缩)。换句话说,它可以用尽可能少的信息尽量完善的去重建整个矩阵。为了做到这点,它会扔掉无用的噪音,强化本身较强的模式和趋势。利用SVD的技巧就是去找到用多少维度(概念)去估计这个矩阵。太少的维度会导致重要的模式被扔掉,反之维度太多会引入一些噪音。
TheSVD algorithm is a little involved, but fortunately Python has a libraryfunction that makes it simple to use. By adding the one line method below toour LSA class, we can factor our matrix into 3 other matrices. The U matrixgives us the coordinates of each word on our “concept” space, the Vt matrixgives us the coordinates of each document in our “concept” space, and the Smatrix of singular values gives us a clue as to how many dimensions or“concepts” we need to include.
这里SVD算法介绍的很少,但是幸运的是python有一个简单好用的类库(scipy不是太好装)。如下述代码所示,我们在LSA类中增加了一行代码,这行代码把矩阵分解为另外三个矩阵。矩阵U告诉我们每个词在我们的“概念”空间中的坐标,矩阵Vt 告诉我们每个文档在我们的“概念”空间中的坐标,奇异值矩阵S告诉我们如何选择维度数量的线索(需要去研究下为什么)。
def calc(self):
self.U, self.S, self.Vt = svd(self.A)Inorder to choose the right number of dimensions to use, we can make a histogramof the square of the singular values. This graphs the importance each singularvalue contributes to approximating our matrix. Here is the histogram in ourexample.
为了去选择一个合适的维度数量,我们可以做一个奇异值平方的直方图。它描绘了每个奇异值对于估算矩阵的重要度。下图是我们这个例子的直方图。(每个奇异值的平方代表了重要程度,下图应该是归一化后的结果)

Forlarge collections of documents, the number of dimensions used is in the 100 to500 range. In our little example, since we want to graph it, we’ll use 3dimensions, throw out the first dimension, and graph the second and thirddimensions.
对于大规模的文档,维度选择在100到500这个范围。在我们的例子中,因为我们打算用图表来展示最后的结果,我们使用3个维度,扔掉第一个维度,用第二和第三个维度来画图(为什么扔掉第一个维度?)。
Thereason we throw out the first dimension is interesting. For documents, thefirst dimension correlates with the length of the document. For words, it correlateswith the number of times that word has been used in all documents. If we hadcentered our matrix, by subtracting the average column value from each column,then we would use the first dimension. As an analogy, consider golf scores. Wedon’t want to know the actual score, we want to know the score aftersubtracting it from par. That tells us whether the player made a birdie, bogie,etc.
我们扔掉维度1的原因非常有意思。对于文档来说,第一个维度和文档长度相关。对于词来说,它和这个词在所有文档中出现的次数有关(为什么?)。如果我们已经对齐了矩阵(centering matrix),通过每列减去每列的平均值,那么我们将会使用维度1(为什么?)。类似的,像高尔夫分数。我们不会想要知道实际的分数,我们想要知道减去标准分之后的分数。这个分数告诉我们这个选手打到小鸟球、老鹰球(猜)等等。
Thereason we don't center the matrix when using LSA, is that we would turn asparse matrix into a dense matrix and dramatically increase the memory andcomputation requirements. It's more efficient to not center the matrix and thenthrow out the first dimension.
我们没有对齐矩阵的原因是,对齐后稀疏矩阵会变成稠密矩阵,而这将大大增加内存和计算量。更有效的方法是并不对齐矩阵并且扔掉维度1.
Hereis the complete 3 dimensional Singular Value Decomposition of our matrix. Eachword has 3 numbers associated with it, one for each dimension. The first numbertends to correspond to the number of times that word appears in all titles andis not as informative as the second and third dimensions, as we discussed.Similarly, each title also has 3 numbers associated with it, one for eachdimension. Once again, the first dimension is not very interesting because ittends to correspond to the number of words in the title.
下面是我们矩阵经过SVD之后3个维度的完整结果。每个词都有三个数字与其关联,一个代表了一维。上面讨论过,第一个数字趋向于和该词出现的所有次数有关,并且不如第二维和第三维更有信息量。类似的,每个标题都有三个数字与其关联,一个代表一维。同样的,我们对第一维不感兴趣,因为它趋向于和每个标题词的数量有关系。
| * |
| * |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Part 4 - Clustering by Color
用颜色聚类
We can also turnthe numbers into colors. For instance, here is a color display that correspondsto the first 3 dimensions of the Titles matrix that we showed above. Itcontains exactly the same information, except that blue shows negative numbers,red shows positive numbers, and numbers close to 0 are white. For example,Title 9, which is strongly positive in all 3 dimensions, is also strongly redin all 3 dimensions.
我们可以把数字转换为颜色。例如,下图表示了标题矩阵3个维度的颜色分布。除了蓝色表示负值,红色表示正值,它包含了和矩阵同样的信息。例如,标题9在所有三个维度上正数值都较大,那么它在3个维度上都会很红。
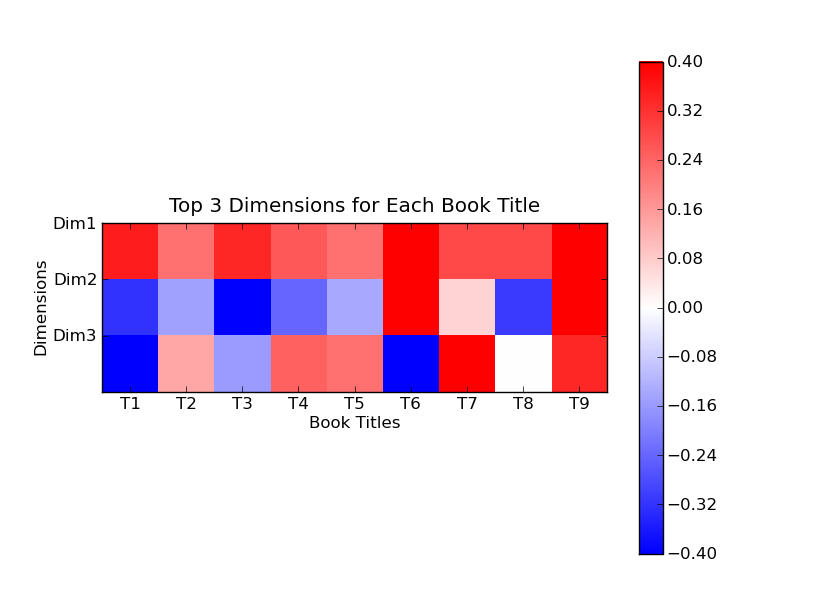
We can use thesecolors to cluster the titles. We ignore the first dimension for clusteringbecause all titles are red. In the second dimension, we have the followingresult.
我们能够利用这些颜色来把标题聚类。我们在聚类中忽略第一维度,因为所有的都是红色。在第二维度,我们有如下结果:
| Dim2 | Titles |
| red | 6-7, 9 |
| blue | 1-5, 8 |
Using the thirddimension, we can split each of these groups again the same way. For example,looking at the third dimension, title 6 is blue, but title 7 and title 9 arestill red. Doing this for both groups, we end up with these 4 groups.
在加上第三维度,我们可以继续划分。例如,在维度3上,标题6是蓝色,但是标题7和标题9依然是红色。最终我们得到如下几个分组:
| Dim2 | Dim3 | Titles |
| red | red | 7, 9 |
| red | blue | 6 |
| blue | red | 2, 4-5, 8 |
| blue | blue | 1, 3 |
It’s interestingto compare this table with what we get when we graph the results in the nextsection.
Part 5 - Clustering by Value
按值聚类
Leaving out thefirst dimension, as we discussed, let's graph the second and third dimensionsusing a XY graph. We'll put the second dimension on the X axis and the thirddimension on the Y axis and graph each word and title. It's interesting tocompare the XY graph with the table we just created that clusters thedocuments.
去掉维度1,让我们用xy轴坐标图来画出第二维和第三维。第二维作为X、第三维作为Y,并且把每个词和标题都画上去。比较下这个图和刚才聚类的表格会非常有意思。
In the graphbelow, words are represented by red squares and titles are represented by bluecircles. For example the word "book" has dimension values (0.15,-0.27, 0.04). We ignore the first dimension value 0.15 and graph"book" to position (x = -0.27, y = 0.04) as can be seen in the graph.Titles are similarly graphed.
在下图中,词表示为红色方形,标题表示为蓝色圆圈。例如,词“book”有坐标值(0.15, -0.27,0.04)。这里我们忽略第一维度0.15 把点画在(x = -0.27, y =0.04)。标题也是一样。
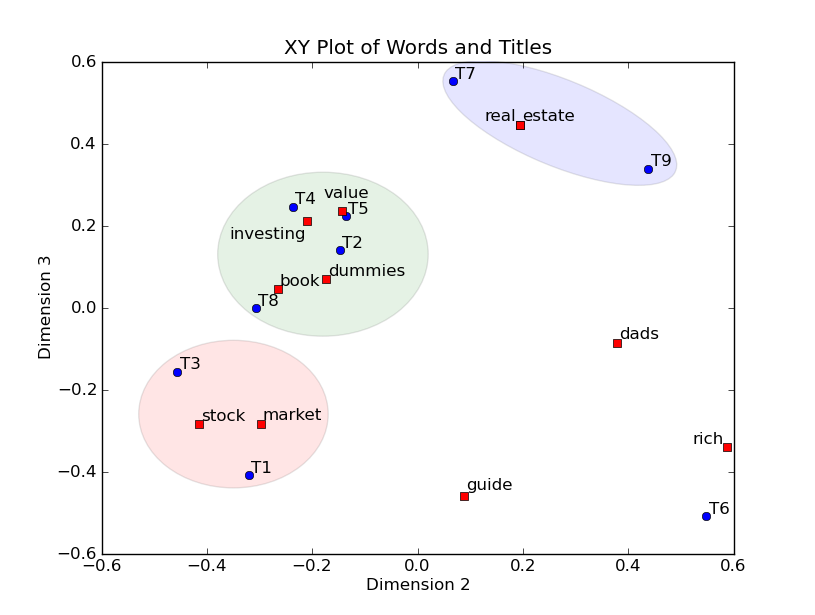
One advantage ofthis technique is that both words and titles are placed on the same graph. Notonly can we identify clusters of titles, but we can also label the clusters bylooking at what words are also in the cluster. For example, the lower leftcluster has titles 1 and 3 which are both about stock market investing. Thewords "stock" and "market" are conveniently located in thecluster, making it easy to see what the cluster is about. Another example isthe middle cluster which has titles 2, 4, 5, and, to a somewhat lesser extent,title 8. Titles 2, 4, and 5 are close to the words "value" and"investing" which summarizes those titles quite well.
这个技术的一个有点是词和标题都在一张图上。不仅我们可以区分标题的聚类,而且我们可以把聚类中的词给这个聚类打上标签。例如左下的聚类中有标题1和标题3都是关于股票市场投资(stock market investing)的。Stock和market可以方便的定位在这个聚类中,让描述这个聚类变得容易。其它也类似。
Advantages, Disadvantages, and Applications of LSA
LSA的优势、劣势以及应用
Latent SemanticAnalysis has many nice properties that make it widely applicable to manyproblems.
1. First, the documents and words end up being mapped to thesame concept space. In this space we can cluster documents, cluster words, andmost importantly, see how these clusters coincide so we can retrieve documentsbased on words and vice versa.
2. Second, the concept space has vastly fewer dimensionscompared to the original matrix. Not only that, but these dimensions have beenchosen specifically because they contain the most information and least noise.This makes the new concept space ideal for running further algorithms such astesting different clustering algorithms.
3. Last, LSA is an inherently global algorithm that looks attrends and patterns from all documents and all words so it can find things thatmay not be apparent to a more locally based algorithm. It can also be usefullycombined with a more local algorithm such as nearest neighbors to become moreuseful than either algorithm by itself.
LSA有着许多优良的品质使得其应用广泛:
1. 第一,文档和词被映射到了同一个“概念空间”。在这个空间中,我们可以把聚类文档,聚类词,最重要的是可以知道不同类型的聚类如何联系在一起的,这样我们可以通过词来寻找文档,反之亦然。
2. 第二,概念空间比较原始矩阵来说维度大大减少。不仅如此,这种维度数量是刻意为之的,因为他们包含了大部分的信息和最少的噪音。这使得新产生的概念空间对于运行之后的算法非常理想,例如尝试不同的聚类算法。
3. 最后LSA天生是全局算法,它从所有的文档和所有的词中找到一些东西,而这是一些局部算法不能完成的。它也能和一些更局部的算法(最近邻算法nearest neighbors)所结合发挥更大的作用。
There are a fewlimitations that must be considered when deciding whether to use LSA. Some ofthese are:
1. LSA assumes a Gaussian distribution and Frobenius normwhich may not fit all problems. For example, words in documents seem to followa Poisson distribution rather than a Gaussian distribution.
2. LSA cannot handle polysemy (words with multiple meanings)effectively. It assumes that the same word means the same concept which causesproblems for words like bank that have multiple meanings depending on whichcontexts they appear in.
3. LSA depends heavily on SVD which is computationallyintensive and hard to update as new documents appear. However recent work hasled to a new efficient algorithm which can update SVD based on new documents ina theoretically exact sense.
当选择使用LSA时也有一些限制需要被考量。其中的一些是:
1. LSA假设Gaussiandistribution and Frobenius norm,这些假设不一定适合所有问题。例如,文章中的词符合Poissondistribution而不是Gaussian distribution。
2. LSA不能够有效解决多义性(一个词有多个意思)。它假设同样的词有同样的概念,这就解决不了例如bank这种词需要根据语境才能确定其具体含义的。
3. LSA严重依赖于SVD,而SVD计算复杂度非常高并且对于新出现的文档很难去做更新。然而,近期出现了一种可以更新SVD的非常有效的算法。
In spite ofthese limitations, LSA is widely used for finding and organizing searchresults, grouping documents into clusters, spam filtering, speech recognition,patent searches, automated essay evaluation, etc.
不考虑这些限制,LSA被广泛应用在发现和组织搜索结果,把文章聚类,过滤作弊,语音识别,专利搜索,自动文章评价等应用之上。
As an example,iMetaSearch uses LSA to map search results and words to a “concept” space.Users can then find which results are closest to which words and vice versa.The LSA results are also used to cluster search results together so that yousave time when looking for related results.
例如,iMetaSearch利用LSA去把搜索结果和词映射到“概念”空间。用户可以知道那些结果和那些词更加接近,反之亦然。LSA的结果也被用在把搜索结果聚在一起,这样你可以节约寻找相关结果的时间。
转自---------------http://blog.csdn.net/yihucha166/article/category/419357
























 1335
1335

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








