机器学习 之 LBP特征

综述：：
LBP特征：Local Binary Pattern，局部二值模式特征，是一种用来描述图像局部纹理特征的算子。LBP特征算子计算简单、效果较好，数据量小，因此LBP特征在计算机视觉的许多领域都得到了广泛的应用，LBP特征比较多用于目标检测中。LBP计算出的特征具有灰度不变性和旋转不变性等显著优点，例如对光照不敏感。

LBP的基本算子

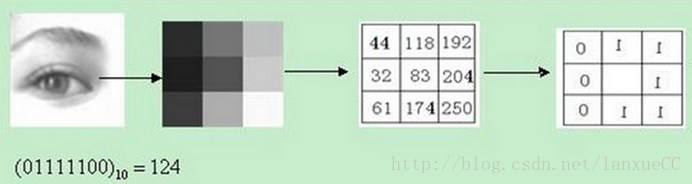
原始的LBP算子定义为在3*3的窗口内，以窗口中心像素为阈值，将相邻的8个像素的灰度值与其进行比较，若周围像素值大于中心像素值，则该像素 点的位置被标记为1，否则为0。这样，3*3邻域内的8个点经过比较可产生8个0或1，将这8个0或1作为二进制数按照一定的次序排列形成一个二进制数字，这个二进制数字就是中心像素的LBP值。LBP值共有 种可能，因此LBP值有256种。像素之间的比较反映的是一种像素之间的差异关系，能够很好反映图像局部纹理这种特征。

LBP特征的改进

http://blog.csdn.net/pi9nc/article/details/26678691
http://blog.csdn.net/quincuntial/article/details/50541815
http://www.open-open.com/lib/view/open1440832074794.html
这三篇博客对LBP特征的改进版本均有很好的描述，我在这里做个总结：

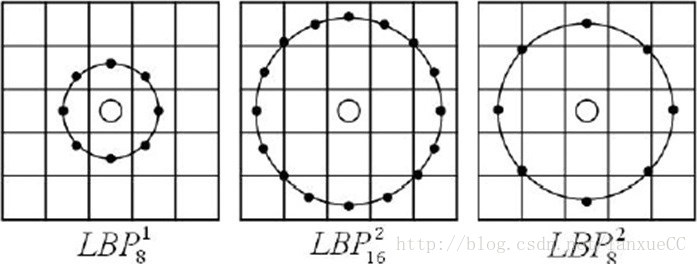
圆形LBP算子：

所谓圆形LBP算子：如果要计算某个像素的点LBP特征，以这个像素点为中心，以一个任意大小半径R画一个圆，将落在圆内的像素与中心点像素比较得到LBP算子。如下图：

这样做的好处是：它能够适应一定程序上纹理的尺度变化，并达到灰度和旋 转不变性的要求。

LBP旋转不变模式

首先讲下为什么LBP特征会有旋转可变这个情况，就是以上面3x3区域的像素值为例：

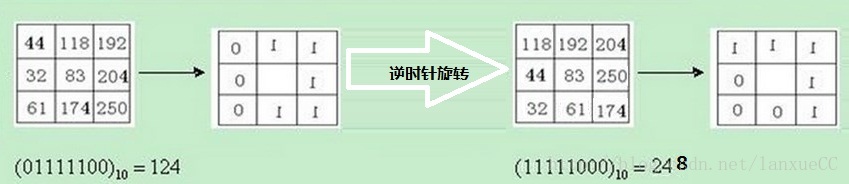
逆时针旋转一格后得到的LBP值与原始不同。
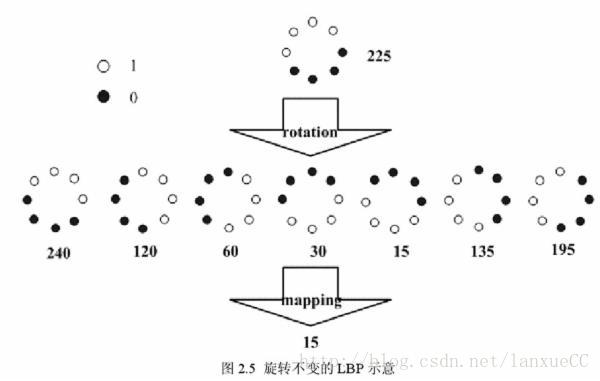
那么旋转不变模式是什么呢，就是旋转圆形邻域一周得到一系列初始定义的 LBP值，取其最小值作为该邻域的 LBP 值，这样无论怎样旋转，该点LBP值始终不变。如下图所示：

LBP等价模式

具体可见上面三个博客里的介绍，总的来说：
原来是LBP的每个位都作为该特征的决定项，例如01100100与01101100被认为是两个不同的特征值，采用LBP的等价模式后，只认为0到1的跳变与1到0的跳变为一个特征决定项，那么这样说的话，01100100中0～1有2个，1～0有2个，而01101100中0～1有2个，1～0也是有2个，我们认为它是同一个特征，这样LBP特征的种类就大减少了。

opencv中LBP特征实现

opencv中LBP特征的实现原理：将一个图像窗