//红黑二叉查找树
//红黑二叉查找树是一种平衡二叉树,是基于2-3查找树的基础上演变的
//这里不对2-3查找树的算法进行描述,感兴趣的朋友可以自行了解一下
//2-3查找树的实现原理.
//
//在2-3查找树算法中,难点就是3-Node类型(含有2个key,3个子节点的节点类型)
//的节点数据结构处理,那么在红黑二叉查找树中这种3-Node类型节点演变为如
//下表示方式.非常巧妙的在原普通二叉数结点数据结构中增加了一个颜色的成
//员变量,就使得红黑二叉查找树可以替换为2-3查找树.当一个节点的左子节点
//的颜色为红色时,该节点即为2-3查找树中的3-Node类型节点,此时可以将红
//色的子节点理解为和父节点是平行的,一体的,比如当前示例中将Node1与
//Node2合并成一个节点,该节点相当于2-3查找树中的3-Node类型节点,即含有
//2个key,3个子节点。
//
// ** 相当于2-3查找树中的3-Node类型节点:
// Node1(Black)
// --------------
// / \
// Node2(Red) NULL(Black)
// -----------
// / \
// NULL(Black) NULL(Black)
//
// ** 相当于2-3查找树中的2-Node类型节点:
// Node1(Black)
// --------------
// / \
// Node2(Black) NULL(Black)
// -----------
// / \
// NULL(Black) NULL(Black)
//
//红黑二叉查找树的定义如下:
//1 根节点必须为黑色
//2 红链接均为左链接
//3 没有任何一个结点同时和两条红链接相连
//4 该树是完美黑色平衡的,即任意空链接到根结点的路径上的黑链接数量
// 相同。
//备注: 空节点的颜色为黑色。
private const bool RED = true;
private const bool BLACK = false;
private Node root;
class Node
{
public Node Left { get; set; }
public Node Right { get; set; }
public TKey Key { get; set; }
public TValue Value { get; set; }
public int Number { get; set; }
public bool Color { get; set; }
public Node(TKey key, TValue value,int number, bool color)
{
this.Key = key;
this.Value = value;
this.Number = number;
this.Color = color;
}
}
private bool IsRed(Node node)
{
if (node == null) return false;
return node.Color == RED;
}
//树的左旋:
//1 首先把该节点的右子节点进行提升
//2 之后把该节点进行下降(由于右子节点提升,该节点下降,所以此刻该节点的等级
// 仅仅和新位置的右子点的子节点平行,即当前右子节点已经可以做为被旋转节点
// 的父节点了)
//3 将该节点的右链接指向原右子节点的左树
//4 将原右子节点的左链接指向该节点
// (3、4步之所以这样操作,主要是为了满足二叉树的特性,每个节点最多有两个子
// 节点,同时左子节点一定小于该节点,右子节点一定大于该节点。)
//5 可以看到当前仅被旋转节点和该节点的右子节点做了变化,所以仅对这两个节点
// 的相关信息进行更新。
//
//示例:对5节点进行左旋
//
// 旋转前
// 5
// / \
// 3 7
// / \ / \
// 2 4 6 8
//
// 旋转后
// 7
// / \
// 5 8
// / \
// 3 6
// / \
// 2 4
//
//左旋转
private Node RotateLeft(Node h)
{
Node x = h.Right;
//将x的左节点复制给h右节点
h.Right = x.Left;
//将h复制给x右节点
x.Left = h;
x.Color = h.Color;
h.Color = RED;
return x;
}
//树的右旋:
//同左旋原理相同,这里仅给出示例
//
//示例:对5节点进行右旋
//
// 旋转前
// 5
// / \
// 3 7
// / \ / \
// 2 4 6 8
//
// 旋转后
// 3
// / \
// 2 5
// / \
// 4 7
// / \
// 6 8
//
//右旋转
private Node RotateRight(Node h)
{
Node x = h.Left;
h.Left = x.Right;
x.Right = h;
x.Color = h.Color;
h.Color = RED;
return x;
}
void flipColors(Node h){
h.color = RED;
h.left.color = BLACK;
h.right.color = BLACK;
}
//红黑二叉查找树的插入
//这里同2-3查找树算法类似,主要考虑5种情况:
//1 插入到2-Node类型节点的左侧
//2 插入到2-Node类型节点的右侧
//3 插入到3-Node类型节点的左侧
//4 插入到3-Node类型节点的中侧
//5 插入到3-Node类型节点的右侧
//
// * 插入到2-Node类型节点的左侧
// 如下示例所示,将2插入到4节点的左侧,新建立的节点都是红色,此时
// 满足红黑树的特性,所以后继不需要在做其它处理。
//
// 插入前:
// 4(B)
// / \
// NULL 6(B)
//
// 插入后:
// 4(B)
// / \
// 2(R) 6(B)
//
// * 插入到2-Node类型节点的右侧
// 如下示例所示,将6插入到4节点的右侧,新建立的节点是红色,此时
// 违背了红黑树的特性,不能出现红色的右链接,为了恢复红黑树的特性,
// 这里需要再将4节点进行左旋转,可以参见树左旋的介绍,这样红黑
// 树的特性又满足了。
//
// 插入前:
// 4(B)
// / \
// 5(B) NULL
//
// 插入后:
// 4(B)
// / \
// 5(B) 6(R)
//
// * 插入到3-Node类型节点的右侧
// 先介绍这种情况,因为这种情况在3-Node类型节点的几种插入算法中最简单。
// 如下示例所示,将8插入到7节点的右侧,新建立的节点为红色,由于这里是
// 将新节点插入到3-Node类型节点中,所以不能依照2-Node类型算法中的插入
// 右侧进行分析,3-Node类型节点的插入有自己单独的算法,在插入3-Node类
// 型节点右侧的情况下,将7的左、右两个子节点5和8的颜色全部变成黑色,之
// 后7节点自身的颜色变成红色,这时候关键就看7这个节点,如果7节点也是一棵
// 子树,则由于7节点颜色发生了变化,所以需要检测7节点上面的父节点情况,
// 一般情况下父节点会有3种情况
// a 如果父节点不存在,则7就是最根节点,则根节点7为了满足红黑树的特性,
// 必须变成黑色
// b 如果父节点为2-Node类型节点,则按照上面2-Node的两种方法进行调用父
// 节点也当前子树根节点的关系即可
// c 如果父节点为3-Node类型节点,则同当前3-Node类型节点的方法相同,调
// 整父节点与当前子树根节点的关系,采用这种循环处理父节点的方式,
// 直到上升调整到父节点为空或为2-Node类型则停止。
// (此时的算法已经十分类似向2-3查找树算法中,向3-Node类型节点插入相似)
//
// 插入前:
// 7(B)
// / \
// 5(R) NULL
// / \
// 3(B) 6(B)
//
// 插入后:
// 7(B)
// / \
// 5(R) 8(R)
// / \
// 3(B) 6(B)
//
// * 插入到3-Node类型节点的左侧
// 如示例所示,将节点3插入到3-Node类型节点左侧,新建的节点是红色,
// 插入后,出现7的左节点为红色,同时左节点的左节点也是红色,此时不
// 能满足红黑树的特性,之后将节点7进行右旋,仔细查看右旋后的情况,
// 和之前"插入到3-Node类型节点的右侧"后的情况竟然相同了,此时参数
// 上述方法,将两个子节点变成黑色,当前子树的根节点变成红色即可。
//
// 插入前:
// 7(B)
// / \
// 5(R) 8(B)
// / \
// 6(B)
//
// 插入后:
// 7(B)
// / \
// 5(R) 8(B)
// / \
// 3(R) 6(B)
//
// 右旋后:
// 5(B)
// / \
// 3(R) 7(R)
// / \
// 6(B) 8(B)
//
// * 插入到3-Node类型节点的中侧
// 最后一种插入情况了,放最后是因为这种情况最麻烦
// 如示例所示,将6插入到3-Node类型节点的中侧,插入后,新节点为红色,
// 不满足红黑树中右链接不能出现红色的特性,此时将5节点进行左旋转,旋转
// 后仔细观察,其中这时候出现左节点、以及左节点的左节点为红色,这个现象
// 同之前的"插入到3-Node类型节点的左侧"的相同了,所以采用那种情况的解决
// 方法,将当前节点7再进行一次右旋转,这时候又出现了左、右子节点都为红
// 色的现象,采用之前的方法,将两个子节点变成黑色,子树的根节点变成红
// 色。
//
// 插入前:
// 7(B)
// / \
// 5(R) 8(B)
// / \
// 3(B)
//
// 插入后:
// 7(B)
// / \
// 5(R) 8(B)
// / \
// 3(B) 6(R)
//
// 对5节点进行左旋后:
// 7(B)
// / \
// 6(R) 8(B)
// /
// 5(R)
// /
// 3(B)
//
// 对7节点进行右旋后:
// 6(B)
// / \
// 5(R) 7(R)
// / \
// 3(B) 8(B)
//
public override void Put(TKey key, TValue value)
{
root = Put(root, key, value);
root.Color = BLACK;
}
private Node Put(Node h, TKey key, TValue value)
{
if (h == null) return new Node(key, value, 1, RED);
int cmp = key.CompareTo(h.Key);
if (cmp < 0) h.Left = Put(h.Left, key, value);
else if (cmp > 0) h.Right = Put(h.Right, key, value);
else h.Value = value;
//平衡化操作
if (IsRed(h.Right) && !IsRed(h.Left)) h = RotateLeft(h);
if (IsRed(h.Right) && IsRed(h.Left.Left)) h = RotateRight(h);
if (IsRed(h.Left) && IsRed(h.Right)) h = FlipColor(h);
h.Number = Size(h.Left) + Size(h.Right) + 1;
return h;
}
private int Size(Node node)
{
if (node == null) return 0;
return node.Number;
}
//查找
//这里同普通二叉树查找算法相同,不再进行描述
//查找获取指定的值
public override TValue Get(TKey key)
{
return GetValue(root, key);
}
private TValue GetValue(Node node, TKey key)
{
if (node == null) return default(TValue);
int cmp = key.CompareTo(node.Key);
if (cmp == 0) return node.Value;
else if (cmp > 0) return GetValue(node.Right, key);
else return GetValue(node.Left, key);
}
如果上面概念不是很清楚,再上几张图片:
左旋:
右旋:
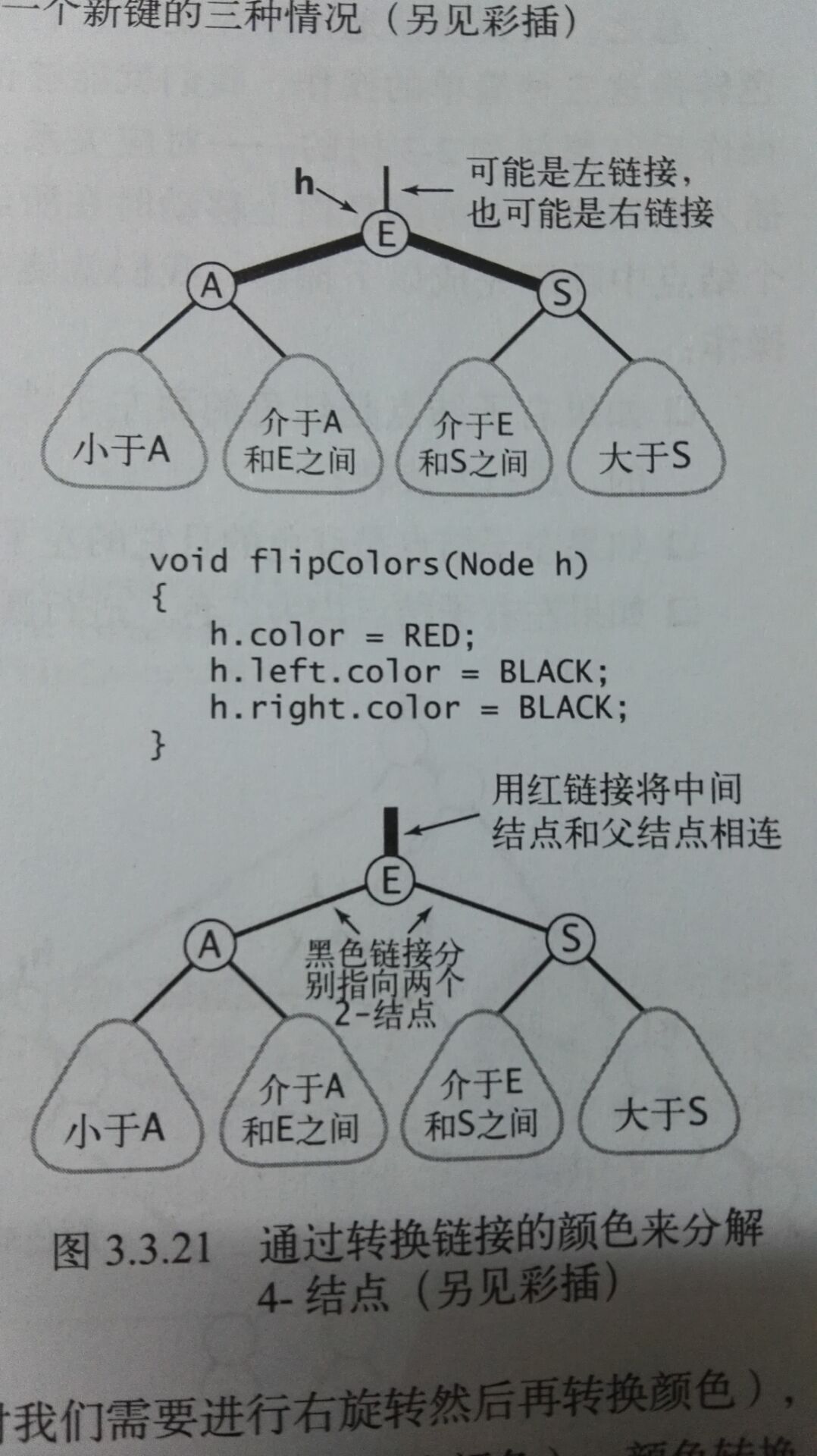
flipColors:
参考:
http://www.cnblogs.com/yangecnu/p/Introduce-Red-Black-Tree.html
http://blog.csdn.net/liujianfeng1984/article/details/47378715


























 3388
3388

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








