二叉树笔记

性质：

1.在二叉树的第i层上最多有2^i-1(i>=1，2的i-1次方)
2.深(高)度为k的二叉树最多有2^k-1个结点(k>=1，2的k次方-1)
3.对任何一棵二叉树，如果度为0的结点数(叶子结点数)为n0,度为2的结点数为n2,则n0=n2+1 (由总结点数=树的总度数+1可证)
4.具有n个结点的完全二叉树的深度为|_log2n_|+1
5.如果对一棵有n个结点的完全二叉树的结点按层序编号(从第1层到|_long2n_|+1层，每层从左到右),则对任一结点i(1<=i<=n),有：
               如果i=1,则结点i无父结点，是二叉树的根；如果i>1，则父结点是|_i/2_|；
               如果2i>n，则结点i为叶子结点，无左子结点；否则，其左子结点是结点2i;
               如果2i+1>n，则结点i无右子结点；否则，其右子结点是结点2i+1。

遍历：

先序遍历：根－左－右
中序遍历：左－根－右
后序遍历：左－右－根

树转二叉树：

树的先序遍历＝二叉树的先序遍历
树的中序遍历!=二叉树的中序遍历
树的后序遍历＝二叉树的中序遍历

如何构造赫夫曼树：

                (1)根据给定的n个权值{w1,w2,...,wn}构成n棵二叉树的集合F＝{T1,T2，…，
                   Tn}，其中每棵二叉树Ti中只有一个带权为wi的根结点，其左右子树均空。

                (2)在F中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树．
                   且新的二叉树的根结点权值为其左、右子树上根结点的权值之和。

                (3)在F中删除这两棵树，同时将新得到的二叉树加入F中

                (4)重复(2)和(3)，直到F只含一棵树为止，这棵树便是赫夫曼树。

习题1：

             若一棵赫夫曼树共有9个顶点，则其叶子节点的个数为多少？
  
             解：
                因为：赫夫曼树的构造过程是每权值小的结点产生一个新的根结点
                所以：从赫夫曼树的构造特征可知一个根结点要么就是有左右孩子
                      要不就无孩子(叶子)
                所以：赫夫慢树的总顶点(结点)数＝叶子结点数+度为2的结点数
                又因为：由前面提到的二叉树的性质3 n0=n2+1
                所以：总顶点数(9)=n0+n2
                即：总顶点数(9)=n2+1+n2
                所以：n2=4
                所以：n0=5
     
                因此此赫夫曼树的叶子节点的个数为是5

查找二叉树(二叉排序树)的性质:
          二叉排序树或者是一棵空树,或者是一棵具有如下性质的二叉树：
          1.若它的左子树非空，则左子树上所有结点的值均小于根结点的值；
          2.若它的右子树非空，则右子树上所有结点的值均大于根结点的值；
          3.左、右子树本身又各是一棵二叉排序树。
          4.按中序遍历二叉排序树，所得到的中序遍历序列是一个递增有序序列。

查找二叉树(二叉排序树)的结点插入操作:

1.如果相同键值的结点已在查找二叉树中，则不再插入；
2.如果查找二叉树为空树,则以新结点为查找二叉树;
3.将要插入结点的键值与插入后的父结点的键值比较(小于父结点则置左否则置右),就能确定新
         结点是父结点的左子结点还是右子结点,并进行相应插入.

查找二叉树(二叉排序树)的结点删除操作:

1.若待删除的节点p是叶子节点,则直接删除该节点;
2.若待删除的节点p只有一个子节点,则将这个子节点w与待删除节点的父节点直接连接,然后删除节点p
         若子节点w下还有子节点则也同样上移,也就是说将w为根的整棵树都向上移一层;
3.若待删除的节点p有两个子节点,则在其左子树上,用中序遍历寻找关键值最大的节点s,用节点s的值代
         替节点p的值,然后删除节点s,节点s必属于上述1和2情况之一(由性质4可知)  

关于线索二叉树:

    因为普通二叉树的结点存储结构为:|Lchild|Data|Rchild|
    而叶子结点的Lchild和Rchild均为NULL指针,因此乱费了存储空间,
    设总结点数为n,则只有n-1个指针指向了有用的结点,而有
    n+1个指针指向了NULL指针,因此乱费了n+1个指针所占用的存储空间,
    为了节省空间可将其n+1个指针域指向实际的结点的前驱和后继指针
    为此产生了新的存储结构为:|Lbit|Lchild|Data|Rchild|Rbit|其中
    Lbit和Rbit分别是逻辑型数据只存0或1,虽然每个结点都新增了Lbit
    和Rbit域,但是因为其是逻辑型数据所以每个节点只比普通存储结构多
    占用了两个位的存储空间,相比乱费了n+1个指针域所占的存储空间来
    说是更加理想的.如果Lbit=0则说明Lchild是指向了结点的左孩子(或左
    子树)的指针,如为1则说明Lchild是指向结点的前趋的左线索,Rbit也同
    理.这样普通的二叉树就可按一种顺序转变成为了线索二叉树了,这样就
    可更方便的随机的查找指定结点的前驱和后继了,而这种顺序可以是按先
    序遍历,中序遍历,后序遍历三种之一形成的顺序.

普通二叉树线索化:
  
    先序线索化:先按先序遍历写出普通二叉树的编号序列S={si-1,si,si+1...sn}(i是正整数)
              其中si的前驱是si-1,后继是si+1然后根据结点的Lbit和Rbit来决定是用普通线
              还是用线索连接(0表示指向左或右孩子结点的普通线,1表示指向前驱或后继的
              线索线)用不带箭头的实线表示普通线,带箭头的实线来表示前驱线索线,用带箭头的
              虚线表示后继线索线.然后根据序列S用这两种线索线连接好各结点,则形成了以先序
              遍历为顺序的线索二叉树
    中序线索化: 同理
    后序线索化: 同理

查找指定线索二叉树中指定结点的前驱或后继
现举例在后序线索树中找结点后继,其他两种
线索二叉树根据其遍历规律可类推:
  
    分为三种情况(后序线索):
      (注意的是,普通二叉树线索化后,其中有可能存在结点与其前驱或与其后继间无任何直接
      的连线,此时用以下方法获得,当然有带箭头连线(即线索线)的结点找前驱和后继很简单)
      1.若结点x是二叉树的根,则其后继为NULL(因为后序是: 左右根);
      2.若结点x是其双亲的右孩子(即x的父亲的Rbit=0)或者左孩子(即x的父亲的Lbit=0)且
        其父亲没有右孩子,则其后继即为父亲结点;
      3.若结点x是其父亲的左孩子且其父亲有右子树,则其后继为父亲的右子树
        上按后序遍历列出的第一个结点.
             
线索二叉树的实质:
    
      对一个非线性结构的普通二叉树进行线性操作,使每个结点(除第一个和最后一个外)在这些
      线性序列中有且仅有一个直接前驱和直接后继,从而实现了随机方便的查找某一结点的前驱和后继
      按某种次序将二叉树线索化的实质是：按该次序遍历二叉树，在遍历过程中用线索取代空指针。
  

平衡二叉树(Balanced Binary Tree)的定义:

      或者是一棵空树,或者是一棵这样的树:树中任一结点的左、右子树的深度之差的绝对值不超过1.
      注意:是树中任一结点,所以不能凭视觉判断一棵二叉树是否是平衡二叉树.
      如定义结点的平衡度为两左、右子树深度的差值,则对于平衡二叉树,它的每个结点的平
      衡度只能为-1,0,1三个值之一.

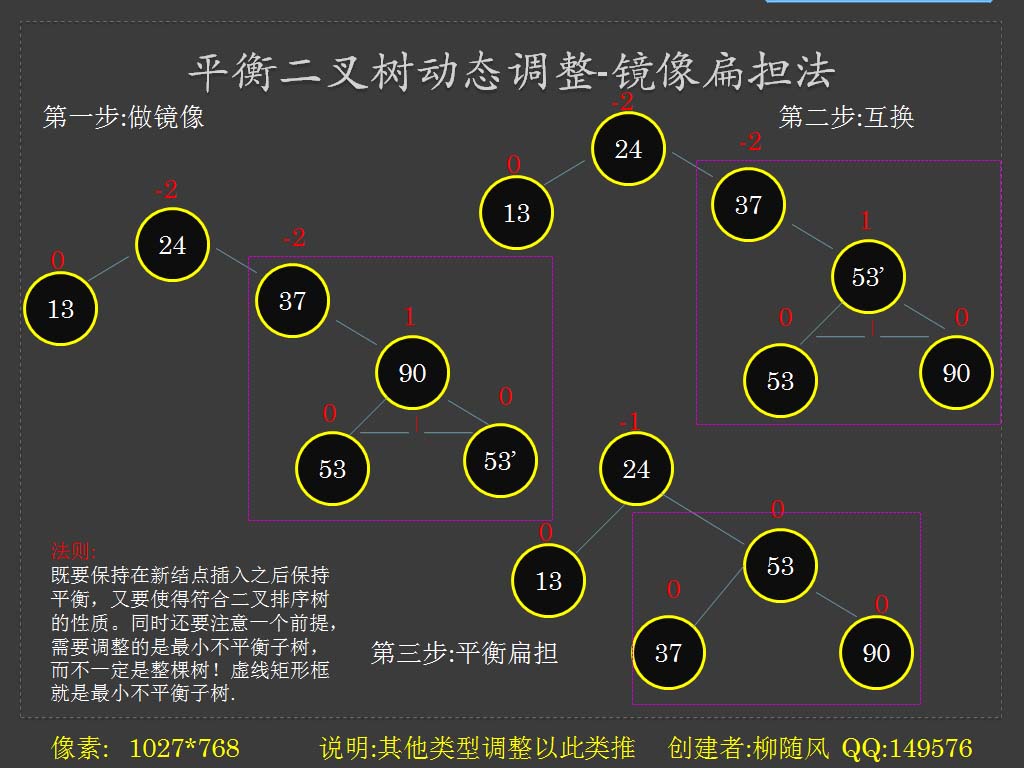
平衡树的调整:

      法则:
      首先要明白，在插入新结点做平衡二叉树调整时，前提是这棵树既是平衡二叉树又必须是二叉
      排序树，因此调整的指导原则是：既要保持在新结点插入之后保持平衡，又要使得符合二叉排
      序树的性质。同时还要注意一个前提，需要调整的是最小不平衡子树，而不一定是整棵树！
      实现:
           用柳随风[87年的老纳的前身]‘发明’的"镜像扁担法"^_^，