矩阵乘法(矩阵乘矩阵)
在向量乘向量的运算中,是将每个元素与它对应的元素相乘,求所有乘积之和
那么矩阵乘矩阵是不是就是两个同型矩阵的对应元素相乘呢?
图样图森破
两个矩阵相乘的前提是前一个矩阵的列数等于后一个矩阵的行数
举个栗子,AAA为n∗kn*kn∗k矩阵,BBB为k∗mk*mk∗m矩阵,CCC为m∗nm*nm∗n矩阵,那么AAA可以与BBB相乘,BBB可以与CCC相乘,CCC可以与AAA相乘,其他均不成立
我们知道了什么情况下两个矩阵可以相乘,那么他们怎么相乘呢?不讲每个对应位置相乘还能怎么乘呢?
设AAA为n∗kn*kn∗k矩阵,BBB为k∗mk*mk∗m矩阵,那么它们的乘积CCC则为一个n∗mn*mn∗m矩阵
Ci,j=∑r=1kAi,r∗Br,jC_{i,j}=\sum_{r=1}^kA_{i,r}*B_{r,j}Ci,j=∑r=1kAi,r∗Br,j
是不是不太好理解,没关系看看图就知道了

在矩阵乘法中满足以下运算律:
(AB)C=a(BC)(AB)C=a(BC)(AB)C=a(BC)
(A+B)C=AC+BC(A+B)C=AC+BC(A+B)C=AC+BC
C(A+B)=CA+CBC(A+B)=CA+CBC(A+B)=CA+CB
了解了这么多,我们开始看题,矩阵快速幂,由于矩阵乘法满足结合律,所以我们只需要把它按照一般的快速幂打,再重载一下运算符就可以了,好了我们直接放一道模板题:
题目描述
给定n*n的矩阵A,求A^k
输入输出格式
输入格式:
第一行,n,k
第2至n+1行,每行n个数,第i+1行第j个数表示矩阵第i行第j列的元素
输出格式:
输出A^k
共n行,每行n个数,第i行第j个数表示矩阵第i行第j列的元素,每个元素模10^9+7
输入输出样例
输入样例#1: 复制
2 1
1 1
1 1输出样例#1: 复制
1 1
1 1说明
n<=100, k<=10^12, |矩阵元素|<=1000
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#define MOD 1000000007
using namespace std;
typedef long long int ll;
struct mat
{
ll a[105][105];
}ans,res;//用二维数组来存储矩阵
ll k;
ll n;
mat Mul(mat x,mat y,ll n)//定义矩阵乘法,其中n是矩阵的阶数
{
mat t;//用来存储乘完之后的结果
memset(t.a,0,sizeof(t.a));
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
{
for(int k=0;k<n;k++)
{
t.a[i][j]+=x.a[i][k]*y.a[k][j];
t.a[i][j]%=MOD;
}
}
return t;
}
void quickMod(ll N,ll n)//N是求幂的次数,n是阶数
{
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
if(i==j)
ans.a[i][j]=1;
else
{
ans.a[i][j]=0;
}
}
}//这个过程是求单位矩阵的过程,类似于矩阵快速幂里面的ans=1;
while(N)
{
if(N&1)
{
ans=Mul(ans,res,n);//矩阵乘法不满足交换律,切记
}
N>>=1;
res=Mul(res,res,n);
}
}
int main()
{
scanf("%lld%lld",&n,&k);
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
scanf("%lld",&res.a[i][j]);
}
}//相当于把第一个矩阵赋初值
quickMod(k,n);
for(int i=0;i<n;i++)//输出矩阵的过程
{
for(int j=0;j<n;j++)
{ if(j==0)
printf("%lld",ans.a[i][j]);
else
printf(" %lld",ans.a[i][j]);
}
printf("\n");
}
return 0;
}想必大家对于矩阵快速幂有了一定的了解,那么矩阵快速幂可以用了做什么呢?
可以去求解递推式的问题,比如斐波那契数列
下列就附上求解斐波那契数列的代码:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#define MOD 1000000007
using namespace std;
typedef long long int ll;
struct mat
{
ll a[4][4];
}ans,res;
mat Mul(mat x,mat y)
{
mat t;
memset(t.a,0,sizeof(t.a));
for(int i=0;i<2;i++)
{
for(int j=0;j<2;j++)
{
for(int k=0;k<2;k++)
{
t.a[i][j]+=(x.a[i][k]*y.a[k][j]);
t.a[i][j]%=(MOD-1);
}
}
}
return t;
}
void quickMod(long long int N)
{
ans.a[0][0]=1;
ans.a[0][1]=0;
ans.a[1][0]=0;
ans.a[1][0]=1;
while(N)
{
if(N&1)
{
ans=Mul(ans,res);
}
res=Mul(res,res);
N>>=1;
}
}
int main()
{
ll n;
while(scanf("%lld",&n)!=EOF)
{
res.a[0][0]=1;
res.a[0][1]=1;
res.a[1][0]=1;
res.a[1][1]=0;
quickMod(n);
printf("%lld\n",ans.a[0][0]);
}
return 0;
} 斐波那契数列还有很多变式(摘自杨紫陌学长的博客,链接https://www.cnblogs.com/yzm10/
矩阵快速幂求long long级斐波那契(变形)。
f[n]=a*f[n-1]+b*f[n-2], f[1]=a1,f[2]=a2, MOD=...
由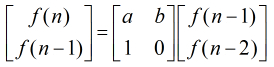
其他变形:
1.f(n)=a*f(n-1)+b*f(n-2)+c;(a,b,c是常数)
2.f(n)=c^n-f(n-1) ;(c是常数)








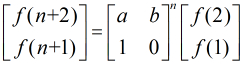

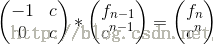















 1853
1853











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










