主要内容包括:
1.Anaconda软件的安装过程及简单配置
2.聚类及Kmeans算法介绍
3.案例分析:Kmeans实现运动员位置聚集
前文推荐:【Python数据挖掘课程】一.安装Python及爬虫入门介绍
希望这篇文章对你有所帮助,尤其是刚刚接触数据挖掘以及大数据的同学,同时准备尝试以案例为主的方式进行讲解。如果文章中存在不足或错误的地方,还请海涵~
一. Anaconda软件安装及使用步骤
前面两节课我是通过Python命令行和IDLE工具进行介绍的,但是里面的配置比较麻烦,包括pip安装,selenium、lda各种第三方包的安装。
从这节课我准备使用Anacaonda软件来讲解,它集成了各种Python的第三方包,尤其包括数据挖掘和数据分析常用的几个包。
下载地址:https://www.continuum.io/downloads/
云盘分享:http://pan.baidu.com/s/1hrEQ9xi
1. 配置过程
首先简单介绍安装过程以及如何使用。
安装Anaconda
安装过程如下所示:
安装最好在C盘默认路径下(空间不大,方便配置),同时不要使用中文路径。
安装完成后,点击“Finish”。点击Anaconda文件夹,包括这些exe执行文件:
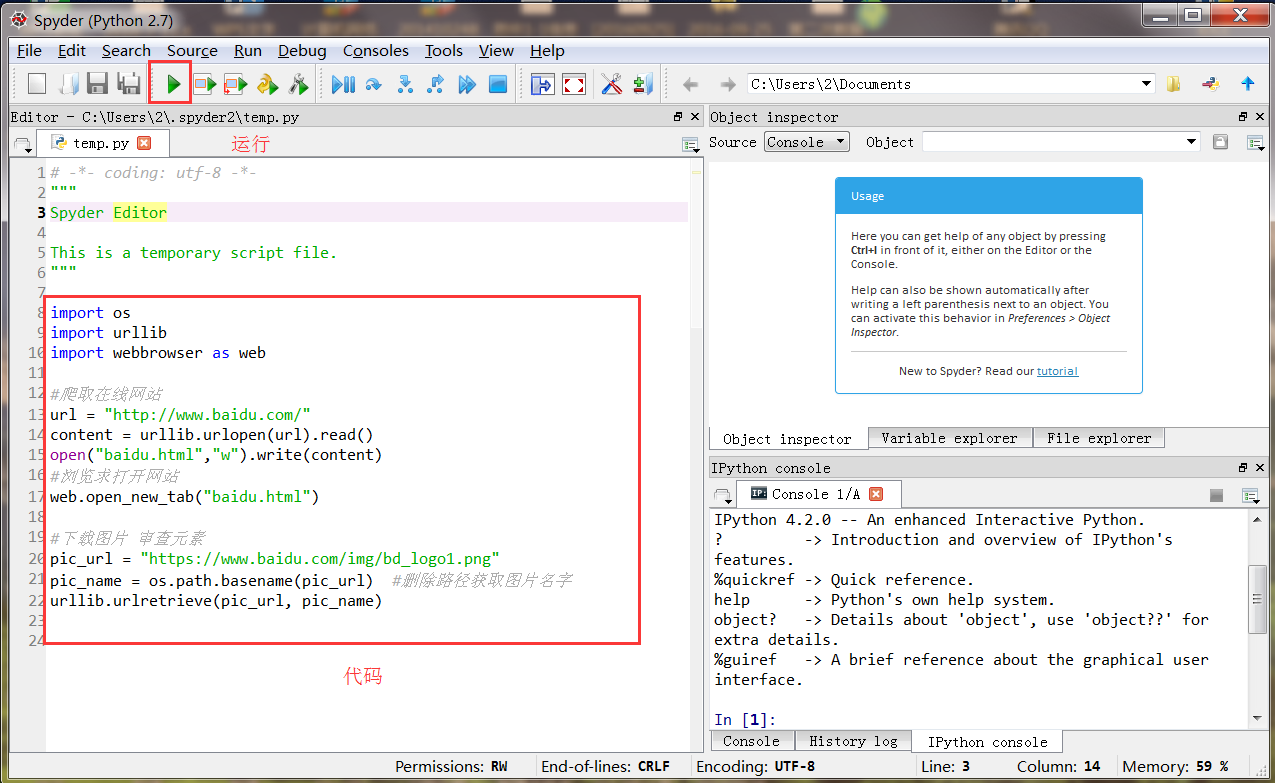
这里我们使用Spyder进行编写Python程序。运行如下所示,左边是进行代码编写的,右下角Console是输出结果的地方。
安装第三方包
虽然Anaconda软件集成了各种各样的包,但是还是缺少一些第三方包,需要通过调用pip或easy_install命令进行安装。
然后使用cd ..去到C盘根目录,cd去到Anaconda的Scripts目录下,输入"pip install selenium"安装selenium相应的包,"pip install lda"安装lda包。
2. 机器学习常用包
下面这四个包通常用于Python数据挖掘和大数据分析的,包括:
Scikit-Learn
Scikit-Learn是一个基于python的用于数据挖掘和数据分析的简单且有效的工具,它的基本功能主要被分为六个部分:分类(Classification)、回归(Regression)、聚类(Clustering)、数据降维(Dimensionality Reduction)、模型选择(Model Selection)、数据预处理(Preprocessing)。
详见官网:http://scikit-learn.org/stable/
NumPy
NumPy(Numeric Python)系统是Python的一种开源的数值计算扩展,一个用python实现的科学计算包。它提供了许多高级的数值编程工具,如:矩阵数据类型、矢量处理,以及精密的运算库。专为进行严格的数字处理而产生。
SciPy
SciPy (pronounced "Sigh Pie") 是一个开源的数学、科学和工程计算包。它是一款方便、易于使用、专为科学和工程设计的Python工具包,包括统计、优化、整合、线性代数模块、傅里叶变换、信号和图像处理、常微分方程求解器等等。
Matplotlib
Matplotlib是一个Python的图形框架,类似于MATLAB和R语言。它是python最著名的绘图库,它提供了一整套和matlab相似的命令API,十分适合交互式地进行制图。而且也可以方便地将它作为绘图控件,嵌入GUI应用程序中。
二. 聚类及Kmeans介绍
这部分内容主要简单介绍聚类的原理及Kmeans相关知识。
机器学习的基本思想,我还是介绍下面这张图,非常经典。
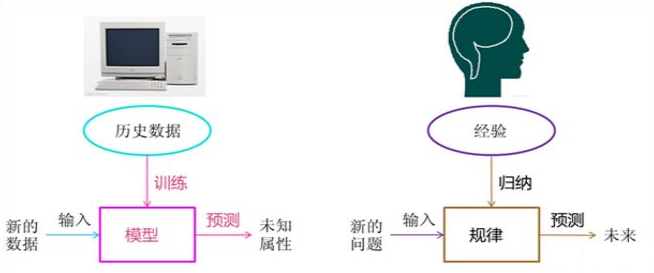
这里讲述聚类的部分,我简单推荐"简书-程sir"的文章,简单易懂,很不错。
推荐地址:http://www.jianshu.com/p/fc91fed8c77b
1. 分类与聚类
聚类
俗话说“物以类聚”,其实从广义上说,聚类就是将数据集中在某些方面相似的数据成员放在一起。一个聚类就是一些数据实例的集合,其中处于相同聚类中的数据元素彼此相似,但是处于不同聚类中的元素彼此不同。
由于在聚类中那些表示数据类别的分类或分组信息是没有的,即这些数据是没有标签的,所有聚类及时通常被成为无监督学习(Unsupervised Learning)。
下图是800篇文章,每个点可以看成一篇文章,然后对文本进行聚类分析,可以看到相同主题的文章是聚集在一起的。总共四个主题,红色表示景区Spot、蓝色表示人物People、黑色表示国家Country、绿色表示动物Animal。
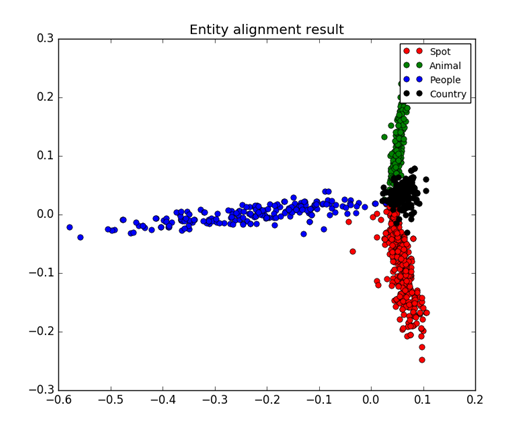
分类
在理解聚类之前,必须要先理解聚类和分类的区别,简单举个例子。
分类其实是从特定的数据中挖掘模式,作出判断的过程。比如Gmail邮箱里有垃圾邮件分类器,一开始的时候可能什么都不过滤,在日常使用过程中,我人工对于每一封邮件点选“垃圾”或“不是垃圾”,过一段时间,Gmail就体现出一定的智能,能够自动过滤掉一些垃圾邮件了。
这是因为在点选的过程中,其实是给每一条邮件打了一个“标签”,这个标签只有两个值,要么是“垃圾”,要么“不是垃圾”,Gmail就会不断研究哪些特点的邮件是垃圾,哪些特点的不是垃圾,形成一些判别的模式,这样当一封信的邮件到来,就可以自动把邮件分到“垃圾”和“不是垃圾”这两个我们人工设定的分类的其中一个。
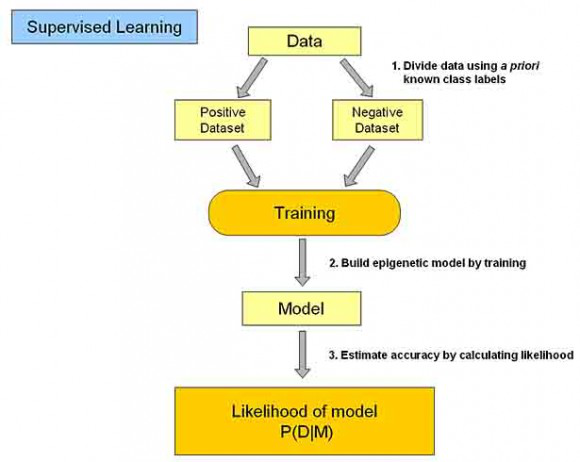
(1)训练数据集存在一个类标记号,判断它是正向数据集(起积极作用,不垃圾邮件),还是负向数据集(起抑制作用,垃圾邮件);
(2)然后需要对数据集进行学习训练,并构建一个训练的模型;
(3)通过该模型对预测数据集进预测,并计算其结果的性能。
聚类的的目的也是把数据分类,但是事先我是不知道如何去分的,完全是算法自己来判断各条数据之间的相似性,相似的就放在一起。在聚类的结论出来之前,我完全不知道每一类有什么特点,一定要根据聚类的结果通过人的经验来分析,看看聚成的这一类大概有什么特点。
总之,聚类主要是"物以类聚",通过相似性把相似元素聚集在一起,它没有标签;而分类通过标签来训练得到一个模型,对新数据集进行预测的过程,其数据存在标签的。
2. Kmeans算法
该部分转载简书-程sir的文章:聚类、K-Means、例子、细节
K-Means是聚类算法中的最常用的一种,算法最大的特点是简单,好理解,运算速度快,但是只能应用于连续型的数据,并且一定要在聚类前需要手工指定要分成几类。
下面,我们描述一下K-means算法的过程,为了尽量不用数学符号,所以描述的不是很严谨,大概就是这个意思,“物以类聚、人以群分”:
1、首先输入k的值,即我们希望将数据集经过聚类得到k个分组。
2、从数据集中随机选择k个数据点作为初始大哥(质心,Centroid)
3、对集合中每一个小弟,计算与每一个大哥的距离(距离的含义后面会讲),离哪个大哥距离近,就跟定哪个大哥。
4、这时每一个大哥手下都聚集了一票小弟,这时候召开人民代表大会,每一群选出新的大哥(其实是通过算法选出新的质心)。
5、如果新大哥和老大哥之间的距离小于某一个设置的阈值(表示重新计算的质心的位置变化不大,趋于稳定,或者说收敛),可以认为我们进行的聚类已经达到期望的结果,算法终止。
6、如果新大哥和老大哥距离变化很大,需要迭代3~5步骤。
下面这个例子很好的,真心推荐大家学习他的博客。
他搞了6个点,从图上看应该分成两推儿,前三个点一堆儿,后三个点是另一堆儿。现在手工执行K-Means,体会一下过程,同时看看结果是不是和预期一致。
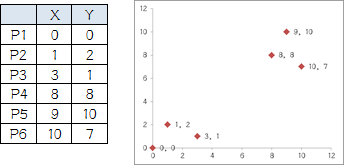
1.选择初始大哥:
我们就选P1和P2
2.计算小弟和大哥的距离:
P3到P1的距离从图上也能看出来(勾股定理),是√10 = 3.16;P3到P2的距离√((3-1)^2+(1-2)^2 = √5 = 2.24,所以P3离P2更近,P3就跟P2混。同理,P4、P5、P6也这么算,如下:
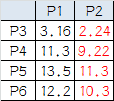
P3到P6都跟P2更近,所以第一次站队的结果是:
• 组A:P1
• 组B:P2、P3、P4、P5、P6
3.人民代表大会:
组A没啥可选的,大哥还是P1自己
组B有五个人,需要选新大哥,这里要注意选大哥的方法是每个人X坐标的平均值和Y坐标的平均值组成的新的点,为新大哥,也就是说这个大哥是“虚拟的”。
因此,B组选出新大哥的坐标为:P哥((1+3+8+9+10)/5,(2+1+8+10+7)/5)=(6.2,5.6)。
综合两组,新大哥为P1(0,0),P哥(6.2,5.6),而P2-P6重新成为小弟。
4.再次计算小弟到大哥的距离:
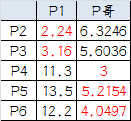
这时可以看到P2、P3离P1更近,P4、P5、P6离P哥更近,第二次站队的结果是:
• 组A:P1、P2、P3
• 组B:P4、P5、P6(虚拟大哥这时候消失)
5.第二届人民代表大会:
按照上一届大会的方法选出两个新的虚拟大哥:P哥1(1.33,1) P哥2(9,8.33),P1-P6都成为小弟。
6.第三次计算小弟到大哥的距离:
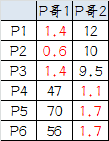
这时可以看到P1、P2、P3离P哥1更近,P4、P5、P6离P哥2更近,所以第二次站队的结果是:
• 组A:P1、P2、P3
• 组B:P4、P5、P6
我们发现,这次站队的结果和上次没有任何变化了,说明已经收敛,聚类结束,聚类结果和我们最开始设想的结果完全一致。
三. 案例分析:Kmeans聚类运动员数据
1. 数据集
现在存在下面的数据集,是篮球球员比赛的数据。
数据集地址:KEEL-dataset - Basketball data set
该数据集主要包括5个特征(Features),共96行数据。

特征描述:共5个特征,每分钟助攻数、运动员身高、运动员出场时间、运动员年龄和每分钟得分数。

需求:现在需要通过运动员的数据,判断他是什么位置。
如果某些运动员得分高,他可能是得分后卫;如果某些运动员身高高或篮板多,他可能是中锋;助攻高可能是控卫。
2. 代码
这里我仅仅使用两列数据,助攻数和得分数进行实验,相当于20*2的矩阵,其中输出y_pred结果表示聚类的类标。类簇数设置为3,类标位0、1、2,它也是与20个球员数据一一对应的。
Sklearn机器学习包中导入了KMeans聚类,同时需要注意Matplotlib包绘制图形的过程。代码如下,并包括详细注释:
聚类核心代码:
from sklearn.cluster import KMeans
clf = KMeans(n_clusters=3)
y_pred = clf.fit_predict(X)
绘图核心代码:
import matplotlib.pyplot as plt
plt.scatter(x, y, c=y_pred, marker='x')
plt.title("Kmeans-Basketball Data")
plt.xlabel("assists_per_minute")
plt.ylabel("points_per_minute")
plt.show()
3. 运行结果
运行结果如下所示:
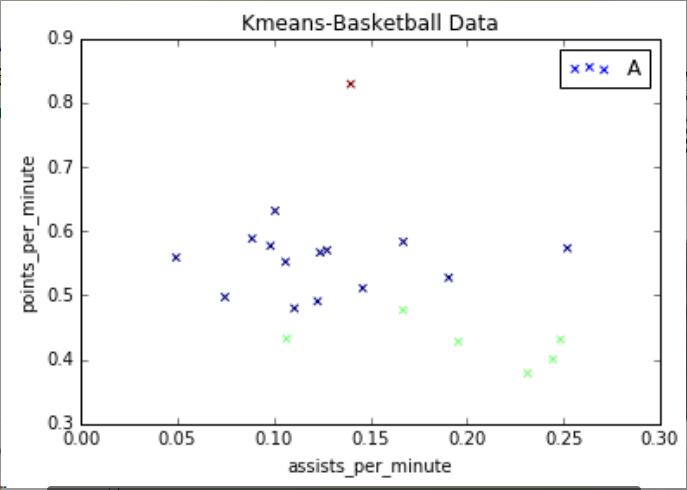
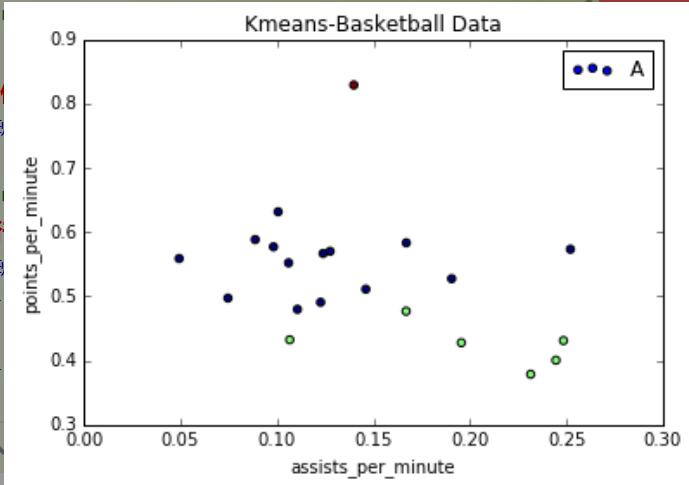
如果设置marker='o',输出圆形,可以看到红色点很高,他得分和助攻都比较高,相当于篮球里面的"乔丹",然后中间一部分,右下角一部分助攻很高、得分低,可能是控卫。当然数据集越多,聚类的效果越好。
常见问题:
1、安装Anaconda不能使用中文路径,以及电脑名称为中文;
2、Spyder如何显示中文,而不是"口口口"乱码,需要改Fonts;
3、Matplotlib如何显示颜色,定义样式等;
4、如何读取数据,赋值给变量,在让其显示。
希望这篇文章对你有所帮助,主要是介绍一个基于Python的Kmeans聚类案例,后面会陆续详细介绍各种知识。非常想上好这门课,因为是我的专业方向,另外学生们真的好棒,好认真,用手机录像、问问题、配环境等等,只要有用心的学生,我定不负你!同时,这节课的思路好点了,摸着石头过马路,需要慢慢学吧,但还是挺享受的,毕竟9800,哈哈哈!
(By:Eastmount 2016-10-10 晚上10点 http://blog.csdn.net/eastmount/ )
最后提供篮球的完整数据集:






















 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








